3.1圆 课件(共22张PPT)
图片预览





文档简介
(共22张PPT)
§3.1 圆
北师版九年级下册 圆
1.知道圆的有关定义及表示方法;
2.掌握点和圆的位置关系;
3.会根据要求画出图形.
如图3-1,一些学生正在做投圈游戏、他们的投圈标都是图中的花瓶。如果他们呈"一"字排开,这样的队形对每个人都公平吗 你认为他们应当排成什么样的队形才公平
图3-1
解:不公平.因为圆上任意一点到圆心的距离是相等的,因而排成圆形才能对每个人公平.
若想游戏公平,应排成圆形.
情景导入
如果现在有一条3米长的绳子, 你准备怎么办
小贴士
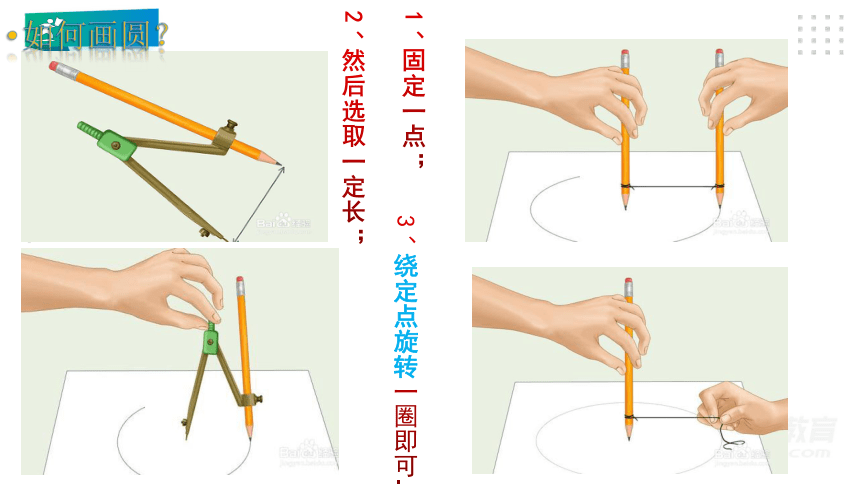
如何画圆?
1、固定一点;
2、然后选取一定长;
3、绕定点旋转一圈即可.
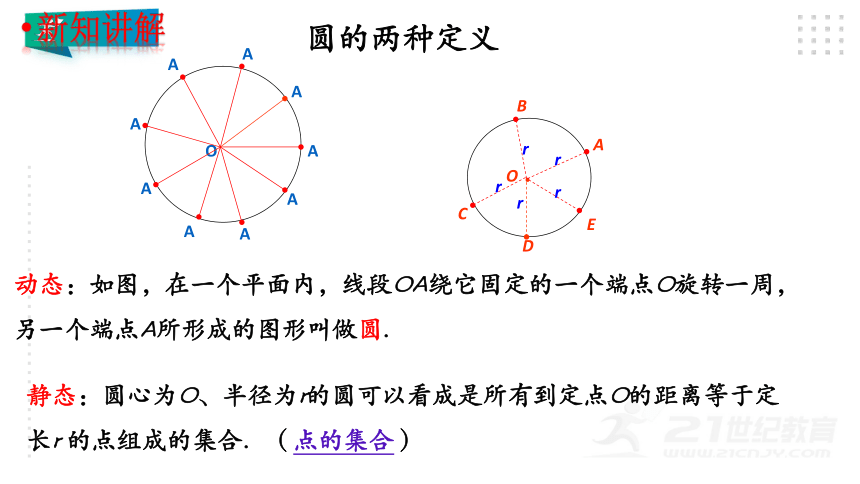
动态:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的集合.(点的集合)
O
A
A
A
A
A
A
A
A
A
O
·
A
B
C
D
E
r
r
r
r
r
圆的两种定义
新知讲解
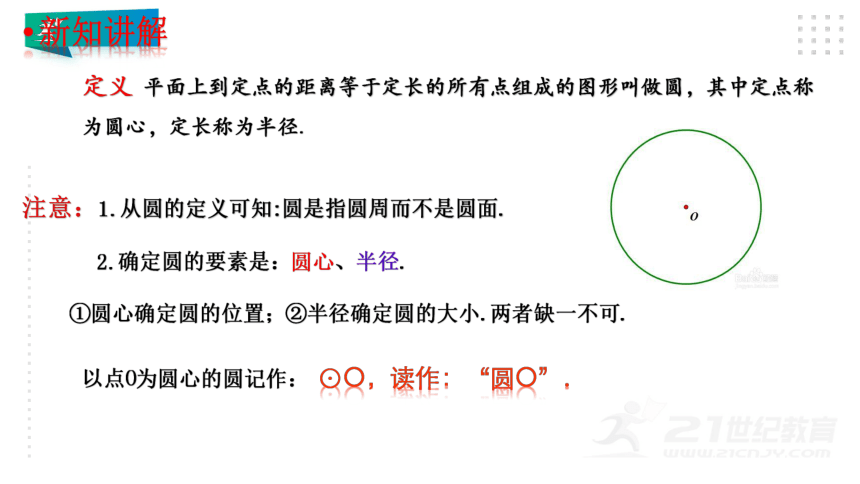
定义 平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点称为圆心,定长称为半径.
以点O为圆心的圆记作:
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.
①圆心确定圆的位置;②半径确定圆的大小.两者缺一不可.
⊙O,读作:“圆O”.
新知讲解
Add Text
点击此处添加标题
集合思想
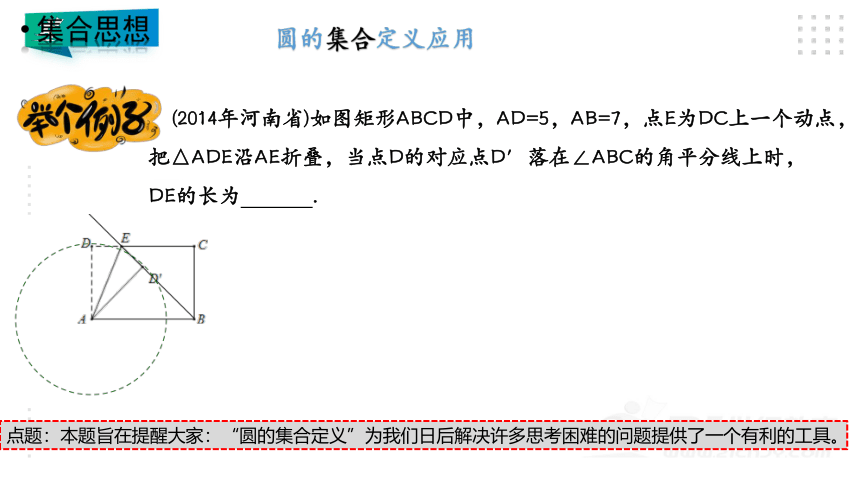
圆的集合定义应用
(2014年河南省)如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,
把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,
DE的长为 .
点题:本题旨在提醒大家:“圆的集合定义”为我们日后解决许多思考困难的问题提供了一个有利的工具。
除圆心、半径以外,还有:
如图3-2,连接圆上任意两点的线段叫做弦(chord),
如 AB;经过圆心的弦叫做直径(dianneter),如CD.
我们知道,圆上任意两点间的部分叫做圆弧
圆的任意一条直经的两个端点分圆成两条弧,每一条弧都叫做半圆
(semicircle ).
能够重合的两个圆叫做等圆(equal circles ).在同图3-2
圆或等圆中,能够互相重合的弧叫做等弧(equal arcs).
新知讲解
圆的基本元素
图3-2
跟踪练习
1、如图,AB是⊙O的直径,C点在⊙O上,那么,哪一段弧是优弧,哪一段弧是劣弧?
2 判断下列说法是否正确
(1)直径是弦.( );(2)弦是直径.( )
(3)半圆是弧.( );(4)弧是半圆.( )
(5)长度相等的两段弧是等弧.( )
(6)等弧的长度相等.( )
(7)两个劣弧之和等于半圆.( )
(8)半径相等的两个半圆是等弧.( )
√
×
√
×
×
√
√
×
点与圆的位置关系
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么
若点A在⊙O内
若点A在⊙O上
若点A在⊙O外
OA<r, OB=r, OC>r.
反过来也成立,即
结论:点的位置可以确定该点到圆心的距离与半径的关系,
反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
新知讲解
设 AB=3 cm,画图说明满足下列要求的图形∶
(1)到点A和点B的距离都等于2cm 的所有点组成的图形;
(2)到点A和点B的距离都小于2cm的所有点组成的图形、
2.小明和小华正在练习投铅球,樊球场地分为五个区域∶4m以内,4~5m,5~6m,6~7m,7m以外.小明投了5.2m,小华投了6.7m,他们投的球分别落在哪个区域内
跟踪练习
解:如图,点C、D即是符合(1)要求的图形;
图中所涂阴影部分即是符合(2)要求的图形.
解:小明投在了5~6m的区域;小华投在了6~7m的区域.
1.下列说法正确的是( )
A.半圆是弧,弧也是半圆
B.过圆上任意一点只能作一条弦,且这条弦是直径
C.弦是直径
D.直径是圆中最长的弦
D
课堂练习
2.下列条件中,能画唯一圆的是( )
A.以已知点O为圆心
B.以点O为圆心,2 cm长为半径
C.以1 cm长为半径
D.经过已知点A,且半径为2 cm
B
课堂练习
3.(2020·安阳林州期末)已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上
C.点P在圆外 D.不能确定
A
课堂练习
4.已知⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
A
课堂练习
5.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=3=r,∴点B在⊙C上.
课堂练习
6.下列命题,其中正确的有( )
①两个端点能够重合的弧是等弧;②面积相等的两个圆是等圆;③弦是圆上任意两点之间的部分;④同圆或等圆中,劣弧比优弧短.
A.1个 B.2个 C.3个 D.4个
B
课堂练习
7.(2020·烟台)量角器测角度时摆放的位置如图所示,在△AOB中,
射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70°
C.80° D.85°
C
课堂练习
C
8.(2019·聊城)如图,BC是半圆O的直径,D,E是BC上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35° B.38°
C.40° D.42°
︵
点题:解决本题的关键是“牢记同圆的半径处处相等”,从而结合等腰三角形的知识解题
课堂练习
9.如图,小虎牵着小狗上街,小虎的手臂与绳共2.5 m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
解:小狗在地面上环绕的圆的半径为r=2(m),
S=πr2=4π(m2),
故小狗在平整的地面上活动的最大区域是以小虎为圆心,2 m长为半径的圆,其面积为4π m2.
课堂练习
课下思考
1.如图,一根5m长的绳子、一端拴在粒子上,另一端栓着一只羊(羊只能在草地上活动),请画出羊的活动区域.
2.设AB=3cm,画图说明∶到点A的距离小子2cm,且到点B的距离大于2cm的所有点组成的图形.
解:如图,以A,B为圆心,2cm为半径画圆且相交。阴影部分即为符合题意的图形(除去圆周上的部分)
1.从运动和集合的观点理解圆的定义.
2.点与圆的位置关系.
3.能根据圆基本元素的特征,解决一些简单的圆问题.
§3.1 圆
北师版九年级下册 圆
1.知道圆的有关定义及表示方法;
2.掌握点和圆的位置关系;
3.会根据要求画出图形.
如图3-1,一些学生正在做投圈游戏、他们的投圈标都是图中的花瓶。如果他们呈"一"字排开,这样的队形对每个人都公平吗 你认为他们应当排成什么样的队形才公平
图3-1
解:不公平.因为圆上任意一点到圆心的距离是相等的,因而排成圆形才能对每个人公平.
若想游戏公平,应排成圆形.
情景导入
如果现在有一条3米长的绳子, 你准备怎么办
小贴士
如何画圆?
1、固定一点;
2、然后选取一定长;
3、绕定点旋转一圈即可.
动态:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的集合.(点的集合)
O
A
A
A
A
A
A
A
A
A
O
·
A
B
C
D
E
r
r
r
r
r
圆的两种定义
新知讲解
定义 平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点称为圆心,定长称为半径.
以点O为圆心的圆记作:
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.
①圆心确定圆的位置;②半径确定圆的大小.两者缺一不可.
⊙O,读作:“圆O”.
新知讲解
Add Text
点击此处添加标题
集合思想
圆的集合定义应用
(2014年河南省)如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,
把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,
DE的长为 .
点题:本题旨在提醒大家:“圆的集合定义”为我们日后解决许多思考困难的问题提供了一个有利的工具。
除圆心、半径以外,还有:
如图3-2,连接圆上任意两点的线段叫做弦(chord),
如 AB;经过圆心的弦叫做直径(dianneter),如CD.
我们知道,圆上任意两点间的部分叫做圆弧
圆的任意一条直经的两个端点分圆成两条弧,每一条弧都叫做半圆
(semicircle ).
能够重合的两个圆叫做等圆(equal circles ).在同图3-2
圆或等圆中,能够互相重合的弧叫做等弧(equal arcs).
新知讲解
圆的基本元素
图3-2
跟踪练习
1、如图,AB是⊙O的直径,C点在⊙O上,那么,哪一段弧是优弧,哪一段弧是劣弧?
2 判断下列说法是否正确
(1)直径是弦.( );(2)弦是直径.( )
(3)半圆是弧.( );(4)弧是半圆.( )
(5)长度相等的两段弧是等弧.( )
(6)等弧的长度相等.( )
(7)两个劣弧之和等于半圆.( )
(8)半径相等的两个半圆是等弧.( )
√
×
√
×
×
√
√
×
点与圆的位置关系
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么
若点A在⊙O内
若点A在⊙O上
若点A在⊙O外
OA<r, OB=r, OC>r.
反过来也成立,即
结论:点的位置可以确定该点到圆心的距离与半径的关系,
反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
新知讲解
设 AB=3 cm,画图说明满足下列要求的图形∶
(1)到点A和点B的距离都等于2cm 的所有点组成的图形;
(2)到点A和点B的距离都小于2cm的所有点组成的图形、
2.小明和小华正在练习投铅球,樊球场地分为五个区域∶4m以内,4~5m,5~6m,6~7m,7m以外.小明投了5.2m,小华投了6.7m,他们投的球分别落在哪个区域内
跟踪练习
解:如图,点C、D即是符合(1)要求的图形;
图中所涂阴影部分即是符合(2)要求的图形.
解:小明投在了5~6m的区域;小华投在了6~7m的区域.
1.下列说法正确的是( )
A.半圆是弧,弧也是半圆
B.过圆上任意一点只能作一条弦,且这条弦是直径
C.弦是直径
D.直径是圆中最长的弦
D
课堂练习
2.下列条件中,能画唯一圆的是( )
A.以已知点O为圆心
B.以点O为圆心,2 cm长为半径
C.以1 cm长为半径
D.经过已知点A,且半径为2 cm
B
课堂练习
3.(2020·安阳林州期末)已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上
C.点P在圆外 D.不能确定
A
课堂练习
4.已知⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
A
课堂练习
5.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=3=r,∴点B在⊙C上.
课堂练习
6.下列命题,其中正确的有( )
①两个端点能够重合的弧是等弧;②面积相等的两个圆是等圆;③弦是圆上任意两点之间的部分;④同圆或等圆中,劣弧比优弧短.
A.1个 B.2个 C.3个 D.4个
B
课堂练习
7.(2020·烟台)量角器测角度时摆放的位置如图所示,在△AOB中,
射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70°
C.80° D.85°
C
课堂练习
C
8.(2019·聊城)如图,BC是半圆O的直径,D,E是BC上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35° B.38°
C.40° D.42°
︵
点题:解决本题的关键是“牢记同圆的半径处处相等”,从而结合等腰三角形的知识解题
课堂练习
9.如图,小虎牵着小狗上街,小虎的手臂与绳共2.5 m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
解:小狗在地面上环绕的圆的半径为r=2(m),
S=πr2=4π(m2),
故小狗在平整的地面上活动的最大区域是以小虎为圆心,2 m长为半径的圆,其面积为4π m2.
课堂练习
课下思考
1.如图,一根5m长的绳子、一端拴在粒子上,另一端栓着一只羊(羊只能在草地上活动),请画出羊的活动区域.
2.设AB=3cm,画图说明∶到点A的距离小子2cm,且到点B的距离大于2cm的所有点组成的图形.
解:如图,以A,B为圆心,2cm为半径画圆且相交。阴影部分即为符合题意的图形(除去圆周上的部分)
1.从运动和集合的观点理解圆的定义.
2.点与圆的位置关系.
3.能根据圆基本元素的特征,解决一些简单的圆问题.
