2021—2022学年北师大版数学九年级下册1.2. 30°、45°、60°角的三角函数值 课件(共19张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册1.2. 30°、45°、60°角的三角函数值 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 14:40:34 | ||
图片预览



文档简介
(共19张PPT)
1.2. 30°、45°、60°角的三角函数值
第一章 直角三角形的边角关系
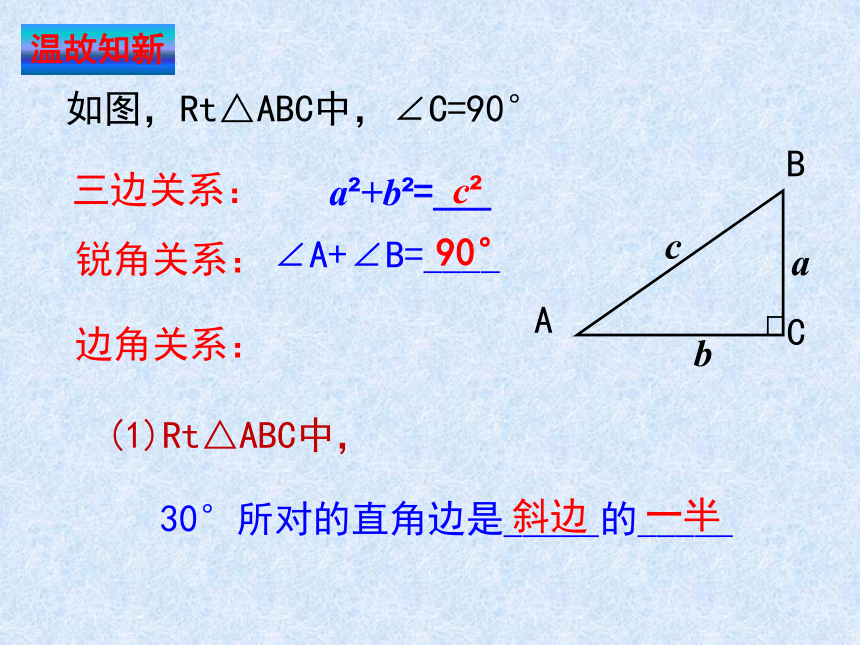
温故知新
三边关系:
A
B
C
如图,Rt△ABC中,∠C=90°
a
b
c
a +b =___
锐角关系:
∠A+∠B=____
90°
边角关系:
(1)Rt△ABC中,
30°所对的直角边是_____的_____
斜边
一半
c
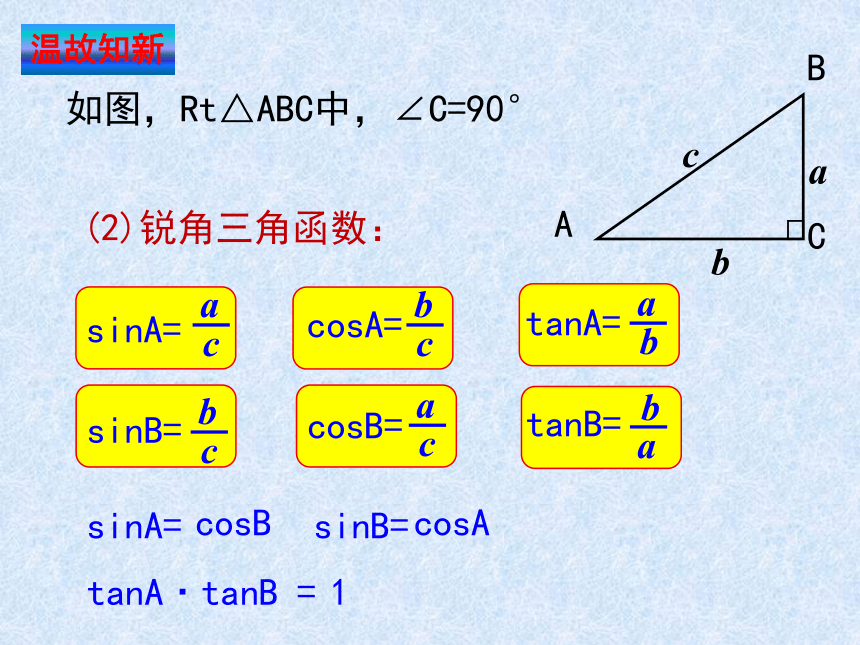
温故知新
A
B
C
sinA=
a
c
cosA=
b
c
tanA=
a
b
如图,Rt△ABC中,∠C=90°
a
b
c
(2)锐角三角函数:
sinB=
a
c
cosB=
b
c
tanB=
a
b
sinA=
sinB=
tanA·tanB =
cosB
cosA
1
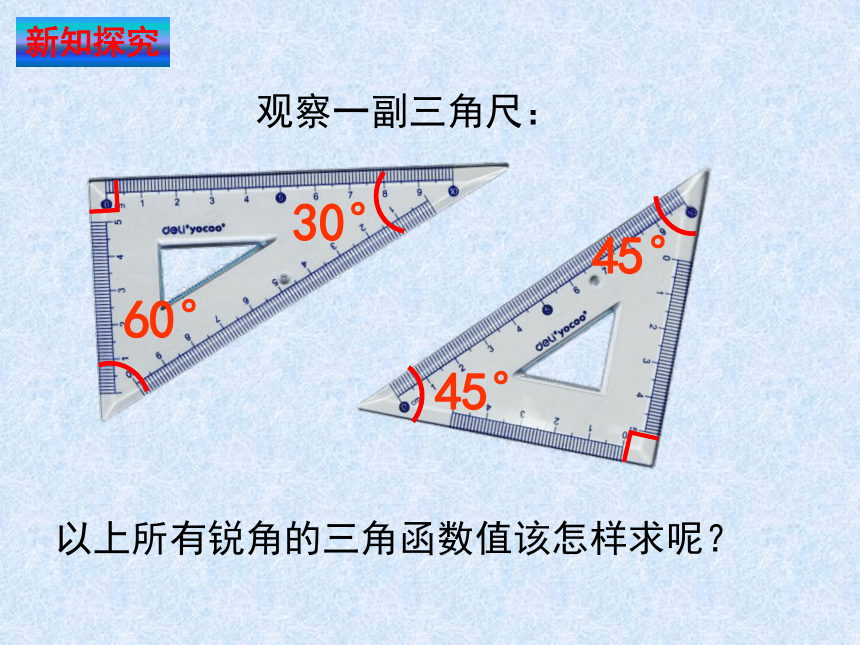
新知探究
观察一副三角尺:
∟
∟
30°
60°
45°
45°
以上所有锐角的三角函数值该怎样求呢?
情境引入
如图,Rt△ABC中,∠C=90°,∠A=30°。
A
B
C
∠B=
设BC=a,
则AB=
60°
2a ,
AC=
a
30°
a
2a
a
sin30°
cos30°
tan30°
60°
a
2a
1
2
=
=
a
2a
2
=
=
a
a
3
=
=
sin60°
cos60°
tan60°
a
2a
2
=
=
a
2a
1
2
=
=
a
a
=
情境引入
Ⅰ、如图,Rt△ABC中,∠C=90°,∠A=45°。
A
B
C
∠B=
设BC=a,
AB=
45°
a ,
AC=
a
45°
a
a
sin45°
cos45°
tan45°
=1
a
a
a
2
=
=
a
a
=
a
a
2
=
=
新知探究
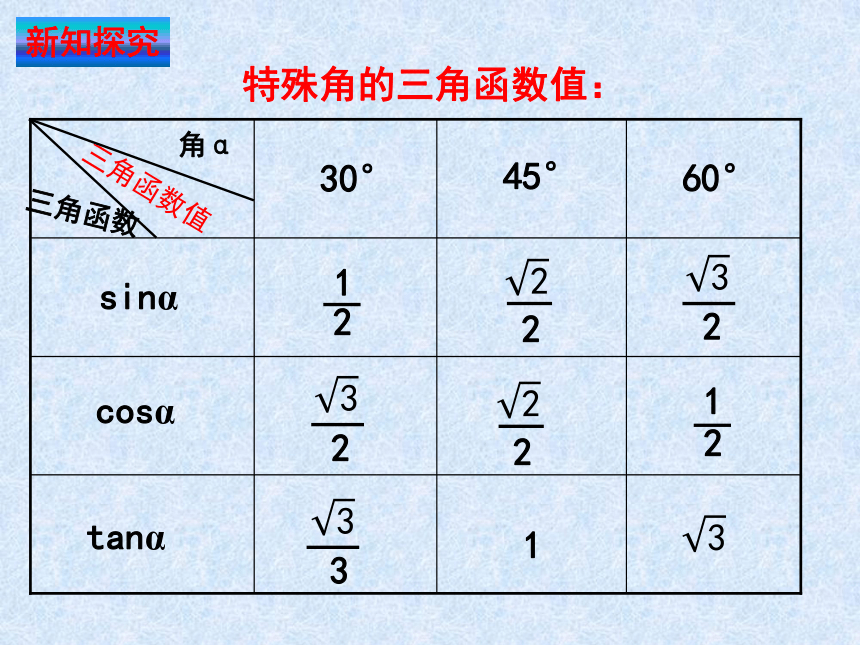
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
新知探究
例1、计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°。
解:
(1)sin30°+cos45°
(2)sin260°+cos260°-tan45°
=
1
2
2
+
=
1+
2
=
2
2
+
2
1
2
-1
=
3
4
+
1
4
-1
=0
例2、一个小孩子荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,视角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m)。
何时摆至最低处
C
O
B
A
D
例题精讲
何时摆至最高处
高度之差=
OA-OC
┐
30°
2.5m
答:最高位置与最低位置的高度差约为0.34m。
C
O
B
A
D
0A=OD=2.5
∵cos∠COD=
OC
OD
∴OC=
=2.5×
2
≈2.165
∴AC=2.5-2.165
≈0.34
例题精讲
解:
Rt△OCD中
根据题意,
∠COD=
1
2
×60°
=30°
OD×cos30°
练一练
D
1.
练一练
2
2.(中考滨州)有下列运算:
sin30°= , =2, π =π,2 =-4,
其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
0
-2
D
练一练
3. tan(α+20°)=1,锐角α的度数应是( )
A.40° B.30°
C.20° D.10°
D
练一练
4.若某三角形三个内角度数之比为1:2:3,那么这个三角形最小角的正切值为( )
A. B. C. D.
2
3
2
3
C
练一练
5.
B
练一练
6.计算:
(1)cos60°-sin45°
(2)tan60°-cos30°
练一练
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
课堂小结
作业
P10
1,2,3,
1.2. 30°、45°、60°角的三角函数值
第一章 直角三角形的边角关系
温故知新
三边关系:
A
B
C
如图,Rt△ABC中,∠C=90°
a
b
c
a +b =___
锐角关系:
∠A+∠B=____
90°
边角关系:
(1)Rt△ABC中,
30°所对的直角边是_____的_____
斜边
一半
c
温故知新
A
B
C
sinA=
a
c
cosA=
b
c
tanA=
a
b
如图,Rt△ABC中,∠C=90°
a
b
c
(2)锐角三角函数:
sinB=
a
c
cosB=
b
c
tanB=
a
b
sinA=
sinB=
tanA·tanB =
cosB
cosA
1
新知探究
观察一副三角尺:
∟
∟
30°
60°
45°
45°
以上所有锐角的三角函数值该怎样求呢?
情境引入
如图,Rt△ABC中,∠C=90°,∠A=30°。
A
B
C
∠B=
设BC=a,
则AB=
60°
2a ,
AC=
a
30°
a
2a
a
sin30°
cos30°
tan30°
60°
a
2a
1
2
=
=
a
2a
2
=
=
a
a
3
=
=
sin60°
cos60°
tan60°
a
2a
2
=
=
a
2a
1
2
=
=
a
a
=
情境引入
Ⅰ、如图,Rt△ABC中,∠C=90°,∠A=45°。
A
B
C
∠B=
设BC=a,
AB=
45°
a ,
AC=
a
45°
a
a
sin45°
cos45°
tan45°
=1
a
a
a
2
=
=
a
a
=
a
a
2
=
=
新知探究
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
新知探究
例1、计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°。
解:
(1)sin30°+cos45°
(2)sin260°+cos260°-tan45°
=
1
2
2
+
=
1+
2
=
2
2
+
2
1
2
-1
=
3
4
+
1
4
-1
=0
例2、一个小孩子荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,视角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m)。
何时摆至最低处
C
O
B
A
D
例题精讲
何时摆至最高处
高度之差=
OA-OC
┐
30°
2.5m
答:最高位置与最低位置的高度差约为0.34m。
C
O
B
A
D
0A=OD=2.5
∵cos∠COD=
OC
OD
∴OC=
=2.5×
2
≈2.165
∴AC=2.5-2.165
≈0.34
例题精讲
解:
Rt△OCD中
根据题意,
∠COD=
1
2
×60°
=30°
OD×cos30°
练一练
D
1.
练一练
2
2.(中考滨州)有下列运算:
sin30°= , =2, π =π,2 =-4,
其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
0
-2
D
练一练
3. tan(α+20°)=1,锐角α的度数应是( )
A.40° B.30°
C.20° D.10°
D
练一练
4.若某三角形三个内角度数之比为1:2:3,那么这个三角形最小角的正切值为( )
A. B. C. D.
2
3
2
3
C
练一练
5.
B
练一练
6.计算:
(1)cos60°-sin45°
(2)tan60°-cos30°
练一练
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
课堂小结
作业
P10
1,2,3,
