2021--2022学年北师大版九年级数学下册 1.5三角函数的应用 课件(共19张PPT)
文档属性
| 名称 | 2021--2022学年北师大版九年级数学下册 1.5三角函数的应用 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 14:44:14 | ||
图片预览






文档简介
(共19张PPT)
北师大版数学九年级(下)
5.三角函数的应用
第一章 直角三角形的边角关系
教学目标
重点难点
1.利用三角函数解决与方向角、仰角、俯角、坡度及坡角相关的问题.(重点)
2.通过做辅助线构造直角三角形,再利用三角函数解决实际问题.(难点)
答一答
教学过程
温故知新
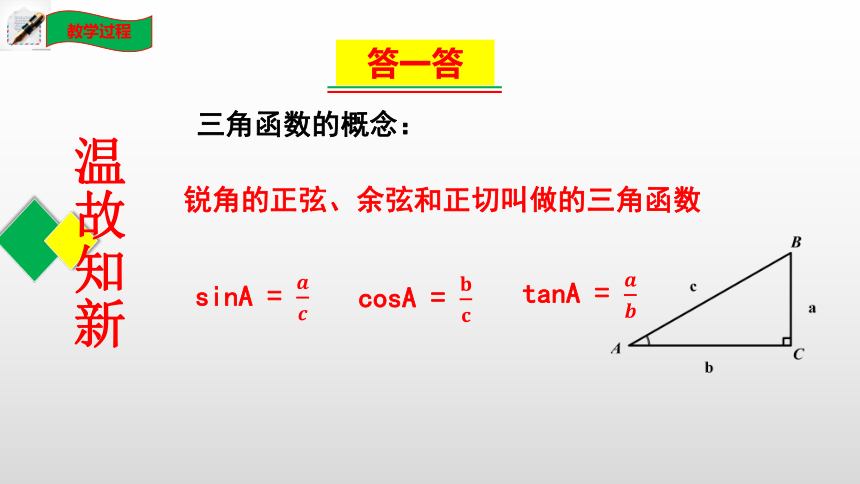
三角函数的概念:
锐角的正弦、余弦和正切叫做的三角函数
sinA =
cosA =
tanA =
议一议
教学过程
新课引入
海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
上面的问题需要用到我们刚学的三角函数知识才能解决.
记一记
教学过程
新知新授
首先需要弄清什么是方向角:
方向角一般是指目标与参照物所在的直线和南北方向所在的直线所夹的锐角.
注意:(1)方向角常写成“北偏东(西)多少度”“南偏东(西)多少度”的形式,而一般不写成“东偏南(北)多少度”“西偏南(北)多少度”的形式.
(2)观测点不同,同一目标所得的方向角不同.
为了解决上面的问题,我们首先需要根据条件画出几何图形,把实际问题转化为数学问题,建立相应的数学模型.
做一做
教学过程
新知新授
根据所画的图形,过A作AD⊥BC于D.
D
作好辅助线后,我们将“货轮继续向东航行途中是否有触礁的危险”的实际问题转化为求线段AD的长,再比较AD的长是否大于10km的一个数学问题了.
做一做
教学过程
新知新授
D
问题解答:
解:设AD=x,根据题意,∠DAB=55°,∠CAD=25°
在Rt△ABD中,tan∠BAD=,
∴BD=AD tan∠BAD=1.43x.
在Rt△ACD中,tan∠CAD=,
∴CD=AD tan∠CAD=0.47x.
∵BC=BD-CD,∴1.43x-0.47x=20.解得 x≈20.8
∵20.8>10,∴货轮继续向东航行途中不会有触礁的危险.
记一记
教学过程
方法总结
应用三角函数解决实际问题的一边步骤:
4.根据题中数量关系或图中线段关系列出方程,求解作答.
1.将实际问题抽象为数学问题(画出平面图形,将原问题转化为解直角三角形的问题);
2.根据题目的要求设出相应的未知数;
3.根据问题中的条件,适当选用锐角三角函数(尽量避免除法运算,尽量使用原始数据);
做一做
教学过程
新知新授
实际生活中除了有方向角问题,还会遇到仰角、俯角和坡度问题.
例1.隧道上方有一块宣传牌CD.在点A测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B、C、D在同一条直线上),AB=10m,隧道高6.5m(即BC=6.5m),求标语牌CD的长.(结果保留小数点后一位,参考数据:sin42°≈0.67,cos42°≈0. 74,tan42°≈0.90,≈1.73.)
做一做
教学过程
新知新授
解:过A作AE⊥BD于E.
E
在Rt△ABE中,∵∠BAE=30°,AB=10,∴BE=AB=5.
∵cos∠BAE=,∴AE=AB cos∠BAE=10×cos30°= 5
∵BC=BE+CE,∴CE=BC-BE=6.5-5=1.5
做一做
教学过程
新知新授
在Rt△DAE中,∠DAE=42°,AE=5
∵tan∠DAE=,∴DE=AE tan∠DAE=5×tan42°≈7.79
∵DE=CE+CD,∴CD=DE-CE=7.80-1.5≈6.3
∴广告牌的高度约为6.3米.
E
例2.某商场准备改善原有楼梯的安全性能,把倾斜角由40°减至35°,已知原楼梯长为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m)
做一做
教学过程
新知新授
解:如图,设梯子原长为AB,加长后的梯子长为AC,梯子高度为AD.
在Rt△ABD中,AB=4,∠ABD=40°.
AD=ABsin∠ABD=4×sin40°≈2.56(米).
BD=AB cos∠ABD=4×cos40°≈3.08(米).
做一做
教学过程
新知新授
在Rt△ACD中,AD=2.56,∠ACD=35°.
AC==≈4.46(米).
CD==≈3.66(米).
∵AC-AB=4.46-4=0.46,BC=CD-BD=3.66-3.08=0.58
∵调整后楼梯加长了约0.46米,楼梯多占地面约0.58米.
做一做
教学过程
随堂练习
完成课本第20页“随堂练习”。
记一记
教学过程
课堂小结
方向角一般是指目标与参照物所在的直线和南北方向所在的直线所夹的锐角.
记一记
教学过程
课堂小结
应用三角函数解决实际问题的一边步骤:
4.根据题中数量关系或图中线段关系列出方程,求解作答.
1.将实际问题抽象为数学问题(画出平面图形,将原问题转化为解直角三角形的问题);
2.根据题目的要求设出相应的未知数;
3.根据问题中的条件,适当选用锐角三角函数(尽量避免除法运算,尽量使用原始数据);
分层作业
教学过程
课后巩固
第一层:课本第21页习题1.6第1、2、3题
第二层:课本第21页习题1.6第2、3、4题
教学过程
结束新课
感谢聆听
北师大版数学九年级(下)
5.三角函数的应用
第一章 直角三角形的边角关系
教学目标
重点难点
1.利用三角函数解决与方向角、仰角、俯角、坡度及坡角相关的问题.(重点)
2.通过做辅助线构造直角三角形,再利用三角函数解决实际问题.(难点)
答一答
教学过程
温故知新
三角函数的概念:
锐角的正弦、余弦和正切叫做的三角函数
sinA =
cosA =
tanA =
议一议
教学过程
新课引入
海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
上面的问题需要用到我们刚学的三角函数知识才能解决.
记一记
教学过程
新知新授
首先需要弄清什么是方向角:
方向角一般是指目标与参照物所在的直线和南北方向所在的直线所夹的锐角.
注意:(1)方向角常写成“北偏东(西)多少度”“南偏东(西)多少度”的形式,而一般不写成“东偏南(北)多少度”“西偏南(北)多少度”的形式.
(2)观测点不同,同一目标所得的方向角不同.
为了解决上面的问题,我们首先需要根据条件画出几何图形,把实际问题转化为数学问题,建立相应的数学模型.
做一做
教学过程
新知新授
根据所画的图形,过A作AD⊥BC于D.
D
作好辅助线后,我们将“货轮继续向东航行途中是否有触礁的危险”的实际问题转化为求线段AD的长,再比较AD的长是否大于10km的一个数学问题了.
做一做
教学过程
新知新授
D
问题解答:
解:设AD=x,根据题意,∠DAB=55°,∠CAD=25°
在Rt△ABD中,tan∠BAD=,
∴BD=AD tan∠BAD=1.43x.
在Rt△ACD中,tan∠CAD=,
∴CD=AD tan∠CAD=0.47x.
∵BC=BD-CD,∴1.43x-0.47x=20.解得 x≈20.8
∵20.8>10,∴货轮继续向东航行途中不会有触礁的危险.
记一记
教学过程
方法总结
应用三角函数解决实际问题的一边步骤:
4.根据题中数量关系或图中线段关系列出方程,求解作答.
1.将实际问题抽象为数学问题(画出平面图形,将原问题转化为解直角三角形的问题);
2.根据题目的要求设出相应的未知数;
3.根据问题中的条件,适当选用锐角三角函数(尽量避免除法运算,尽量使用原始数据);
做一做
教学过程
新知新授
实际生活中除了有方向角问题,还会遇到仰角、俯角和坡度问题.
例1.隧道上方有一块宣传牌CD.在点A测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B、C、D在同一条直线上),AB=10m,隧道高6.5m(即BC=6.5m),求标语牌CD的长.(结果保留小数点后一位,参考数据:sin42°≈0.67,cos42°≈0. 74,tan42°≈0.90,≈1.73.)
做一做
教学过程
新知新授
解:过A作AE⊥BD于E.
E
在Rt△ABE中,∵∠BAE=30°,AB=10,∴BE=AB=5.
∵cos∠BAE=,∴AE=AB cos∠BAE=10×cos30°= 5
∵BC=BE+CE,∴CE=BC-BE=6.5-5=1.5
做一做
教学过程
新知新授
在Rt△DAE中,∠DAE=42°,AE=5
∵tan∠DAE=,∴DE=AE tan∠DAE=5×tan42°≈7.79
∵DE=CE+CD,∴CD=DE-CE=7.80-1.5≈6.3
∴广告牌的高度约为6.3米.
E
例2.某商场准备改善原有楼梯的安全性能,把倾斜角由40°减至35°,已知原楼梯长为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m)
做一做
教学过程
新知新授
解:如图,设梯子原长为AB,加长后的梯子长为AC,梯子高度为AD.
在Rt△ABD中,AB=4,∠ABD=40°.
AD=ABsin∠ABD=4×sin40°≈2.56(米).
BD=AB cos∠ABD=4×cos40°≈3.08(米).
做一做
教学过程
新知新授
在Rt△ACD中,AD=2.56,∠ACD=35°.
AC==≈4.46(米).
CD==≈3.66(米).
∵AC-AB=4.46-4=0.46,BC=CD-BD=3.66-3.08=0.58
∵调整后楼梯加长了约0.46米,楼梯多占地面约0.58米.
做一做
教学过程
随堂练习
完成课本第20页“随堂练习”。
记一记
教学过程
课堂小结
方向角一般是指目标与参照物所在的直线和南北方向所在的直线所夹的锐角.
记一记
教学过程
课堂小结
应用三角函数解决实际问题的一边步骤:
4.根据题中数量关系或图中线段关系列出方程,求解作答.
1.将实际问题抽象为数学问题(画出平面图形,将原问题转化为解直角三角形的问题);
2.根据题目的要求设出相应的未知数;
3.根据问题中的条件,适当选用锐角三角函数(尽量避免除法运算,尽量使用原始数据);
分层作业
教学过程
课后巩固
第一层:课本第21页习题1.6第1、2、3题
第二层:课本第21页习题1.6第2、3、4题
教学过程
结束新课
感谢聆听
