数轴

花园中心校南校区七年级数学讲学稿（四）
班级： 姓名：
内容：数轴2第四课时 课型：新授
一、学习目标与重点和难点：
1．使学生进一步理解有理数与数轴上的点的对应关系。
2．会借用数轴直观的进行有理数的大小比较，体会数形结合的数学思想。
重点：会用数轴比较有理数的大小。
难点：如何比较负有理数的大小。
教学过程：
二、自学指导
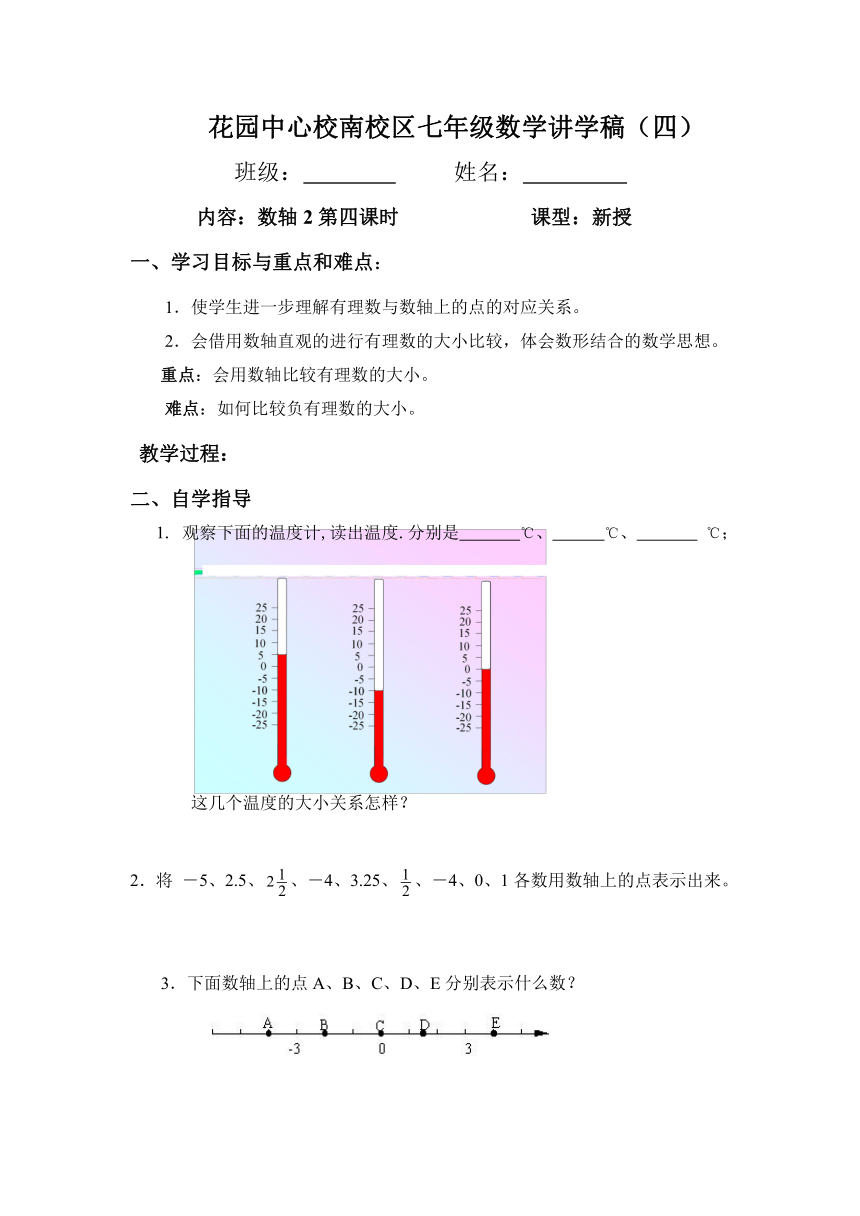
1. 观察下面的温度计,读出温度.分别是 ℃、 ℃、 ℃；
这几个温度的大小关系怎样？
2．将 ―5、2.5、、―4、3.25、、―4、0、1各数用数轴上的点表示出来。
3．下面数轴上的点A、B、C、D、E分别表示什么数？
4．用“＜”或“＞”填空：（简单复习小学有关比较正整数、正分数、正小数的大小的知识）
25 17；0.9 0.85；3.7 2.9； ； 。
三、合作交流 自主学习：
发现、总结：
观察温度计的刻度，发现上边的温度总比下边的 。类似地，在数轴上表示的两个数，右边的数总比左边的数大。
进一步观察数轴，发现所有的负数都在“0”的 ，所有的正数都在“0”的 ，这说明什么？
归纳：正数都大于 ；负数都小于 ；正数大于一切 。
例1：比较―3，0，2的大小。
分析一：先在数轴上分别找到表示―3、0、2的点，由“右边的数总比左边的数大”得到―3＜0＜2；
分析二：直接由“正数都大于0；负数都小于0；正数大于一切负数”的规律得出―3＜0＜2。
例2：把下列各组数用“＜”号连接起来．
(1) ―10， 2，―14； (2) ―100，0，0.01； (3) ，―4.75，3.75。
解：(1) ； (2) ；(3) 。
说明：按题意用“＜”号连接，解题中不能用“＞”号连接，否则与题意不符，更不能把“＜”与“＞”混用，如第（1）小题不能写成“―10＜2＞―14”或者写成“2＞―14＜―10”的形式。
例3：利用数轴比较下列各数的大小： ―1.3，0.3，―3，―5 .
解：
四、课堂小结：
比较有理数大小法则是：在数轴上表示的两个数，右边的数总比左边的数 。
根据法则先在同一个数轴上表示出同一组数的位置，然后用“＜”号连接，这种方法比较直观，但画图表示数较麻烦。
另一种方法是：利用数轴上数的位置得出比较大小规律，即正数都大于 ，负数都小于 ，正数大于一切 .
五、当堂训练:
1．在数轴上表示的两个数中， 的数总比 的数大。
2．在数轴上，表示－5的数在原点的 侧，它到原点的距离是 个单位长度。
3．在数轴上，表示+2的点在原点的 侧，距原点 个单位；表示－7的点在原点的 侧，距原点 个单位；两点之间的距离为 个单位长度。
4．在数轴上，把表示3的点沿着数轴向负方向移动5个单位，则与此位置相对应的数是 。
5．与原点距离为2.5个单位长度的点有 个，它们表示的有理数是 。
6．到原点的距离不大于3的整数有 个，它们是： 。
7．下列说法正确的是（ ）
A.没有最大的正数，却有最大的负数 B.数轴上离原点越远，表示数越大
C.0大于一切非负数 D.在原点左边离原点越远，数就越小
8．下列结论正确的有（ ）个：
① 规定了原点，正方向和单位长度的直线叫数轴 ② 最小的整数是0 ③ 正数，负数和零统称有理数 ④ 数轴上的点都表示有理数
A.0 B.1 C.2 D.3
9．在数轴上，A点和B点所表示的数分别为－2和1，若使A点表示的数是B点表示的数的3倍，应把A点 （ ）
A.向左移动5个单位 B.向右移动5个单位
C.向右移动4个单位 D.向左移动1个单位或向右移动5个单位
10.（2011四川重庆）在－6，0，3，8 这四个数中，最小的数是( )
A．－6 B．0 C．3 D．8
[能力拓展]
数轴上与原点距离是5的点有＿＿＿个，表示的数是＿＿＿。
已知x是整数，并且-3＜x＜4，那么在数轴上表示x的所有可能的数值有＿＿＿＿＿＿。
在数轴上，点A、B分别表示-5和2，则线段AB的长度是＿＿＿。
从数轴上表示-1的点出发，向左移动两个单位长度到点B，则点B表示的数是＿＿＿，再向右移动两个单位长度到达点C,则点C表示的数是＿＿＿。
数轴上的点A表示-3，将点A先向右移动7个单位长度，再向左移动5个单位长度，那么终点到原点的距离是＿＿＿个单位长度。
体验中招
1、（2009年，太原）在数轴上表示-2的点离开原点的距离等于（ ）
A、2 B、-2 C、±2 D、4
2、（2009年，广州）有理数a、b在数轴上的位置如图所示，则a、b的大小关系是（ ）
A、a＜b B、a＞b C、a=b D、无法确定
0
a
b