【北师大版】数学九年级上册 4.3 相似多边形 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 4.3 相似多边形 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
课前预习
预习新知
各角分别相等,各边成比例的两个多
边形叫做相似多边形
2.相似多边形对应边的比叫做相似比
3.相似多边形的性质:对应角相等,对应边
成比例
4.相似多边形的判定:①对应角相等,
②对应边成比例,判定两个多边形相似
这两个条件缺一不可
堂训练
巩固基础
知识点1相似多边形的识别
下列图形中不一定是相似图形的是
A.两个等边三角形
B.两个等腰直角三角形
C.两个菱形
D.两个正方形
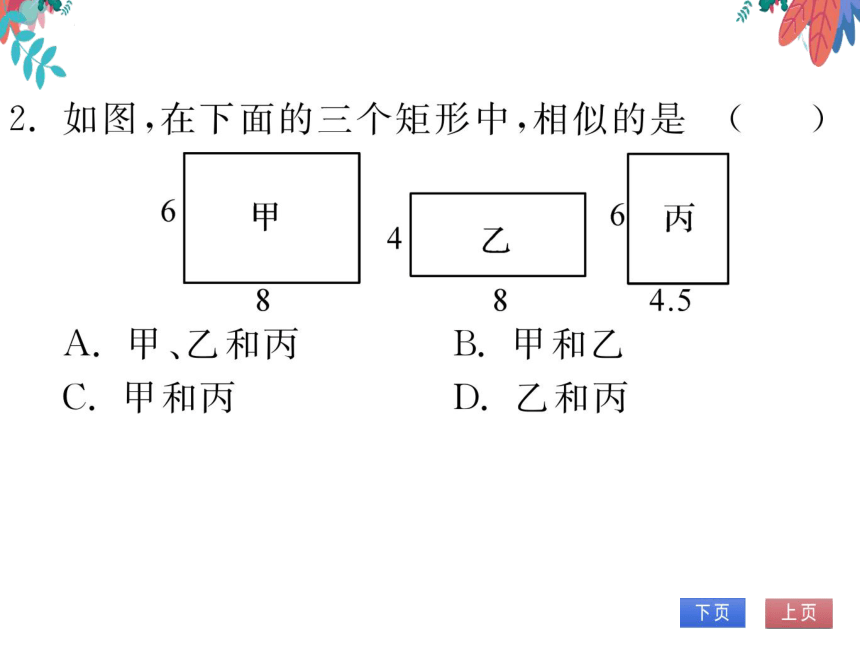
2.如图,在下面的三个矩形中,相似的是((
甲
6丙
乙
4.5
A.甲、乙和丙
B.甲和乙
C.甲和丙
D.乙和丙
边数相同的多边形相似应具备的条件是
A.各角对应相等
B.各边对应成比例
C.各角对应相等,各边对应相等
D.各角对应相等,各边对应成比例
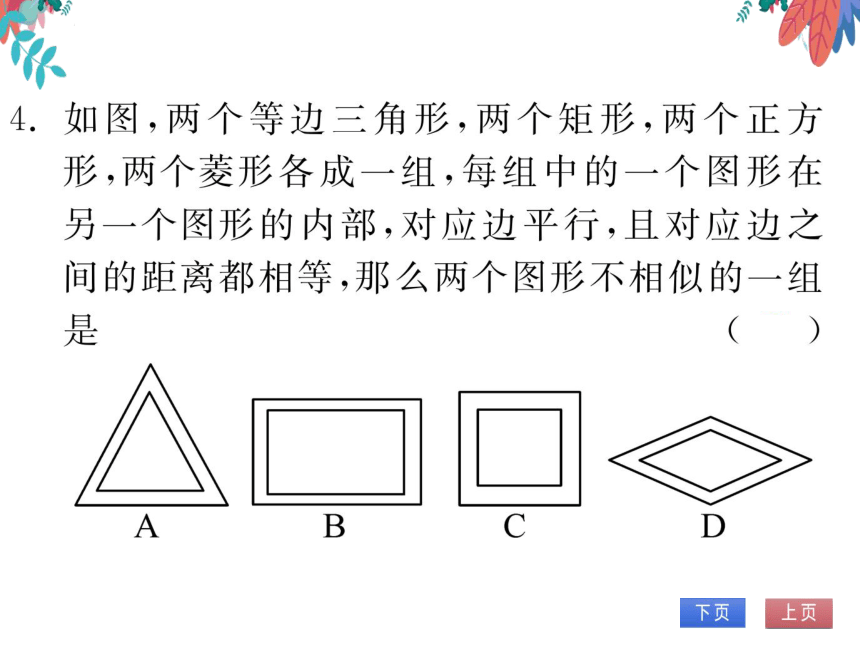
4.如图,两个等边三角形,两个矩形,两个正方
形,两个菱形各成一组,每组中的一个图形在
另一个图形的内部,对应边平行,且对应边之
间的距离都相等,那么两个图形不相似的一组
B
知识点2相似多边形的性质
5.一个多边形的边长分别为2,3,4,5,6,另一个
多边形和它相似且最长边为24,则这个多边
形的最短边长为
A.6
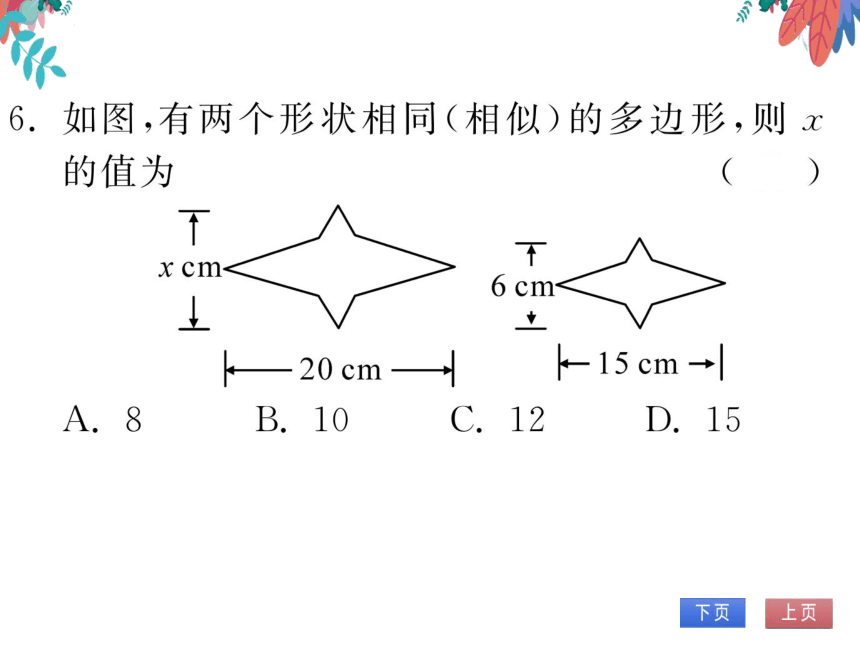
如图,有两个形状相同(相似)的多边形,则x
的值为
(A)
cm
6 cm<
k-20 cm
k15cm
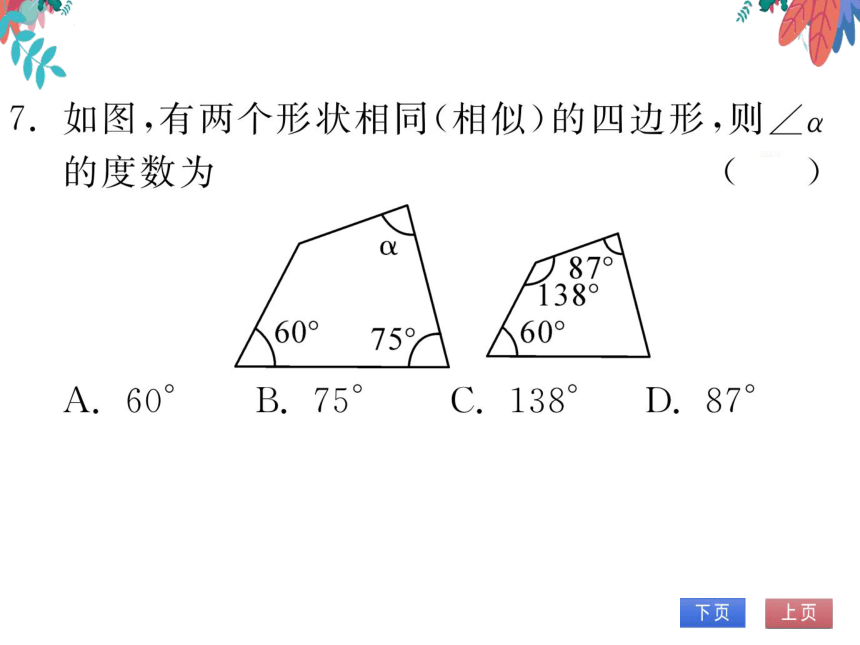
图,有两个形状相同(相似)的四边形,则∠a
的度数为
87
38
60°
75
60°
60
D,87°
8.如图,已知五边形 ABCDE和五边形 ABC DE
相似,AB=BC=CD=4cm,DE=3cm,AE
2cm,AB=2cm,∠C=85°
(1)求∠BCD的度数;
(2)求CD和DE的长
解:(1)∵五边形 ABCDE∽五
边形 ABCDE′
∠BCD
C=85
(2)由相似性,得aB=CD
AB
E
解:∵矩形ABCD与矩形
DEFC相似,
DEEF,而2
AB BC
DE
DE
AE=AD
课后作业
全面提升
1.如图,在长为8cm,宽为4cm的矩形中,截去
个矩形,使得留下的矩形(图中阴影部分)与
原矩形相似,则留下矩形的面积是
B. 4c
8 c
2.要做甲、乙两个形状相同(相似)的三角形框
架,已知三角形框架甲的三边长分别为:
50cm,60cm,80cm,三角形框架乙的一边长
为20cm,那么符合条件的三角形框架乙共有
A.1种B.2种C.3种D.4种
3.(黄岛)复印纸的型号有A。,A1,A2,A3,A4等,
它们之间存在着这样一种关系:将其中某一型
课前预习
预习新知
各角分别相等,各边成比例的两个多
边形叫做相似多边形
2.相似多边形对应边的比叫做相似比
3.相似多边形的性质:对应角相等,对应边
成比例
4.相似多边形的判定:①对应角相等,
②对应边成比例,判定两个多边形相似
这两个条件缺一不可
堂训练
巩固基础
知识点1相似多边形的识别
下列图形中不一定是相似图形的是
A.两个等边三角形
B.两个等腰直角三角形
C.两个菱形
D.两个正方形
2.如图,在下面的三个矩形中,相似的是((
甲
6丙
乙
4.5
A.甲、乙和丙
B.甲和乙
C.甲和丙
D.乙和丙
边数相同的多边形相似应具备的条件是
A.各角对应相等
B.各边对应成比例
C.各角对应相等,各边对应相等
D.各角对应相等,各边对应成比例
4.如图,两个等边三角形,两个矩形,两个正方
形,两个菱形各成一组,每组中的一个图形在
另一个图形的内部,对应边平行,且对应边之
间的距离都相等,那么两个图形不相似的一组
B
知识点2相似多边形的性质
5.一个多边形的边长分别为2,3,4,5,6,另一个
多边形和它相似且最长边为24,则这个多边
形的最短边长为
A.6
如图,有两个形状相同(相似)的多边形,则x
的值为
(A)
cm
6 cm<
k-20 cm
k15cm
图,有两个形状相同(相似)的四边形,则∠a
的度数为
87
38
60°
75
60°
60
D,87°
8.如图,已知五边形 ABCDE和五边形 ABC DE
相似,AB=BC=CD=4cm,DE=3cm,AE
2cm,AB=2cm,∠C=85°
(1)求∠BCD的度数;
(2)求CD和DE的长
解:(1)∵五边形 ABCDE∽五
边形 ABCDE′
∠BCD
C=85
(2)由相似性,得aB=CD
AB
E
解:∵矩形ABCD与矩形
DEFC相似,
DEEF,而2
AB BC
DE
DE
AE=AD
课后作业
全面提升
1.如图,在长为8cm,宽为4cm的矩形中,截去
个矩形,使得留下的矩形(图中阴影部分)与
原矩形相似,则留下矩形的面积是
B. 4c
8 c
2.要做甲、乙两个形状相同(相似)的三角形框
架,已知三角形框架甲的三边长分别为:
50cm,60cm,80cm,三角形框架乙的一边长
为20cm,那么符合条件的三角形框架乙共有
A.1种B.2种C.3种D.4种
3.(黄岛)复印纸的型号有A。,A1,A2,A3,A4等,
它们之间存在着这样一种关系:将其中某一型
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
