【北师大版】数学九年级上册 4.4 第2课时 两边成比例且夹角相等的两个三角形相似 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 4.4 第2课时 两边成比例且夹角相等的两个三角形相似 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:13:37 | ||
图片预览



文档简介
(共23张PPT)
课前预习
预习新知
1.两边成比例且夹角相等的两个三角
形相似
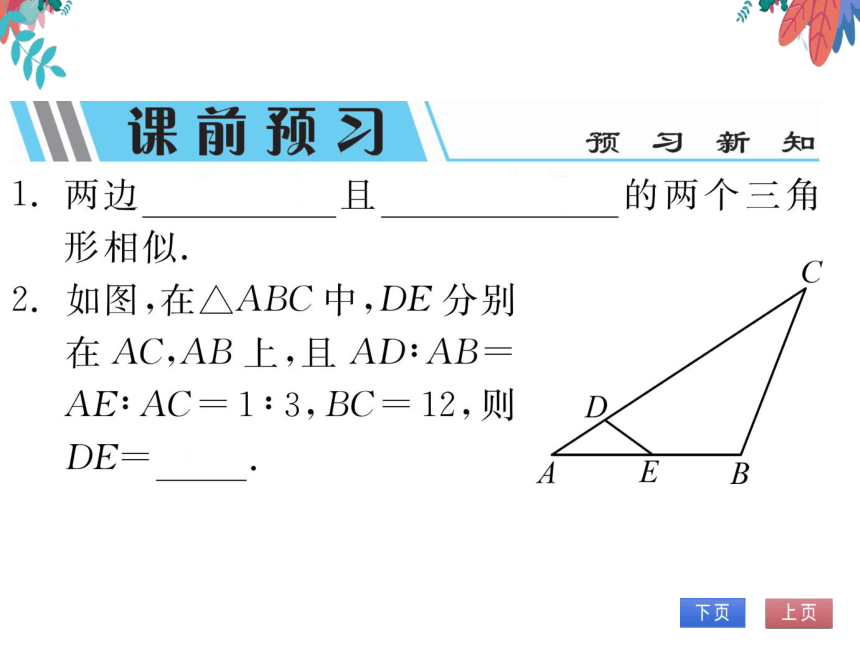
2.如图,在△ABC中,DE分别
在AC,AB上,且AD:AB
AE:AC=1:3,BC=12,则
DE
4
E
B
堂训练
巩固基础
知识点两边成比例且夹角相等的两个三角
形相似
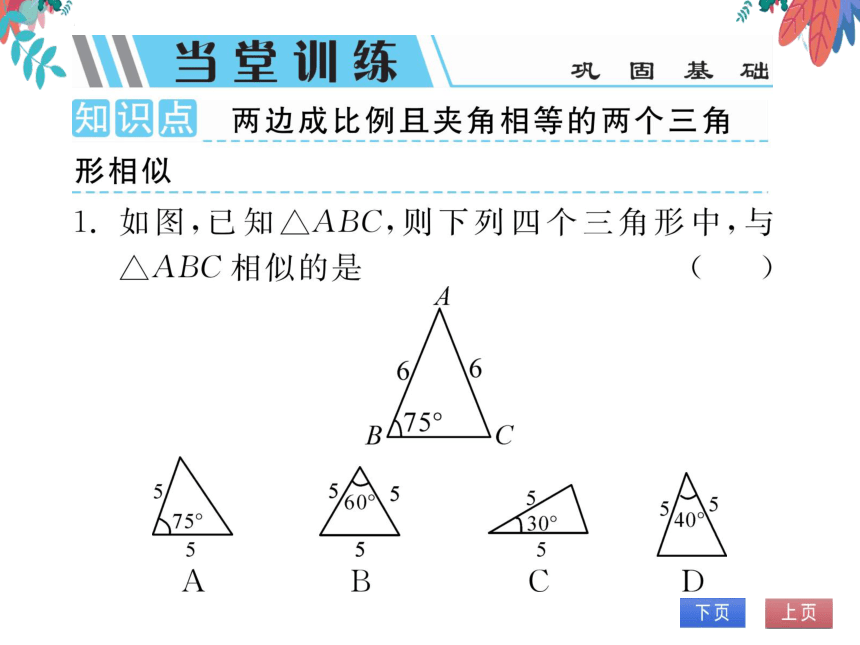
如图,知△ABC,则下列四个三角形中,与
△ABC相似的是
6
B475°
C
605
75°
△30°
40°
5
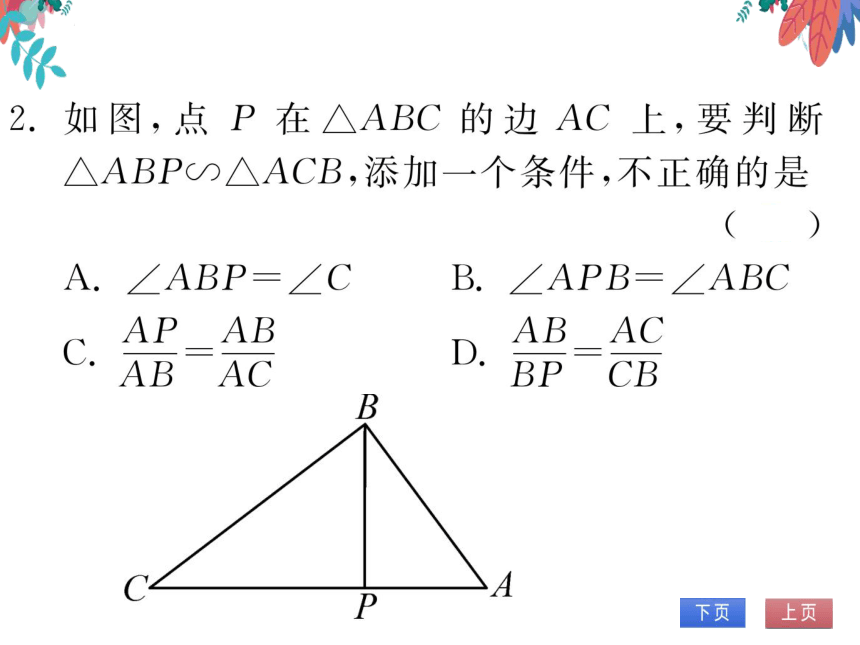
2.如图,点P在△ABC的边AC上,要判断
△ABP∽△ACB,添加一个条件,不正确的是
A.∠ABP=∠C
B.∠APB=∠ABC
ap aB
Ab AC
ab A
BP CB
B
P
第2题图
D
C
B
第3题图
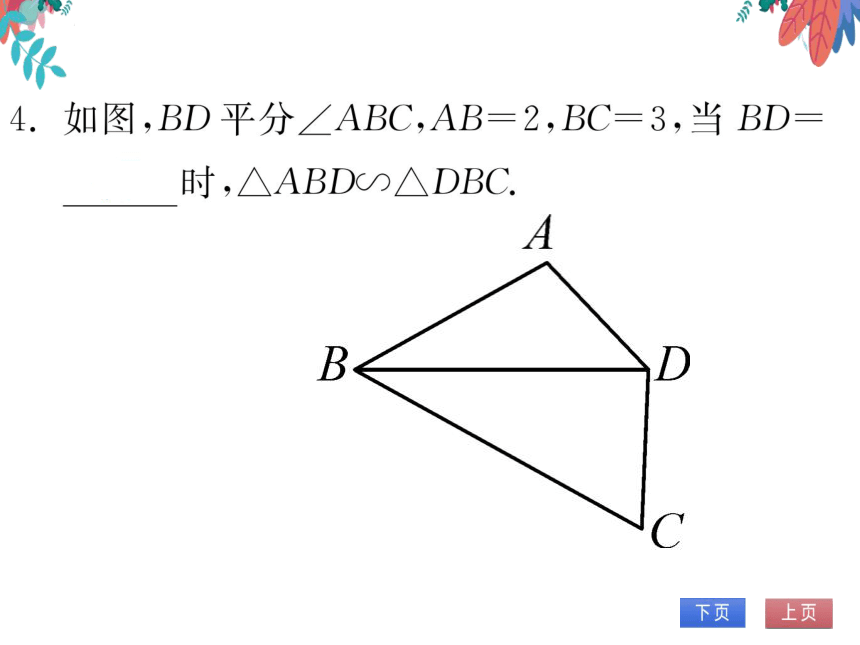
B
D
C
(第4题图)
B
eCr
第5题图
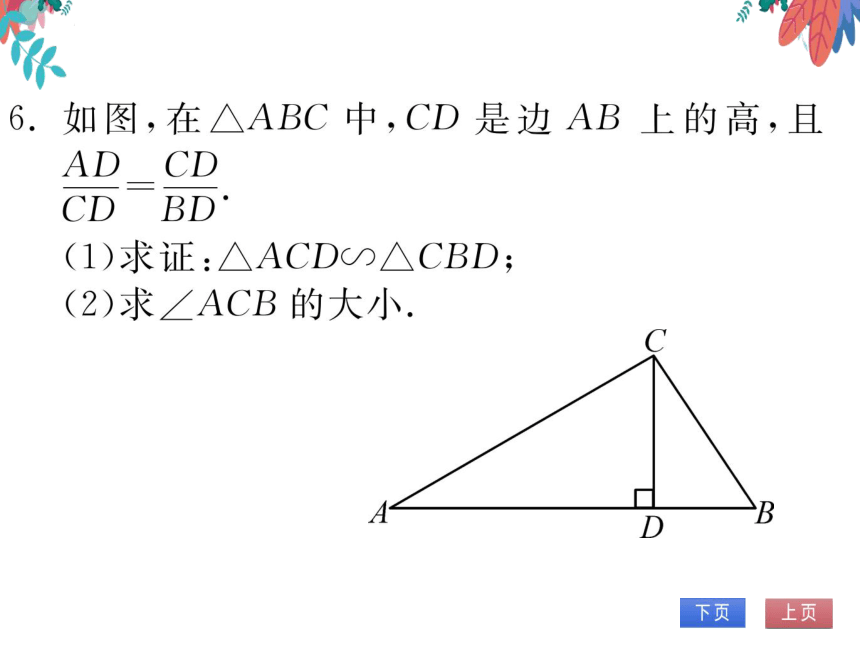
如图,在△ABC中,CD是边AB上的高,且
AD cD
CD bD
(1)求证:△ACDO△CBD;
(2)求∠ACB的大小
A
D
1)证明:CD是边
AB上的高,
ADC=∠CDB=90
又:ADCD
CD BD
ACDc△CBD
(2)解:∵△ACB∽△CBD
A=∠BCD.
在△ACD中,∠ADC=90
∠A+∠ACD=90
BCD+∠ACD=90°,即∠ACB=90°
B
C
证明:在正方形ABCD中,
AD
Q是CD的中点
又∵BP=3PC.BC
PC=4,
DQ
又∵BC=2DQ,
8.如图,点C,D在线段AB上,且△PCD是等边
角形
(1)当AC,CD,DB满足怎样的关系时
ACP∽△PDB
(2)当△PDB∽△ACP时,试求∠APB的
度数
D
B
解:(1)满足CD
AC·DB时即可
理由为:△PCD为
等边三角形
PCD=∠PDC=60,∴∠ACP=∠PDB
又∵CD=AC·DB.CDDB
AC CD
PD BD
CD=CP=PD,··ACPC
△ACP△PDB
2)∠APB=120
课后作业
全面提升
1.如图,已知∠1=∠2,那么添加下列一个条件
后,仍无法判定△ABC∽△ADE的是(D
A.∠C=∠E
B.∠B=∠ADE
AB AC
D AB
bc
AD DE
B
D
(第1题图)
2.如图,四边形ABCD的对角线AC,BD相交于
点O,且将这个四边形分成①②③④四个三角
形.若OA:OC=OB:OD,则下列结论中
定正确的是
B
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
②2
B
3
第2题图
课前预习
预习新知
1.两边成比例且夹角相等的两个三角
形相似
2.如图,在△ABC中,DE分别
在AC,AB上,且AD:AB
AE:AC=1:3,BC=12,则
DE
4
E
B
堂训练
巩固基础
知识点两边成比例且夹角相等的两个三角
形相似
如图,知△ABC,则下列四个三角形中,与
△ABC相似的是
6
B475°
C
605
75°
△30°
40°
5
2.如图,点P在△ABC的边AC上,要判断
△ABP∽△ACB,添加一个条件,不正确的是
A.∠ABP=∠C
B.∠APB=∠ABC
ap aB
Ab AC
ab A
BP CB
B
P
第2题图
D
C
B
第3题图
B
D
C
(第4题图)
B
eCr
第5题图
如图,在△ABC中,CD是边AB上的高,且
AD cD
CD bD
(1)求证:△ACDO△CBD;
(2)求∠ACB的大小
A
D
1)证明:CD是边
AB上的高,
ADC=∠CDB=90
又:ADCD
CD BD
ACDc△CBD
(2)解:∵△ACB∽△CBD
A=∠BCD.
在△ACD中,∠ADC=90
∠A+∠ACD=90
BCD+∠ACD=90°,即∠ACB=90°
B
C
证明:在正方形ABCD中,
AD
Q是CD的中点
又∵BP=3PC.BC
PC=4,
DQ
又∵BC=2DQ,
8.如图,点C,D在线段AB上,且△PCD是等边
角形
(1)当AC,CD,DB满足怎样的关系时
ACP∽△PDB
(2)当△PDB∽△ACP时,试求∠APB的
度数
D
B
解:(1)满足CD
AC·DB时即可
理由为:△PCD为
等边三角形
PCD=∠PDC=60,∴∠ACP=∠PDB
又∵CD=AC·DB.CDDB
AC CD
PD BD
CD=CP=PD,··ACPC
△ACP△PDB
2)∠APB=120
课后作业
全面提升
1.如图,已知∠1=∠2,那么添加下列一个条件
后,仍无法判定△ABC∽△ADE的是(D
A.∠C=∠E
B.∠B=∠ADE
AB AC
D AB
bc
AD DE
B
D
(第1题图)
2.如图,四边形ABCD的对角线AC,BD相交于
点O,且将这个四边形分成①②③④四个三角
形.若OA:OC=OB:OD,则下列结论中
定正确的是
B
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
②2
B
3
第2题图
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
