【北师大版】数学九年级上册 4.5 相似三角形判定定理的证明 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 4.5 相似三角形判定定理的证明 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:13:37 | ||
图片预览




文档简介
(共25张PPT)
课前预习
领弓新知
1.两角分别相等的两个三角形相似
2.两边成比例且夹角相等的两个三角
形相似
边成比例的两个三角形相似
堂训练
巩固基础
知识点1两角分别相等的两个三角形相似
1.如图,点P是□ABCD边AB上的一点,射线
CP交DA的延长线于点E,则图中相似的三
角形有
E
B
A.1对
C.3对
D.4对
2.如图,四边形ABCD是菱形,对角线AC,BD
相交于点O,过点D作DH⊥AB于点H,交
AO于点G,连接OH.
(1)求证:AG·GO=HG·GD
(2)若∠ABC=120°,AB=6,求OG的长
B
1)证明:∵四边形ABCD是
菱形
AC⊥BD
又∵DH⊥AB于点H
DHA=∠DOG=90
又∵∠AGH=∠DGO,
△AGH∽△DGO
AG HG
DG OG
AG·GO=HG·GD
2)解:∵四边形ABCD是菱形,
ABC=120°
DAB=60.AB=AD-6
△ABD是等边三角形
AC⊥DB,∴OD=O=1
BD=3
又∵DH⊥AB,
ODG=30.OG
知识点2两边成比例且夹角相等的两个三角
形相似
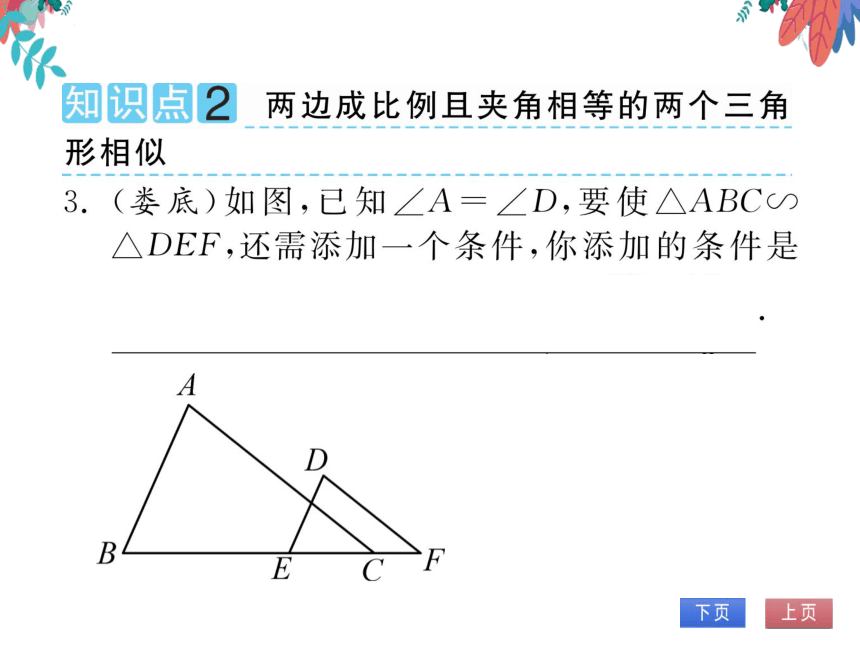
娄底)如图,已知∠A=∠D,要使△ABC∽
△DEF,还需添加一个条件,你添加的条件是
AB AC
B=∠DEF或∠ACB=∠F或
DEDE
D
B
E
(第3题图)
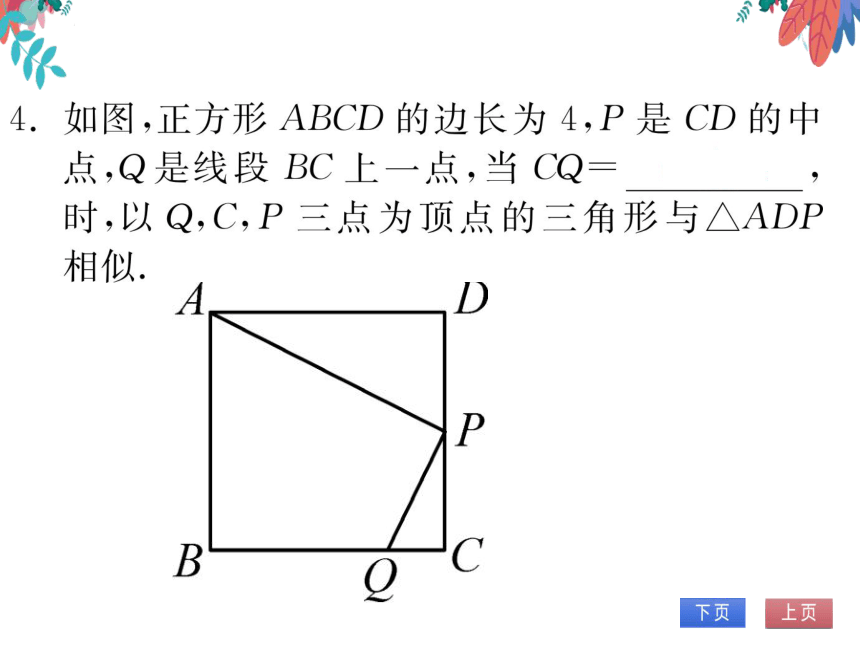
4.如图,正方形ABCD的边长为4,P是CD的
点,Q是线段BC上一点,当QQ=4或1,
时,以Q,C,P三点为顶点的三角形与△ADP
相似
P
B
C
(第4题图)
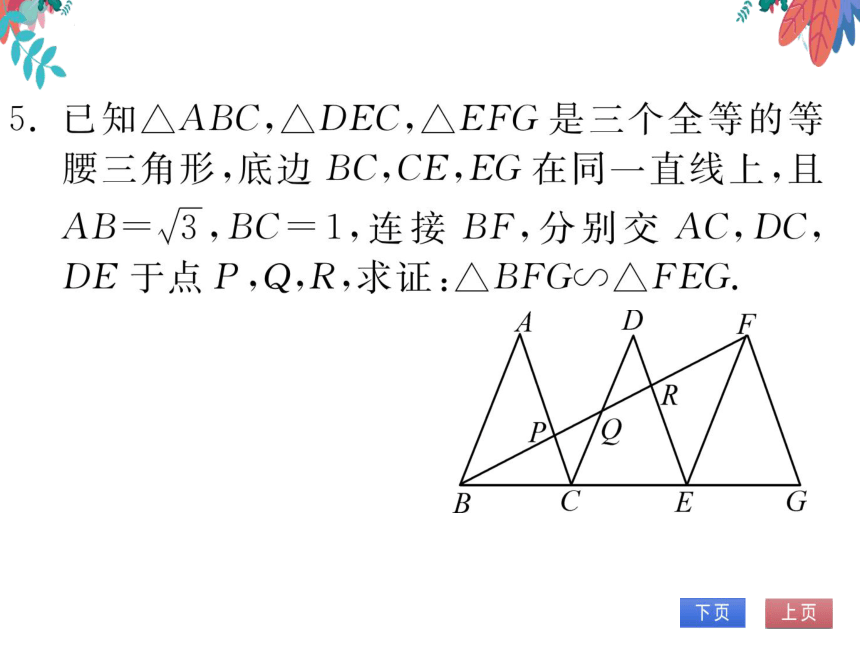
已知△ABC,△DEC,△EFG是三个全等的等
腰三角形,底边BC,CE,EG在同一直线上,且
AB=√3,BC=1,连接BF,分别交AC,DC
DE于点P,Q,R,求证:△BFG∽△FEG
R
B
E
△ABC
△DCE≌△FEG,
BC=CE-EG=I
AB-FG=3
bG=3
BG
FO
FG
又
EG 1
BG FG
FG EG
又
G,∴.△BFG△FEG
知识点3三边成比例的两个三角形相似
6.下列条件中能使△ABC与△DEF相似的是
A. AB=6,BC=6,AC=9
DE=4,EF=4.DF=6
B. AB=4bc=6.ac-8
DE=5,EF=10,DF=15
AB=1,BC=√2,AC=2;
DE=√6,EF=√3,DF
D. AB=l, BC
,AC=3;
DE=√15,EF=23,DF=6
课前预习
领弓新知
1.两角分别相等的两个三角形相似
2.两边成比例且夹角相等的两个三角
形相似
边成比例的两个三角形相似
堂训练
巩固基础
知识点1两角分别相等的两个三角形相似
1.如图,点P是□ABCD边AB上的一点,射线
CP交DA的延长线于点E,则图中相似的三
角形有
E
B
A.1对
C.3对
D.4对
2.如图,四边形ABCD是菱形,对角线AC,BD
相交于点O,过点D作DH⊥AB于点H,交
AO于点G,连接OH.
(1)求证:AG·GO=HG·GD
(2)若∠ABC=120°,AB=6,求OG的长
B
1)证明:∵四边形ABCD是
菱形
AC⊥BD
又∵DH⊥AB于点H
DHA=∠DOG=90
又∵∠AGH=∠DGO,
△AGH∽△DGO
AG HG
DG OG
AG·GO=HG·GD
2)解:∵四边形ABCD是菱形,
ABC=120°
DAB=60.AB=AD-6
△ABD是等边三角形
AC⊥DB,∴OD=O=1
BD=3
又∵DH⊥AB,
ODG=30.OG
知识点2两边成比例且夹角相等的两个三角
形相似
娄底)如图,已知∠A=∠D,要使△ABC∽
△DEF,还需添加一个条件,你添加的条件是
AB AC
B=∠DEF或∠ACB=∠F或
DEDE
D
B
E
(第3题图)
4.如图,正方形ABCD的边长为4,P是CD的
点,Q是线段BC上一点,当QQ=4或1,
时,以Q,C,P三点为顶点的三角形与△ADP
相似
P
B
C
(第4题图)
已知△ABC,△DEC,△EFG是三个全等的等
腰三角形,底边BC,CE,EG在同一直线上,且
AB=√3,BC=1,连接BF,分别交AC,DC
DE于点P,Q,R,求证:△BFG∽△FEG
R
B
E
△ABC
△DCE≌△FEG,
BC=CE-EG=I
AB-FG=3
bG=3
BG
FO
FG
又
EG 1
BG FG
FG EG
又
G,∴.△BFG△FEG
知识点3三边成比例的两个三角形相似
6.下列条件中能使△ABC与△DEF相似的是
A. AB=6,BC=6,AC=9
DE=4,EF=4.DF=6
B. AB=4bc=6.ac-8
DE=5,EF=10,DF=15
AB=1,BC=√2,AC=2;
DE=√6,EF=√3,DF
D. AB=l, BC
,AC=3;
DE=√15,EF=23,DF=6
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
