【北师大版】数学九年级上册 4.8 第1课时 位似的概念及其性质 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 4.8 第1课时 位似的概念及其性质 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:13:37 | ||
图片预览






文档简介
(共23张PPT)
课前预习
领习新知
1.如果两个相似多边形任意一组对应顶点P,P′
所在的直线都经过同一点O,且有OP
k·OP(k≠0),那么这样的两个多边形叫做
位似多边形,点O叫做位似中心,
k就是这两个相似多边形的相似比
2.位似多边形的性质:
(1)位似多边形上任意一对对应点,到位似中
心的距离之比等于位似比
(2)位似多边形上对应点和位似中心在同
条直线上
(3)位似多边形上的对应线段平行或在同
条直线上
(4)位似多边形是特殊的相似图形,因此
具备相似图形的一切性质
堂训练
巩固基础
知识点1位似图形的概念
下列说法中,正确的是
A.两个图形如果是位似图形,那么它们一定
全等
B.两个图形如果是位似图形,那么它们不
定相似
两个图形如果是相似图形,那么它们一定
位似
D.两个图形如果是位似图形,那么它们一定
相似
2.用作位似图形的方法可以将一个图形放大或
缩小,位似中心的位置可选在
A.原图形内部
B.原图形外部
C.原图形边上
D.任意位置
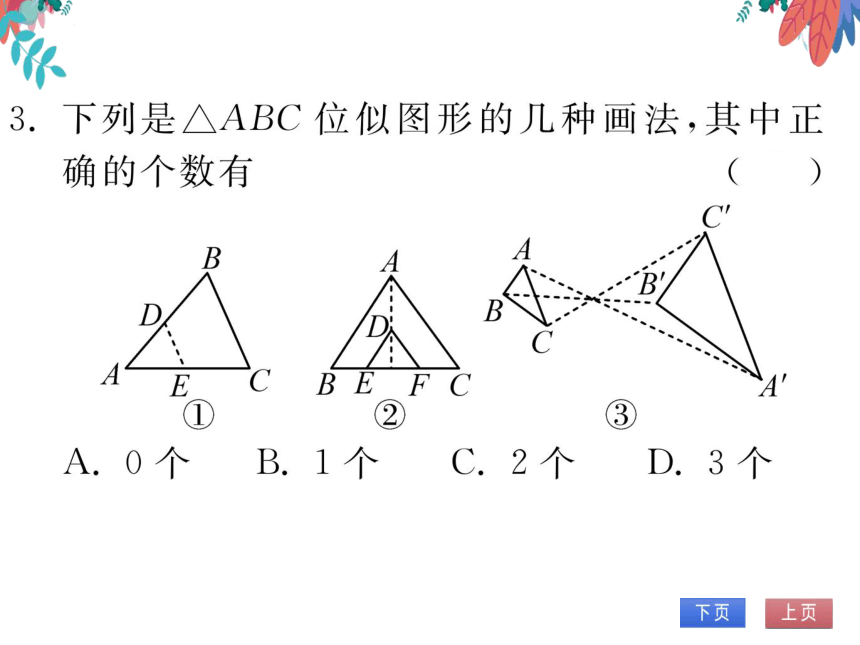
下列是△ABC位似图形的几种画法,其中正
确的个数有
B
B
E CBE FO
3
B
C.2个D.3
知识点2位似图形的性质及画法
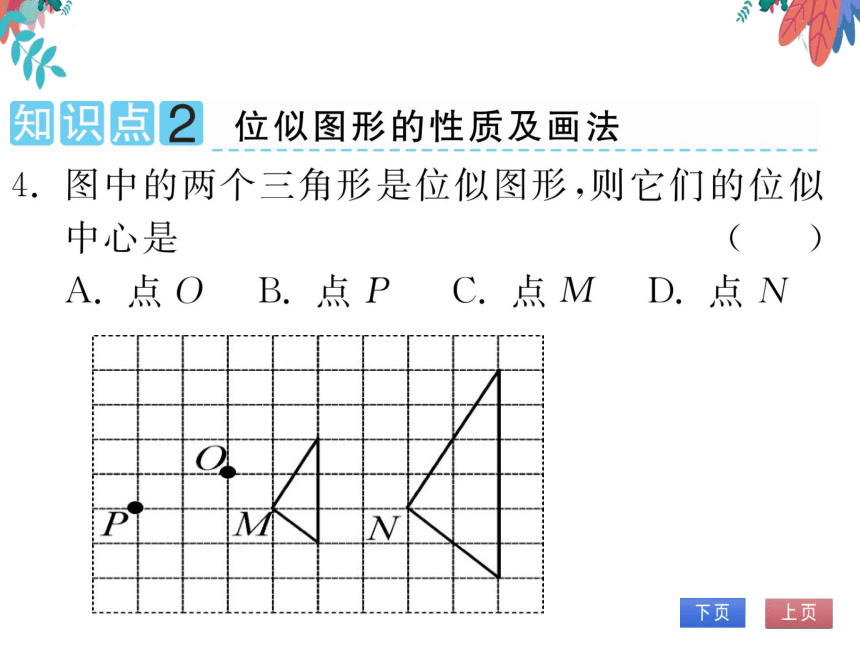
4.图中的两个三角形是位似图形,则它们的位似
中心是
B
A.点OB.点PC.点MD.点N
第4题图
B
B
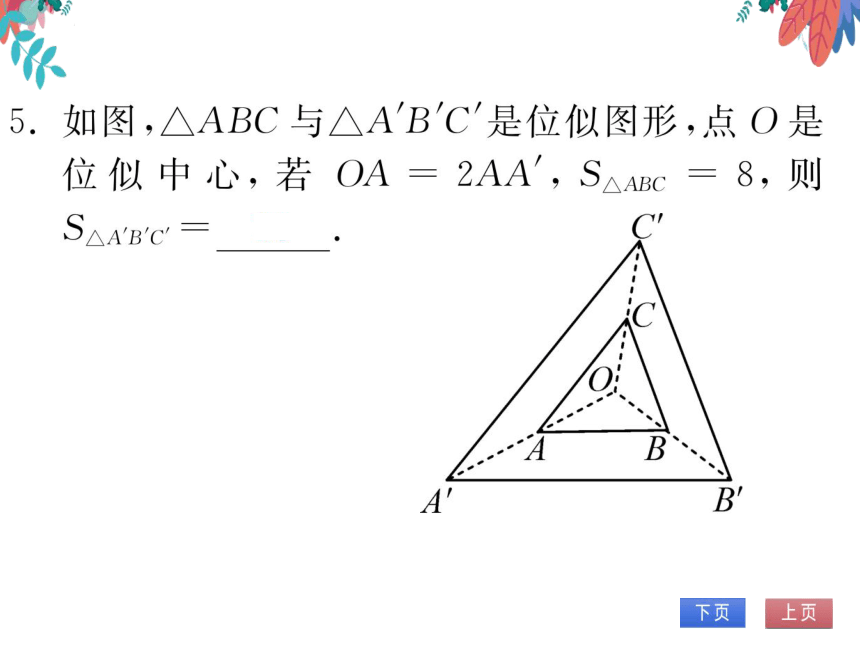
第5题图
按要求进行位似变换(分别画出符合条件的
个位似图形)
(1)如图,将△ABC放大2倍,且位似中心选
在△ABC左侧图中点O处;
解:如图:
(2)如图,将四边形ABCD缩小到原来的
且位似中心选在图形的内部图中点O处
解:如图
7.如图,已知四边形ABCD和四边ABCD是
位似图形,点O为位似中心,OA=AA,求四
边形ABCD与四边形ABCD的周长比和
面积比
O
山==55
3
B
解:∵两个四边形
是位似图形,且
OA=AA′,
OA:OA=1: 2
AB
AB′OA2
,即相似比为
四边形ABCD
AB AB 1
四边形AB'CD
ABA B
四边形ABCD
AB
四边形ABCD
4
课后作业
全面提升
1.如图,下列由位似变换得到的图形中,面积比
是1:9的是
OA=1.204OA=AA′
OA=2AA
OA=6AA
2.如图,不是位似图形的有
D
D米方 B EDo"D
B
A'ARBOAA BB
3
A.1个B.2个C.3个D.4个
3.如图,矩形ABCD中,AB=9,BC=6,若矩形
AEFG与矩形ABCD位似,位似比为,则C
F之间的距离为
A
3B.2√13C.3√13D.12
课前预习
领习新知
1.如果两个相似多边形任意一组对应顶点P,P′
所在的直线都经过同一点O,且有OP
k·OP(k≠0),那么这样的两个多边形叫做
位似多边形,点O叫做位似中心,
k就是这两个相似多边形的相似比
2.位似多边形的性质:
(1)位似多边形上任意一对对应点,到位似中
心的距离之比等于位似比
(2)位似多边形上对应点和位似中心在同
条直线上
(3)位似多边形上的对应线段平行或在同
条直线上
(4)位似多边形是特殊的相似图形,因此
具备相似图形的一切性质
堂训练
巩固基础
知识点1位似图形的概念
下列说法中,正确的是
A.两个图形如果是位似图形,那么它们一定
全等
B.两个图形如果是位似图形,那么它们不
定相似
两个图形如果是相似图形,那么它们一定
位似
D.两个图形如果是位似图形,那么它们一定
相似
2.用作位似图形的方法可以将一个图形放大或
缩小,位似中心的位置可选在
A.原图形内部
B.原图形外部
C.原图形边上
D.任意位置
下列是△ABC位似图形的几种画法,其中正
确的个数有
B
B
E CBE FO
3
B
C.2个D.3
知识点2位似图形的性质及画法
4.图中的两个三角形是位似图形,则它们的位似
中心是
B
A.点OB.点PC.点MD.点N
第4题图
B
B
第5题图
按要求进行位似变换(分别画出符合条件的
个位似图形)
(1)如图,将△ABC放大2倍,且位似中心选
在△ABC左侧图中点O处;
解:如图:
(2)如图,将四边形ABCD缩小到原来的
且位似中心选在图形的内部图中点O处
解:如图
7.如图,已知四边形ABCD和四边ABCD是
位似图形,点O为位似中心,OA=AA,求四
边形ABCD与四边形ABCD的周长比和
面积比
O
山==55
3
B
解:∵两个四边形
是位似图形,且
OA=AA′,
OA:OA=1: 2
AB
AB′OA2
,即相似比为
四边形ABCD
AB AB 1
四边形AB'CD
ABA B
四边形ABCD
AB
四边形ABCD
4
课后作业
全面提升
1.如图,下列由位似变换得到的图形中,面积比
是1:9的是
OA=1.204OA=AA′
OA=2AA
OA=6AA
2.如图,不是位似图形的有
D
D米方 B EDo"D
B
A'ARBOAA BB
3
A.1个B.2个C.3个D.4个
3.如图,矩形ABCD中,AB=9,BC=6,若矩形
AEFG与矩形ABCD位似,位似比为,则C
F之间的距离为
A
3B.2√13C.3√13D.12
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
