【北师大版】数学九年级上册 第1章 特殊平行四边形 整合与提高 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 第1章 特殊平行四边形 整合与提高 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:13:37 | ||
图片预览




文档简介
(共21张PPT)
考点专训
考点1菱形
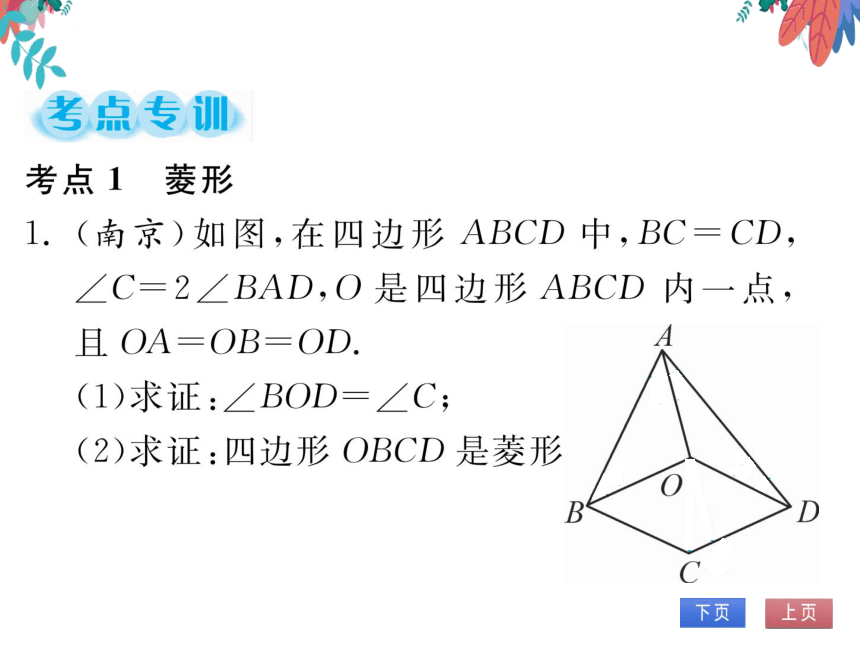
1.(南京)如图,在四边形ABCD中,BC=CD
∠C=2∠BAD,O是四边形ABCD内一点,
且OA=OB=OD
(1)求证:∠BOD=∠C;
(2)求证:四边形OBCD是菱形
B
D
E
证明:(1)延长AO到点E
OA=OB,∴∠3=∠4.
又∠BOE=∠3+∠4
∠BOE=2∠3
同理∠DOE=2∠1
(2)连接O
B=OD. CB=CD.OC=OC
△OBC≌△ODC,∴,∠BOC=∠DOC,
BCO=∠DCO.∴∠BOC
2BCo I
∠BCD
BOC=∠BCO
考点2矩形
(张家界)如图,在矩形ABCD中,点E在BC
上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长
B
证明:(1)在矩形ABCL
中,∵AD∥BC
∠AEB=∠DAF,
又∵DF⊥AE,
∠DFA=90
∠DFA=∠B
又∵.AD=EA,
ADF≌△EAB
DE=AB
2)解:∠ADF+∠FDC=90
∠DAF+∠ADF=90
∠FDC=∠DAF=30
AD=2DF
DF=AB,∴.AD=2AB=8
考点3正方形
3.(遵义)如图,正方形ABCD的对角线交于点
O,点E,F分别在AB,BC上(AEEOF=90°,OE,DA的延长线交于点M
OF,AB的延长线交于点N,连接MN
(1)求证OM=ON;
(2)若正方形ABCD的边长为4,E为OM的
中点,求MN的长
H
证明:(1)∵四边形ABCD
是正方形,
OA=OB,∠DAO=45,
OBA=45°,
∠OAM
OBN
又∵∠EOF=90°,∠AOB=90°
∠AOM=∠BON
△OAM≌△OBN(ASA)
(2)解:过O点作OH⊥AD于点H
正方形ABCD的边长为4,
OHEHA=2
E为OM的中点,∴HM=4
则OM
+42=2
MN=2OM=210
优生特训
1.如图,四边形ABCD中,AB=BC,∠ABC
∠CDA=90°,BE⊥AD于点E,且四边形
ABCD的面积为8,则BE等于
A.2
B.3
B
AE
D
(第1题图)
2.如图,在矩形ABCD中,AB=3cm,AD
4cm,过对角线BD的中点O作BD的垂直平
分线EF,分别交AD,BC于点E,F,则AE的
长为
78
cm
D
B
F
(第2题图)
考点专训
考点1菱形
1.(南京)如图,在四边形ABCD中,BC=CD
∠C=2∠BAD,O是四边形ABCD内一点,
且OA=OB=OD
(1)求证:∠BOD=∠C;
(2)求证:四边形OBCD是菱形
B
D
E
证明:(1)延长AO到点E
OA=OB,∴∠3=∠4.
又∠BOE=∠3+∠4
∠BOE=2∠3
同理∠DOE=2∠1
(2)连接O
B=OD. CB=CD.OC=OC
△OBC≌△ODC,∴,∠BOC=∠DOC,
BCO=∠DCO.∴∠BOC
2
∠BCD
BOC=∠BCO
考点2矩形
(张家界)如图,在矩形ABCD中,点E在BC
上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长
B
证明:(1)在矩形ABCL
中,∵AD∥BC
∠AEB=∠DAF,
又∵DF⊥AE,
∠DFA=90
∠DFA=∠B
又∵.AD=EA,
ADF≌△EAB
DE=AB
2)解:∠ADF+∠FDC=90
∠DAF+∠ADF=90
∠FDC=∠DAF=30
AD=2DF
DF=AB,∴.AD=2AB=8
考点3正方形
3.(遵义)如图,正方形ABCD的对角线交于点
O,点E,F分别在AB,BC上(AE
OF,AB的延长线交于点N,连接MN
(1)求证OM=ON;
(2)若正方形ABCD的边长为4,E为OM的
中点,求MN的长
H
证明:(1)∵四边形ABCD
是正方形,
OA=OB,∠DAO=45,
OBA=45°,
∠OAM
OBN
又∵∠EOF=90°,∠AOB=90°
∠AOM=∠BON
△OAM≌△OBN(ASA)
(2)解:过O点作OH⊥AD于点H
正方形ABCD的边长为4,
OHEHA=2
E为OM的中点,∴HM=4
则OM
+42=2
MN=2OM=210
优生特训
1.如图,四边形ABCD中,AB=BC,∠ABC
∠CDA=90°,BE⊥AD于点E,且四边形
ABCD的面积为8,则BE等于
A.2
B.3
B
AE
D
(第1题图)
2.如图,在矩形ABCD中,AB=3cm,AD
4cm,过对角线BD的中点O作BD的垂直平
分线EF,分别交AD,BC于点E,F,则AE的
长为
78
cm
D
B
F
(第2题图)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
