【北师大版】数学九年级上册 第4章 图形的相似 整合与提高 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 第4章 图形的相似 整合与提高 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览

文档简介
(共25张PPT)
考点专训
考点1相似三角形的判定与性质
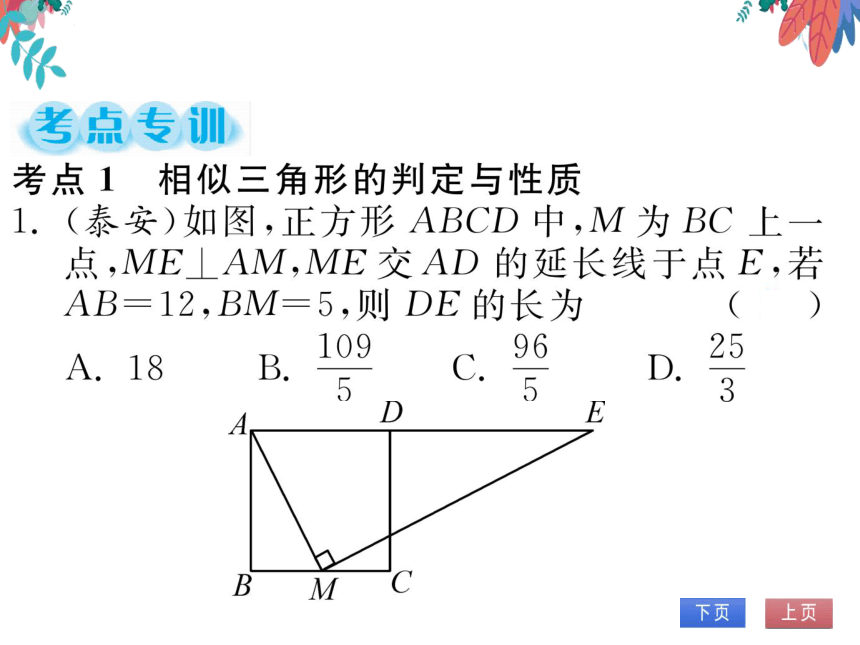
1.(泰安)如图,正方形ABCD中,M为BC上
点,ME⊥AM,ME交AD的延长线于点E,若
AB=12,BM=5,则DE的长为
109
96
25
D
BM
(第1题图)
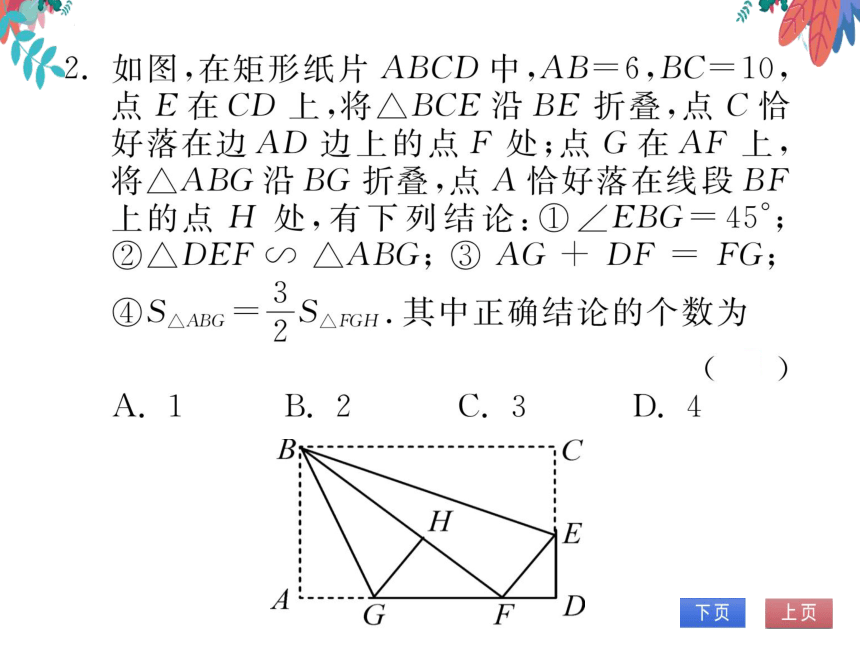
如图,在矩形纸片ABCD中,AB=6,BC=10,
点E在CD上,将△BCE沿BE折叠,点C恰
好落在边AD边上的点F处;点G在AF上
将△ABG沿BG折叠,点A恰好落在线段BF
上的点H处,有下列结论:①∠EBG=45°;
②△DEF0△ABG;③AG+DF=FG
△ABG
S△RH.其中正确结论的个数为
B
H
E
F
第2题图)
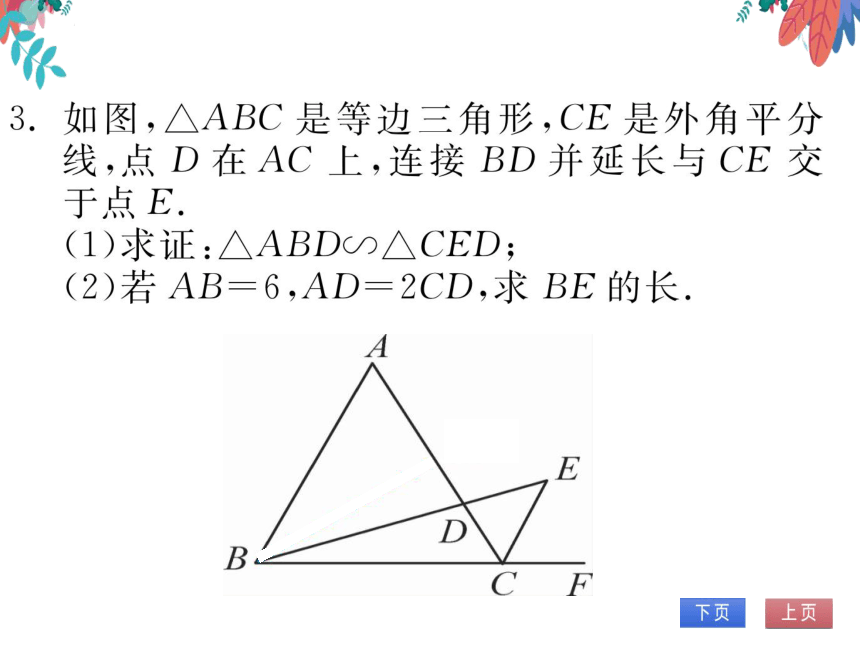
3.如图,△ABC是等边三角形,CE是外角平分
线,点D在AC上,连接BD并延长与CE交
于点E
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长
E
B
(1)证明:△ABC是等边
角形,∴∠A=∠ACB
60°,∴∠ACF=120
CE是外角平分线,
∠ACE
∠ACF
60
ACE.又∵∠ADB=∠CDE,
△ABDC△CED
(2)解:作BM⊥AC于点M,则AM=CM=3,
BM=33
AD=2CD.CD=2.AD=4
MD=1.在Rt△BDM中,BD
BM2+MD2=2√7.由△ABDC△CED,得
ED CD 4027
BD AD
ED2
ED
,∴BE=BD+
Ed=3
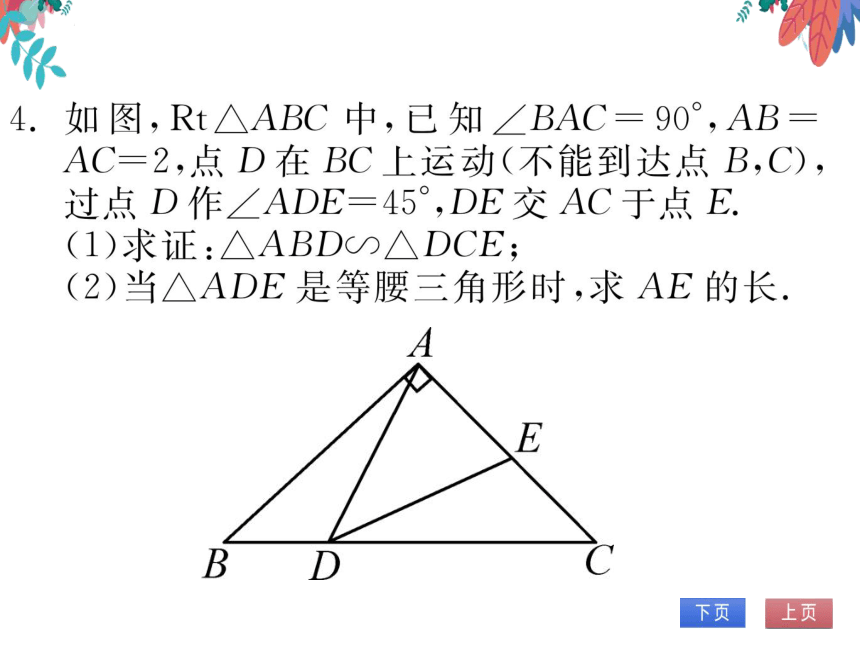
4.如图,Rt△ABC中,已知∠BAC=90°,AB
AC=2,点D在BC上运动(不能到达点B,C)
过点D作∠ADE=45°,DE交AC于点E
1)求证:△ABD△DCE;
(2)当△ADE是等腰三角形时,求AE的长
B D
1)证明:Rt△ABC
BAC=90°,AB=AC
2,∴.∠B=∠C=4
∠ADC
B
BAD,∠ADC
ADE
BAD.又
ADE=45°,∴45°+∠EDC
45+∠BAD.∴∠EDC=∠BAD
△ABD∽△DCE
(2)解:讨论:①若AD=AE时,∠DAE=90
此时D点与点B重合,不合题意
若AD=DE时,△ABD与△DCE的相似
匕为1,此时△ABD≌△DCE,于是AB
AC-2,BC-22,AE-AC-EC-2-BD
2-(2√2-2)=4-22.③若AE=DE,此时
DAE=∠ADE=45°,画草图易知AD
BC,DE⊥AC,且AD=DC.由等腰三角形的
线合一可知AE=CE
AC=1.综上所
述,AE=4-22或1
考点专训
考点1相似三角形的判定与性质
1.(泰安)如图,正方形ABCD中,M为BC上
点,ME⊥AM,ME交AD的延长线于点E,若
AB=12,BM=5,则DE的长为
109
96
25
D
BM
(第1题图)
如图,在矩形纸片ABCD中,AB=6,BC=10,
点E在CD上,将△BCE沿BE折叠,点C恰
好落在边AD边上的点F处;点G在AF上
将△ABG沿BG折叠,点A恰好落在线段BF
上的点H处,有下列结论:①∠EBG=45°;
②△DEF0△ABG;③AG+DF=FG
△ABG
S△RH.其中正确结论的个数为
B
H
E
F
第2题图)
3.如图,△ABC是等边三角形,CE是外角平分
线,点D在AC上,连接BD并延长与CE交
于点E
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长
E
B
(1)证明:△ABC是等边
角形,∴∠A=∠ACB
60°,∴∠ACF=120
CE是外角平分线,
∠ACE
∠ACF
60
ACE.又∵∠ADB=∠CDE,
△ABDC△CED
(2)解:作BM⊥AC于点M,则AM=CM=3,
BM=33
AD=2CD.CD=2.AD=4
MD=1.在Rt△BDM中,BD
BM2+MD2=2√7.由△ABDC△CED,得
ED CD 4027
BD AD
ED2
ED
,∴BE=BD+
Ed=3
4.如图,Rt△ABC中,已知∠BAC=90°,AB
AC=2,点D在BC上运动(不能到达点B,C)
过点D作∠ADE=45°,DE交AC于点E
1)求证:△ABD△DCE;
(2)当△ADE是等腰三角形时,求AE的长
B D
1)证明:Rt△ABC
BAC=90°,AB=AC
2,∴.∠B=∠C=4
∠ADC
B
BAD,∠ADC
ADE
BAD.又
ADE=45°,∴45°+∠EDC
45+∠BAD.∴∠EDC=∠BAD
△ABD∽△DCE
(2)解:讨论:①若AD=AE时,∠DAE=90
此时D点与点B重合,不合题意
若AD=DE时,△ABD与△DCE的相似
匕为1,此时△ABD≌△DCE,于是AB
AC-2,BC-22,AE-AC-EC-2-BD
2-(2√2-2)=4-22.③若AE=DE,此时
DAE=∠ADE=45°,画草图易知AD
BC,DE⊥AC,且AD=DC.由等腰三角形的
线合一可知AE=CE
AC=1.综上所
述,AE=4-22或1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
