【北师大版】数学九年级上册 第4章 专题五 与相似三角形相关的计算及探究问题 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 第4章 专题五 与相似三角形相关的计算及探究问题 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:11:55 | ||
图片预览



文档简介
(共20张PPT)
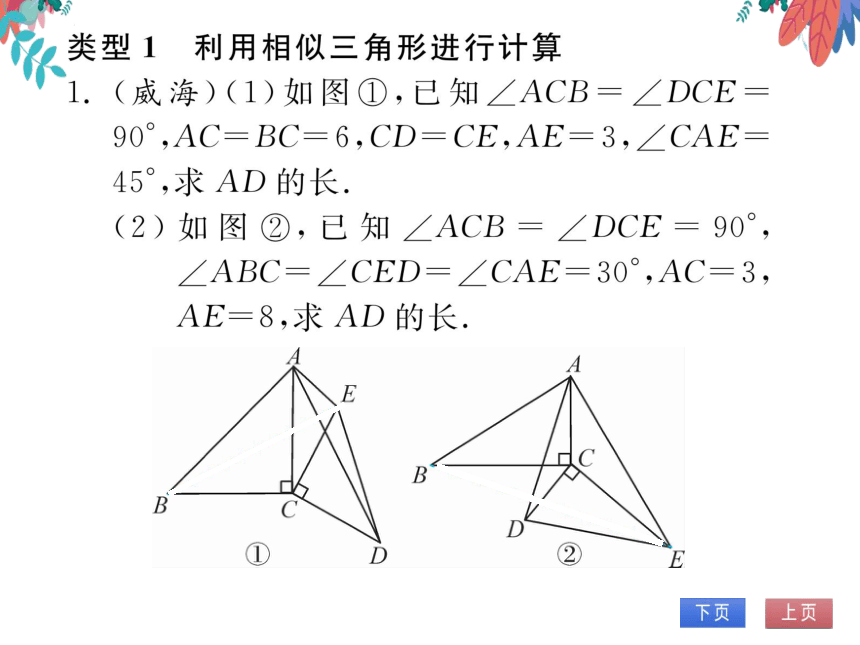
类型1利用相似三角形进行计算
(威海)(1)如图①,已知∠ACB=∠DCE
90,AC=BC=6, CD=Ce, AE=3, CAE
45°,求AD的长
(2)如图②,已知∠ACB=∠DCE=90
∠ABC=∠CED=∠CAE=30°,AC=3
AE=8,求AD的长
E
B
B
D
解:(1)如图①,连接BE,
∠ACB=∠DCE=90°,
ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD
又∵AC=BC,DC=EC,在△ACD和△BCE中
AC- BC
ACD=∠BCE,∴△ACD≌△BCE,∴AD=BE
DC-EC
AC=BC=6,∴AB=6√2,
∠BAC
CAE=45
∠BAE=90°,在Rt△BAE中,AB=62,AE=3,
BE=9,∴AD=9
(2)如图②,连接BE,在Rt△ABC与Rt△CDE中
ABC
CED=30°,
..AC
AB DC
123
DE
..AC
BC. CD
CE
AC
BC CE
又∵∠BCE=∠ACD
△ACD∽△BCE,
AD AC
BE BO
∠BAC=60°,∠CAE=30
∠BAE=90°,又∵AB=6,AE=8
BE=10,:An103
2.(邵阳)如图1所示,在四边形ABCD中,点O,
E,F,G,分别是AB,BC,CD,AD的中点,连
接OE,EF,FG,GO,GE
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,
如图2所示,连接GM,EN①若OE=√3,
EN
OG=1,求的值;②试在四边ABCD中添
加一个条件,使GM,EN的长在旋转过程中
始终相等.(不要求证明)
C
C
DGA
E
E
B
图1
图2N
解:(1)如图1,连接A
GF∥AC,OE∥-AC
GFOE,∴四边形OEFG为平行四边形
(2)①可证△OGM∽△OEN
EN OE
GM OC
②如图2,连接AC,BD,根据①知,△OGM△OEN
若要GM=EN,只需使△OGM9△OEN
所以需添加使AC=BD的条件均可以满足此条件
图,M为线段AB的中点,AE与BD交于点
C,∠DME=∠A=∠B=a,且DM交AC于
F,ME交BC于G
(1)写出图中三对相似三角形,并证明其中的
对
(2)连接FG,如果a=45°,AB=42,AF=3
求FC和FG的长
A
M
D
解:(1)△AME∽△MFE
△BMD∽△MGD
△AMF∽△BGM
选△AMF∽△BGM,
∠AMD=∠B+∠D
BGM
DMG+∠D
类型1利用相似三角形进行计算
(威海)(1)如图①,已知∠ACB=∠DCE
90,AC=BC=6, CD=Ce, AE=3, CAE
45°,求AD的长
(2)如图②,已知∠ACB=∠DCE=90
∠ABC=∠CED=∠CAE=30°,AC=3
AE=8,求AD的长
E
B
B
D
解:(1)如图①,连接BE,
∠ACB=∠DCE=90°,
ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD
又∵AC=BC,DC=EC,在△ACD和△BCE中
AC- BC
ACD=∠BCE,∴△ACD≌△BCE,∴AD=BE
DC-EC
AC=BC=6,∴AB=6√2,
∠BAC
CAE=45
∠BAE=90°,在Rt△BAE中,AB=62,AE=3,
BE=9,∴AD=9
(2)如图②,连接BE,在Rt△ABC与Rt△CDE中
ABC
CED=30°,
..AC
AB DC
123
DE
..AC
BC. CD
CE
AC
BC CE
又∵∠BCE=∠ACD
△ACD∽△BCE,
AD AC
BE BO
∠BAC=60°,∠CAE=30
∠BAE=90°,又∵AB=6,AE=8
BE=10,:An103
2.(邵阳)如图1所示,在四边形ABCD中,点O,
E,F,G,分别是AB,BC,CD,AD的中点,连
接OE,EF,FG,GO,GE
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,
如图2所示,连接GM,EN①若OE=√3,
EN
OG=1,求的值;②试在四边ABCD中添
加一个条件,使GM,EN的长在旋转过程中
始终相等.(不要求证明)
C
C
DGA
E
E
B
图1
图2N
解:(1)如图1,连接A
GF∥AC,OE∥-AC
GFOE,∴四边形OEFG为平行四边形
(2)①可证△OGM∽△OEN
EN OE
GM OC
②如图2,连接AC,BD,根据①知,△OGM△OEN
若要GM=EN,只需使△OGM9△OEN
所以需添加使AC=BD的条件均可以满足此条件
图,M为线段AB的中点,AE与BD交于点
C,∠DME=∠A=∠B=a,且DM交AC于
F,ME交BC于G
(1)写出图中三对相似三角形,并证明其中的
对
(2)连接FG,如果a=45°,AB=42,AF=3
求FC和FG的长
A
M
D
解:(1)△AME∽△MFE
△BMD∽△MGD
△AMF∽△BGM
选△AMF∽△BGM,
∠AMD=∠B+∠D
BGM
DMG+∠D
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
