【北师大版】数学九年级上册 1.3 第1课时—正方形的性质 习题课件
文档属性
| 名称 | 【北师大版】数学九年级上册 1.3 第1课时—正方形的性质 习题课件 |  | |
| 格式 | pptx | ||
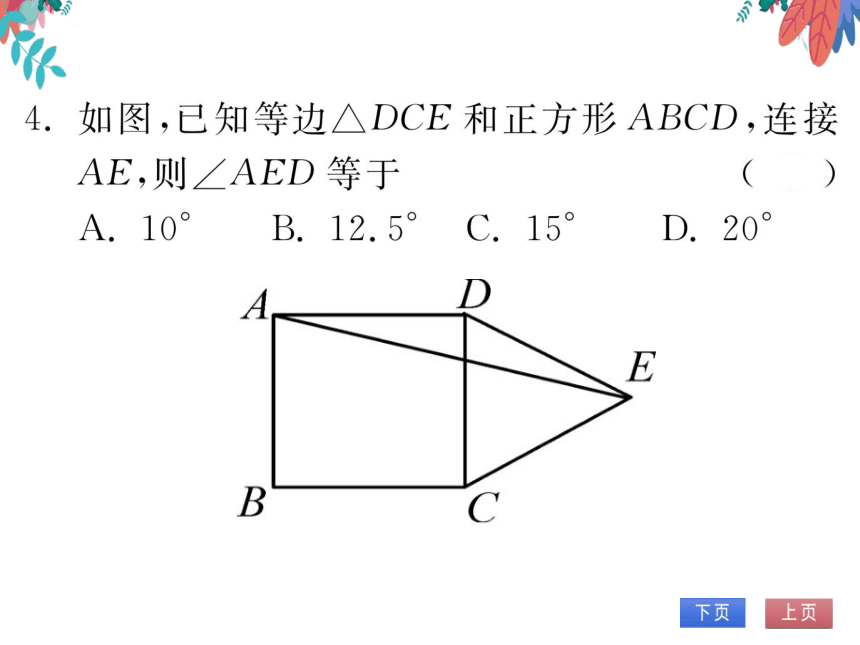
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:13:37 | ||
图片预览






文档简介
(共27张PPT)
N课前预习
预习新知
1.正方形的定义:有一组邻边相等,并且有
个角是直角的平行四边形叫做正方形
2.正方形既是矩形,又是菱形,它具有矩形
与菱形的所有性质
正方形的四个角都是直角,四条边相等
4.正方形的对角线相等且互相垂直平分
堂训练
巩固基础
知识点1正方形的定义
1.已知□ABCD中,AB=BC,若要使□ABCD
是正方形,则必须再添加一个条件可以是
A.∠A=90
B. BC=CD
C. AC BD
D.AB∥CD
知识点2正方形的性质
2.正方形具有而菱形不一定具有的性质是(C
A.四条边都相等
B.对角线互相垂直平分
C.对角线相等
D.对角线平分一组对角
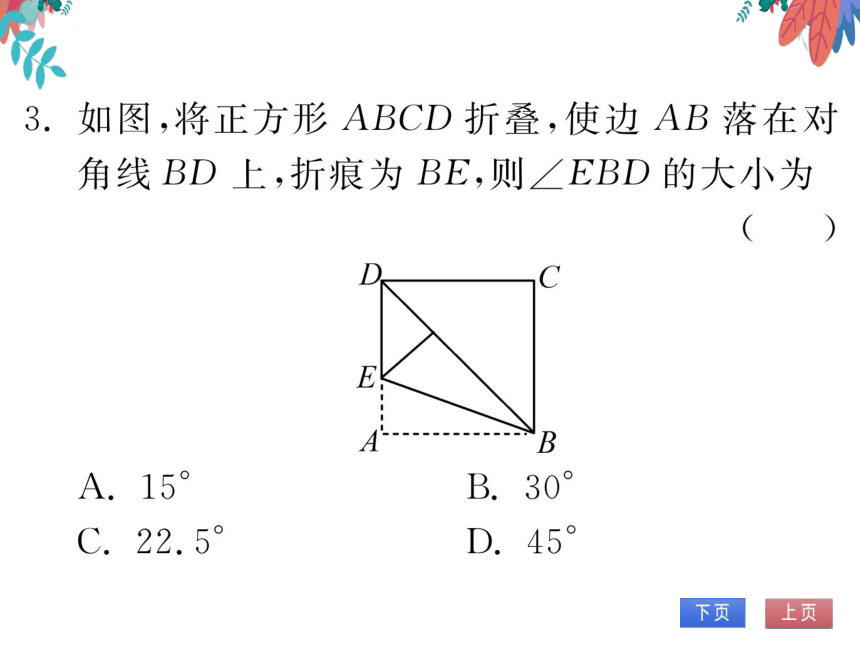
如图,将正方形ABCD折叠,使边AB落在对
角线BD上,折痕为BE,则∠EBD的大小为
E
B
B.30
B
(第4题图
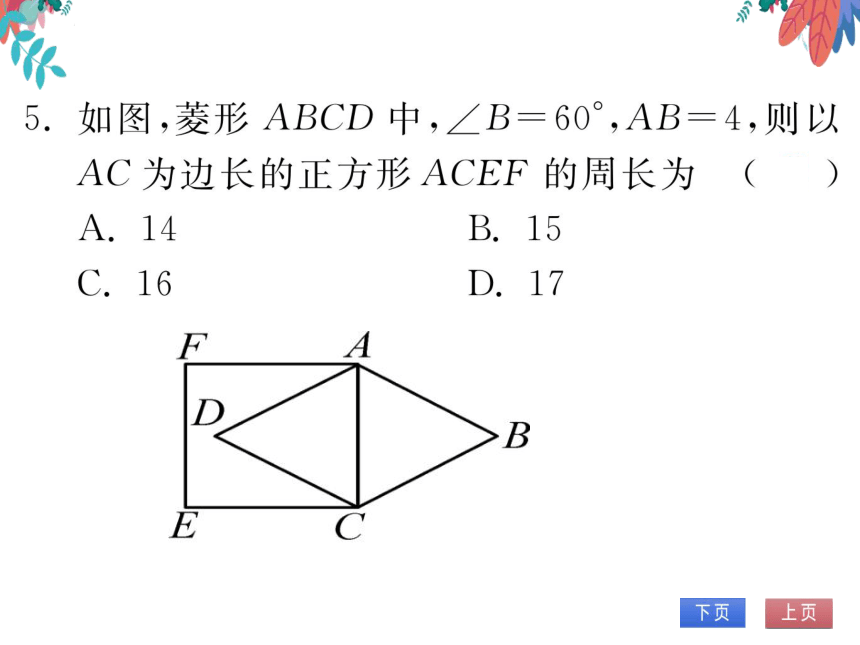
5.如图,菱形ABCD中,∠B=60°,AB=4,则以
AC为边长的正方形ACEF的周长为
A.14
B.15
第5题图
(枣庄)如图,把正方形纸片ABCD沿对边中
点所在的直线对折后展开,折痕为MN,再过
点B折叠纸片,使点A落在MN上的点F处
折痕为BE.若AB的长为2,则FM的长为
B
B.√3
B E
(第7题图)
C
E
B F
(第8题图)
D
B E
(第9题图)
0.如图,在正方形ABCD中,E是AB上一点
F是AD延长线上一点,且DF=BE
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE
BE+GD成立吗 为什么
D
EB
(1)证明:∵四边形ABCD为正
方形
∠B=∠BCD=∠CDA=90
CDF,且BC=CD
又∵BE=DF,∴.Rt△BCE≌
Rt△DCF
2)解:由(1)知:
BCE+∠ECD=∠ECD+∠FCD=90°
又∵∠GCE=45°,∴∠FCG=45°,
△ECG≌△FCG
GE=GF=GD+DF=GD+BE
课后作业
全面提升
1.(襄阳)“赵爽弦图”巧妙地利用面积关系证明
了勾股定理,是我国古代数学的骄傲,如图所
示的“赵爽弦图”是由四个全等的直角三角形
和一个小正方形拼成的一个大正方形,设直角
三角形较长直角边长为a,较短直角边长为b,
若(a+b)2=21,大正方形的面积为13,则小正
方形的面积为
(第1题图)
如图,点G是正方形ABCD对角线CA的延长
线上任意一点,以线段AG为边作一个正方形
AEFG,线段EB和GD相交于点H,且AB
2,AG=1,则BE
N课前预习
预习新知
1.正方形的定义:有一组邻边相等,并且有
个角是直角的平行四边形叫做正方形
2.正方形既是矩形,又是菱形,它具有矩形
与菱形的所有性质
正方形的四个角都是直角,四条边相等
4.正方形的对角线相等且互相垂直平分
堂训练
巩固基础
知识点1正方形的定义
1.已知□ABCD中,AB=BC,若要使□ABCD
是正方形,则必须再添加一个条件可以是
A.∠A=90
B. BC=CD
C. AC BD
D.AB∥CD
知识点2正方形的性质
2.正方形具有而菱形不一定具有的性质是(C
A.四条边都相等
B.对角线互相垂直平分
C.对角线相等
D.对角线平分一组对角
如图,将正方形ABCD折叠,使边AB落在对
角线BD上,折痕为BE,则∠EBD的大小为
E
B
B.30
B
(第4题图
5.如图,菱形ABCD中,∠B=60°,AB=4,则以
AC为边长的正方形ACEF的周长为
A.14
B.15
第5题图
(枣庄)如图,把正方形纸片ABCD沿对边中
点所在的直线对折后展开,折痕为MN,再过
点B折叠纸片,使点A落在MN上的点F处
折痕为BE.若AB的长为2,则FM的长为
B
B.√3
B E
(第7题图)
C
E
B F
(第8题图)
D
B E
(第9题图)
0.如图,在正方形ABCD中,E是AB上一点
F是AD延长线上一点,且DF=BE
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE
BE+GD成立吗 为什么
D
EB
(1)证明:∵四边形ABCD为正
方形
∠B=∠BCD=∠CDA=90
CDF,且BC=CD
又∵BE=DF,∴.Rt△BCE≌
Rt△DCF
2)解:由(1)知:
BCE+∠ECD=∠ECD+∠FCD=90°
又∵∠GCE=45°,∴∠FCG=45°,
△ECG≌△FCG
GE=GF=GD+DF=GD+BE
课后作业
全面提升
1.(襄阳)“赵爽弦图”巧妙地利用面积关系证明
了勾股定理,是我国古代数学的骄傲,如图所
示的“赵爽弦图”是由四个全等的直角三角形
和一个小正方形拼成的一个大正方形,设直角
三角形较长直角边长为a,较短直角边长为b,
若(a+b)2=21,大正方形的面积为13,则小正
方形的面积为
(第1题图)
如图,点G是正方形ABCD对角线CA的延长
线上任意一点,以线段AG为边作一个正方形
AEFG,线段EB和GD相交于点H,且AB
2,AG=1,则BE
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
