【华师大版】数学九年级上册 23.3.1 相似三角形 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 23.3.1 相似三角形 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:11:55 | ||
图片预览





文档简介
(共22张PPT)
课前预习
预习新知
1.相似用符号“∽”来表示,读作“相似于”
△ABC与△ABC′相似,记作△ABCC
△ABC.相似三角形对应边的比叫做相
似比;当相似比为1时,两个三角形为全等
角形.相似三角形的对应边成比例,对应
角相等
2.平行于三角形一边的直线,和其他两边(或两
边的延长线)相交所构成的三角形与原三角形
相似
当堂训练
巩固基础
知识点1相似三角形的性质及有关概念
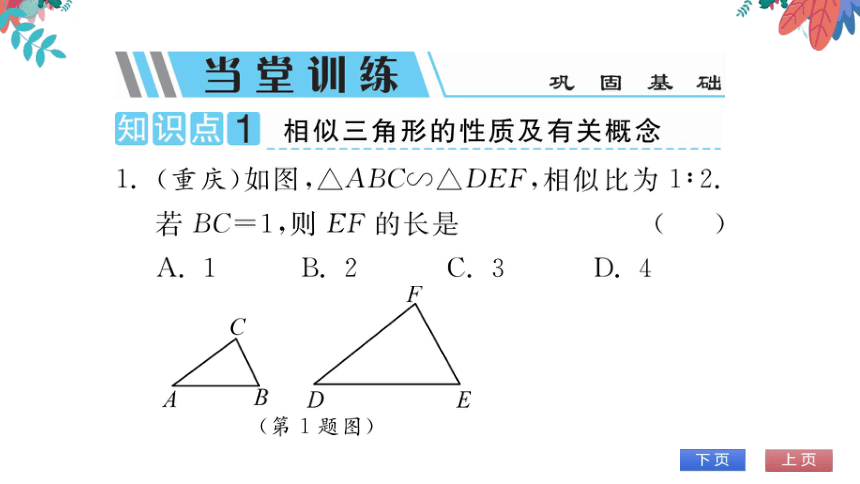
1.(重庆)如图,△ABC∽△DEF,相似比为1:2
若BC=1,则EF的长是
B
A
B.2
D.4
B D
E
(第1题图)
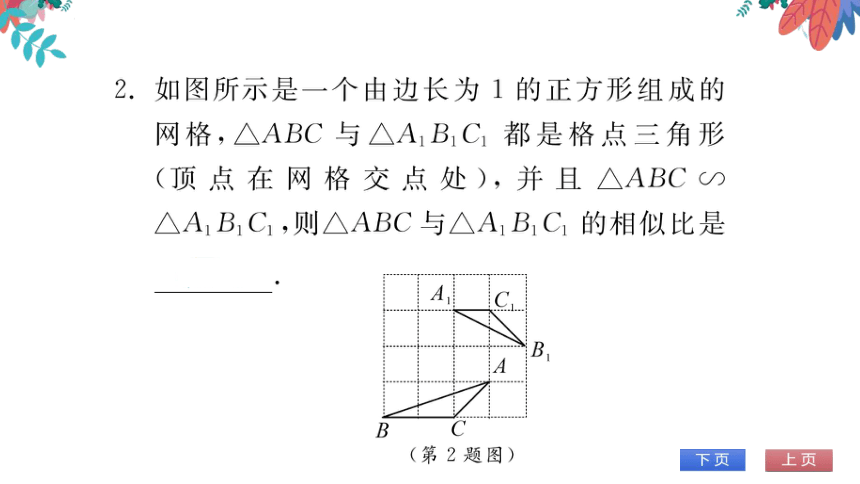
2.如图所示是一个由边长为1的正方形组成的
网格,△ABC与△A1B1C1都是格点三角形
(顶点在网格交点处),并且△ABCC
△A1B1C1,则△ABC与△A1B1C1的相似比是
2:1
C
B
B
(第2题图)
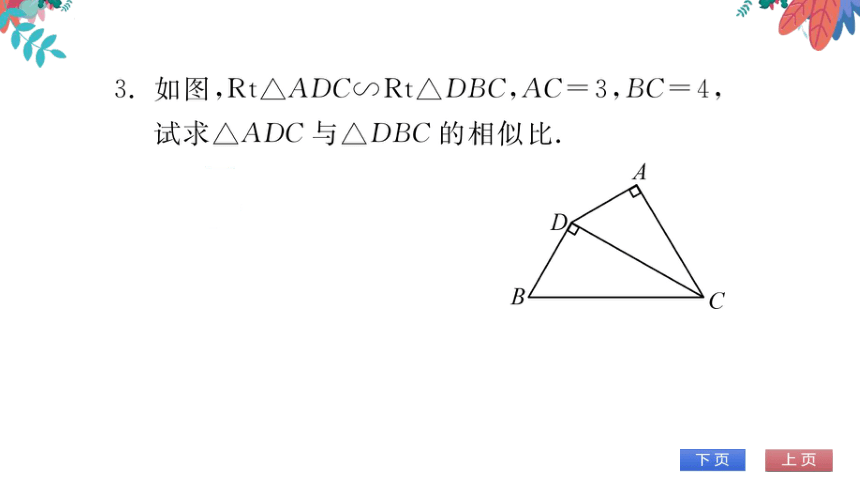
3.如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,
试求△ADC与△DBC的相似比
解
知识点2对应边、对应角的识别
4.在△ABC中,∠A=45°,∠B=35,则与△ABC
相似的三角形三个角的度数分别为
A.35°,45°,45°
B.45°,105°,35°
C.45,35°,110°
D.45°,35°,100°
A.∠F=50°,AB与DE是对应边
B.∠F=50°,AB与EF是对应边
C.∠F=50°,AB与DF是对应边
D.AB与DE,AC与DF,BC与EF是三组对应边
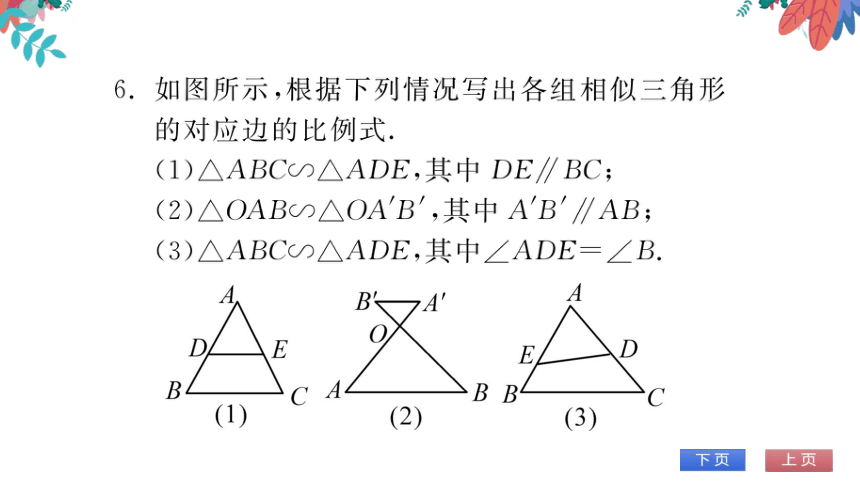
阳图所示,根据下列情况写出各组相似三角形
的对应边的比例式
(1)△ABC∽△ADE,其中DE∥BC
(2)△OAB∽△OAB,其中AB∥AB;
(3)△ABC∽△ADE,其中∠ADE=∠B
B\7A
E
E
B
A
BB
C
(2)
AD AE DE
解:(1)
AB AC BC
AO BO AB
(2)
AO BO AB
AD AE DE
(3)
AB AC BC
知识点3由平行线判定两个三角形相似
7.如图,平行四边形ABCD中,4
过点B的直线与对角线AC、
E
边AD分别交于点E和F,
B
过点E作EG∥BC,交AB于点G,则图中的
相似三角形有
(B)
A.4对B.5对
C.6劝
D.7对
8.如图,DE∥BC
(1)如果AD=2,DB=3,则DE:BC=2:5;
(2)如果AD=8,DB=12,AC=15,DE=7,求
AE和BC的长
课前预习
预习新知
1.相似用符号“∽”来表示,读作“相似于”
△ABC与△ABC′相似,记作△ABCC
△ABC.相似三角形对应边的比叫做相
似比;当相似比为1时,两个三角形为全等
角形.相似三角形的对应边成比例,对应
角相等
2.平行于三角形一边的直线,和其他两边(或两
边的延长线)相交所构成的三角形与原三角形
相似
当堂训练
巩固基础
知识点1相似三角形的性质及有关概念
1.(重庆)如图,△ABC∽△DEF,相似比为1:2
若BC=1,则EF的长是
B
A
B.2
D.4
B D
E
(第1题图)
2.如图所示是一个由边长为1的正方形组成的
网格,△ABC与△A1B1C1都是格点三角形
(顶点在网格交点处),并且△ABCC
△A1B1C1,则△ABC与△A1B1C1的相似比是
2:1
C
B
B
(第2题图)
3.如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,
试求△ADC与△DBC的相似比
解
知识点2对应边、对应角的识别
4.在△ABC中,∠A=45°,∠B=35,则与△ABC
相似的三角形三个角的度数分别为
A.35°,45°,45°
B.45°,105°,35°
C.45,35°,110°
D.45°,35°,100°
A.∠F=50°,AB与DE是对应边
B.∠F=50°,AB与EF是对应边
C.∠F=50°,AB与DF是对应边
D.AB与DE,AC与DF,BC与EF是三组对应边
阳图所示,根据下列情况写出各组相似三角形
的对应边的比例式
(1)△ABC∽△ADE,其中DE∥BC
(2)△OAB∽△OAB,其中AB∥AB;
(3)△ABC∽△ADE,其中∠ADE=∠B
B\7A
E
E
B
A
BB
C
(2)
AD AE DE
解:(1)
AB AC BC
AO BO AB
(2)
AO BO AB
AD AE DE
(3)
AB AC BC
知识点3由平行线判定两个三角形相似
7.如图,平行四边形ABCD中,4
过点B的直线与对角线AC、
E
边AD分别交于点E和F,
B
过点E作EG∥BC,交AB于点G,则图中的
相似三角形有
(B)
A.4对B.5对
C.6劝
D.7对
8.如图,DE∥BC
(1)如果AD=2,DB=3,则DE:BC=2:5;
(2)如果AD=8,DB=12,AC=15,DE=7,求
AE和BC的长
