【华师大版】数学九年级上册 23.4中位线 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 23.4中位线 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:11:55 | ||
图片预览





文档简介
(共23张PPT)
23.4中位线
课前预习
预习新知
1.连结三角形两边中点的线段叫做三角形
的中位线
角形的中位线平行于第三边,并且等于第
三边的一半
三角形有三条中线,它们相交于一点
这个点就是三角形的重心,重心与一边中
点的连线的长是对应中线长的
堂训练
巩固基础
知识点1三角形的中位线
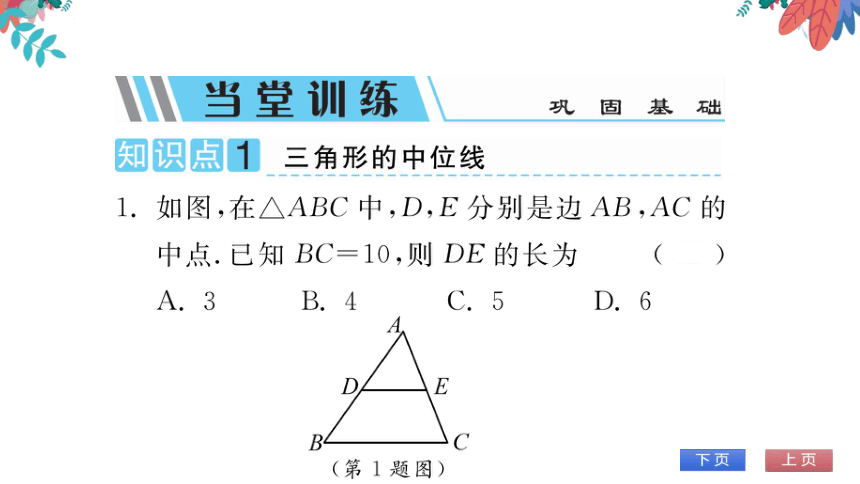
1.如图,在△ABC中,D,E分别是边AB,AC的
中点.已知BC=10,则DE的长为
E
B
C
(第1题图)
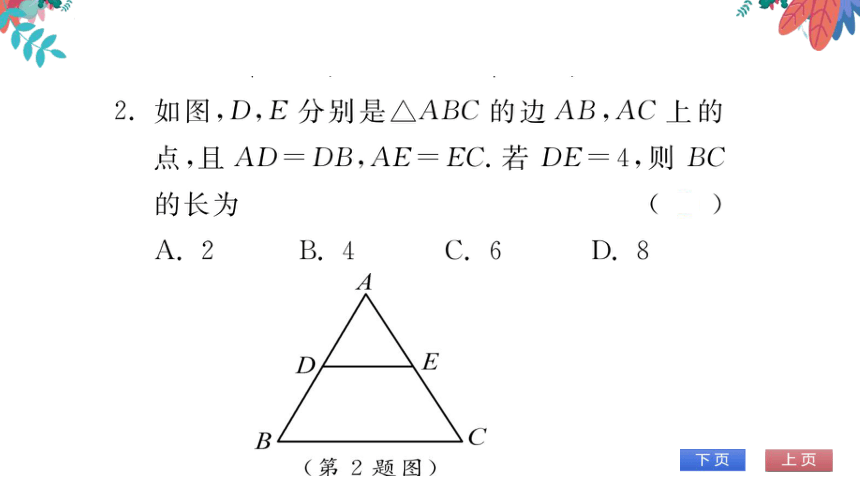
如图,D,E分别是△ABC的边AB,AC上的
点,且AD=DB,AE=EC.若DE=4,则BC
的长为
E
B
C
(第2题图
已知D,E,F分别是△ABC各边的中点,若
△ABC的周长是8cm,面积为6cm2,则△DEF
的周长是4cm,面积为
cm
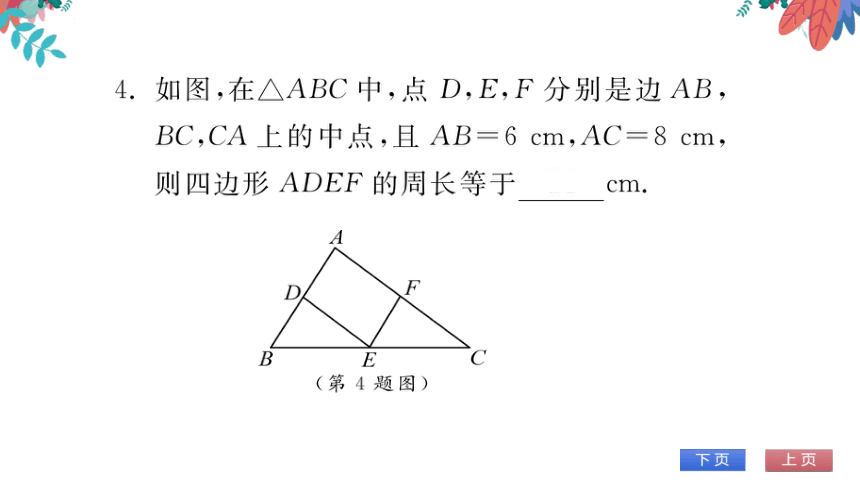
4.如图,在△ABC中,点D,E,F分别是边AB
BC,CA上的中点,且AB=6cm,AC=8cm
则四边形ADEF的周长等于14cm
B
E
第4题图)
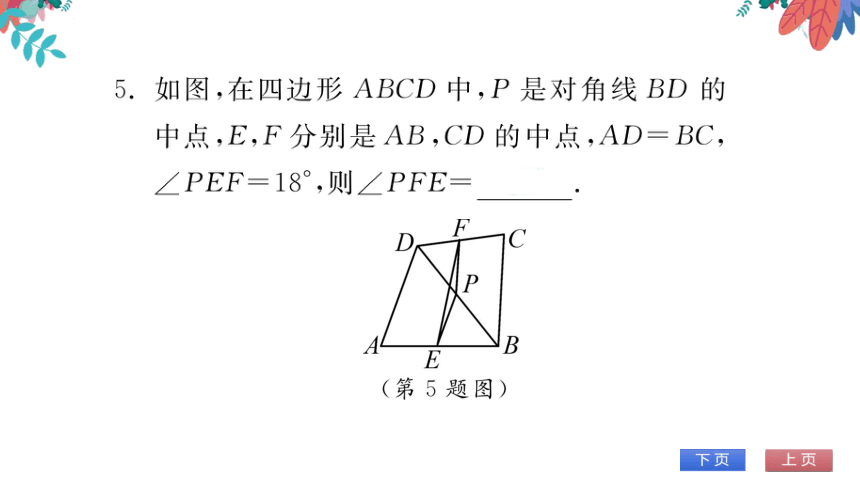
如图,在四边形ABCD中,P是对角线BD的
中点,E,F分别是AB,CD的中点,AD=BC
∠PEF=18°,则∠PFE=18°
C
P
B
E
(第5题图)
D,E分别是不等边三角形ABC(即AB≠
BC≠AC)的边AB,AC的中点.O是△ABC
所在平面上的动点,连结OB,OC,点G,F分
别是OB,OC的中点,顺次连结点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四
边形DEFG是平行四边形
2)若四边形DEFG是菱形,则OA与BC应
满足怎样的数量关系 (直接写出答案,不
需要说明理由
D
E
B
(1)证明:D,E分别是AB,
AC边的中点,
∴DE∥BC,且DE=7
BC
同理:GF∥BC,且GF=BC
DE∥GF且DE=GF
四边形DEFG是平行四边形
(2)解:当OA=BC时,四边形DEFG是菱形
知识点2三角形的重心
如图,在△ABC中,D,E分别为AB,AC的中
点,连结DE,线段BE,CD相交于点O.若
OD=2,则OC=4
E
B
8.如图,在△ABC中,G为重心,过点G的直线
MN∥AB,交AC于点M,交BC于点N,
AB=8,求MN的长
N
H
解:连结CG,并延长CG交
AB于点H
G是重心,MN∥AB
CG CM MN 2
CH CA AB 3
MN
课后作业
全面提升
1.(陕西)如图,在△ABC中,∠ABC=90°,AB
8,BC=6,若DE是△ABC的中位线,延长
DE交△ABC的外角∠ACM的平分线于点
F,则线段DF的长为
(B
D.10
23.4中位线
课前预习
预习新知
1.连结三角形两边中点的线段叫做三角形
的中位线
角形的中位线平行于第三边,并且等于第
三边的一半
三角形有三条中线,它们相交于一点
这个点就是三角形的重心,重心与一边中
点的连线的长是对应中线长的
堂训练
巩固基础
知识点1三角形的中位线
1.如图,在△ABC中,D,E分别是边AB,AC的
中点.已知BC=10,则DE的长为
E
B
C
(第1题图)
如图,D,E分别是△ABC的边AB,AC上的
点,且AD=DB,AE=EC.若DE=4,则BC
的长为
E
B
C
(第2题图
已知D,E,F分别是△ABC各边的中点,若
△ABC的周长是8cm,面积为6cm2,则△DEF
的周长是4cm,面积为
cm
4.如图,在△ABC中,点D,E,F分别是边AB
BC,CA上的中点,且AB=6cm,AC=8cm
则四边形ADEF的周长等于14cm
B
E
第4题图)
如图,在四边形ABCD中,P是对角线BD的
中点,E,F分别是AB,CD的中点,AD=BC
∠PEF=18°,则∠PFE=18°
C
P
B
E
(第5题图)
D,E分别是不等边三角形ABC(即AB≠
BC≠AC)的边AB,AC的中点.O是△ABC
所在平面上的动点,连结OB,OC,点G,F分
别是OB,OC的中点,顺次连结点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四
边形DEFG是平行四边形
2)若四边形DEFG是菱形,则OA与BC应
满足怎样的数量关系 (直接写出答案,不
需要说明理由
D
E
B
(1)证明:D,E分别是AB,
AC边的中点,
∴DE∥BC,且DE=7
BC
同理:GF∥BC,且GF=BC
DE∥GF且DE=GF
四边形DEFG是平行四边形
(2)解:当OA=BC时,四边形DEFG是菱形
知识点2三角形的重心
如图,在△ABC中,D,E分别为AB,AC的中
点,连结DE,线段BE,CD相交于点O.若
OD=2,则OC=4
E
B
8.如图,在△ABC中,G为重心,过点G的直线
MN∥AB,交AC于点M,交BC于点N,
AB=8,求MN的长
N
H
解:连结CG,并延长CG交
AB于点H
G是重心,MN∥AB
CG CM MN 2
CH CA AB 3
MN
课后作业
全面提升
1.(陕西)如图,在△ABC中,∠ABC=90°,AB
8,BC=6,若DE是△ABC的中位线,延长
DE交△ABC的外角∠ACM的平分线于点
F,则线段DF的长为
(B
D.10
