【华师大版】数学九年级上册 24.1 测量 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 24.1 测量 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第24章解直角三角形
24.1测
N课前预习
预习新知
利用物体在太阳光下的影子进行测量的根据
是在同一时刻,物高与影长成正比例
2.利用直角三角形进行测量的根据是勾股
定理,其内容是直角三角形的直角边的平方和
等于斜边的平方
3.构造相似三角形进行测量的根据是相似三角
形的对应角相等,对应边成比例
当堂训练
巩固基础
知识点1利用同一时刻物高与影长成比例测量
1.在同一时刻,测得小华和旗杆的影长分别为
1m和6m,小华的身高约为1.6m,则旗杆的
高约为
A.8.6m
B.
D.10
2.如图,身高为1.6m的某学生测量学校旗杆的
高度,当他站在C处时,他头顶端的影子正好
与旗杆顶端的影子重合,并测得AC=2.0m,
BC=8.0m,则旗杆的高度是
0
B
(第2题图)
知识点2利用勾股定理测量
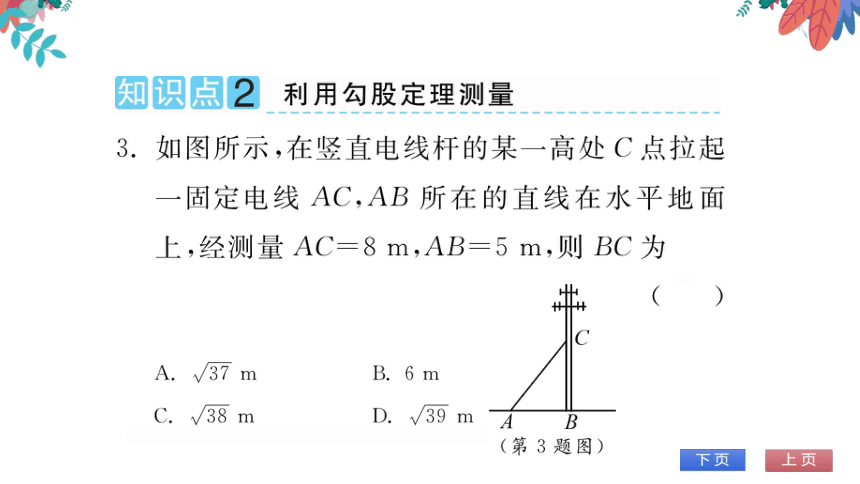
如图所示,在竖直电线杆的某一高处C点拉起
固定电线AC,AB所在的直线在水平地面
上,经测量AC=8m,AB=5m,则BC为
A.√37
B6 m
C.√38
D
第
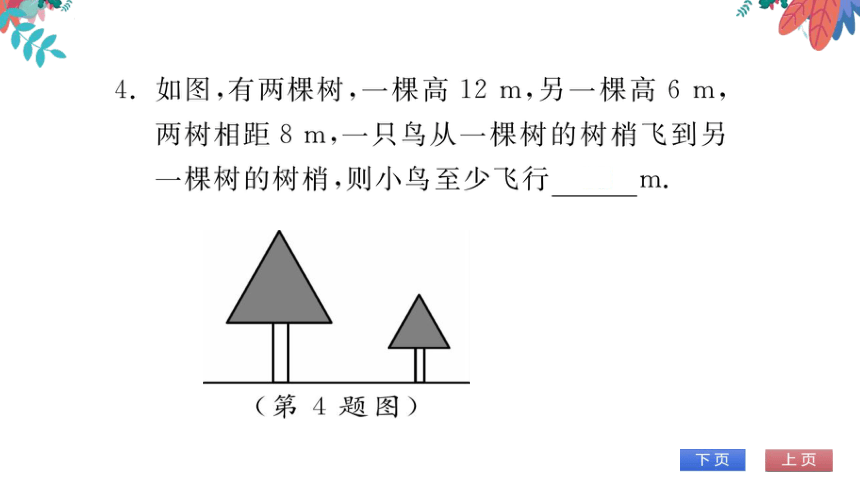
4.如图,有两棵树,一棵高12m,另一棵高6m
两树相距8m,一只鸟从一棵树的树梢飞到另
棵树的树梢,则小鸟至少飞行10m
(第4题图)
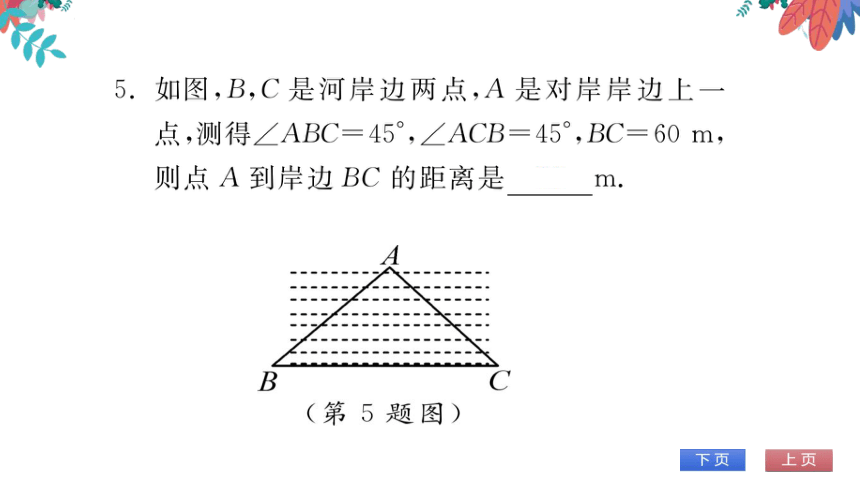
图,B,C是河岸边两点,A是对岸岸边上
点,测得∠ABC=45°,∠ACB=45°,BC=60m
则点A到岸边BC的距离是30m
B
(第5题图)
知识点3利用相似三角形的性质测量
6.小明在一次军事夏令营活动中,进行打靶训
练,在用枪瞄准目标点B时,要使眼睛O、准星
A、目标B在同一条直线上,如图所示,在射
击时,小明有轻微的抖动,致使准星A偏离到
A,若OA=0.2m,OB=40m,AA=0.0015m
则小明射击到的点B偏离目标点B的长度
BB′为
B
B
0.03mD.0.2
图,一人拿着
12cm长的直尺,站在距
离电线杆约为30m的地方,把手臂向前伸直
直尺竖直,看到直尺恰好遮住了电线杆,已知
他的手臂的长约为60cm,求电线杆的高度
A D
E
解:设电线杆的高度为xm
DE∥CB,∴△ADEC
0.12
△ACB.由题意,得
0.6
解得x=6,经检验,x=6是原分式方程
30
的解
答:电线杆的高度是6m
课后作业
全面提升
1.如图①,某温室屋顶结构外框为△ABC,立柱
AD垂直平分横梁BC,AD=2m,斜梁AC
4m,为增大向阳面的面积,将立柱增高并改
第24章解直角三角形
24.1测
N课前预习
预习新知
利用物体在太阳光下的影子进行测量的根据
是在同一时刻,物高与影长成正比例
2.利用直角三角形进行测量的根据是勾股
定理,其内容是直角三角形的直角边的平方和
等于斜边的平方
3.构造相似三角形进行测量的根据是相似三角
形的对应角相等,对应边成比例
当堂训练
巩固基础
知识点1利用同一时刻物高与影长成比例测量
1.在同一时刻,测得小华和旗杆的影长分别为
1m和6m,小华的身高约为1.6m,则旗杆的
高约为
A.8.6m
B.
D.10
2.如图,身高为1.6m的某学生测量学校旗杆的
高度,当他站在C处时,他头顶端的影子正好
与旗杆顶端的影子重合,并测得AC=2.0m,
BC=8.0m,则旗杆的高度是
0
B
(第2题图)
知识点2利用勾股定理测量
如图所示,在竖直电线杆的某一高处C点拉起
固定电线AC,AB所在的直线在水平地面
上,经测量AC=8m,AB=5m,则BC为
A.√37
B6 m
C.√38
D
第
4.如图,有两棵树,一棵高12m,另一棵高6m
两树相距8m,一只鸟从一棵树的树梢飞到另
棵树的树梢,则小鸟至少飞行10m
(第4题图)
图,B,C是河岸边两点,A是对岸岸边上
点,测得∠ABC=45°,∠ACB=45°,BC=60m
则点A到岸边BC的距离是30m
B
(第5题图)
知识点3利用相似三角形的性质测量
6.小明在一次军事夏令营活动中,进行打靶训
练,在用枪瞄准目标点B时,要使眼睛O、准星
A、目标B在同一条直线上,如图所示,在射
击时,小明有轻微的抖动,致使准星A偏离到
A,若OA=0.2m,OB=40m,AA=0.0015m
则小明射击到的点B偏离目标点B的长度
BB′为
B
B
0.03mD.0.2
图,一人拿着
12cm长的直尺,站在距
离电线杆约为30m的地方,把手臂向前伸直
直尺竖直,看到直尺恰好遮住了电线杆,已知
他的手臂的长约为60cm,求电线杆的高度
A D
E
解:设电线杆的高度为xm
DE∥CB,∴△ADEC
0.12
△ACB.由题意,得
0.6
解得x=6,经检验,x=6是原分式方程
30
的解
答:电线杆的高度是6m
课后作业
全面提升
1.如图①,某温室屋顶结构外框为△ABC,立柱
AD垂直平分横梁BC,AD=2m,斜梁AC
4m,为增大向阳面的面积,将立柱增高并改
