【华师大版】数学九年级上册 第21章 专题一 二次根式的性质及其运算 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 第21章 专题一 二次根式的性质及其运算 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览





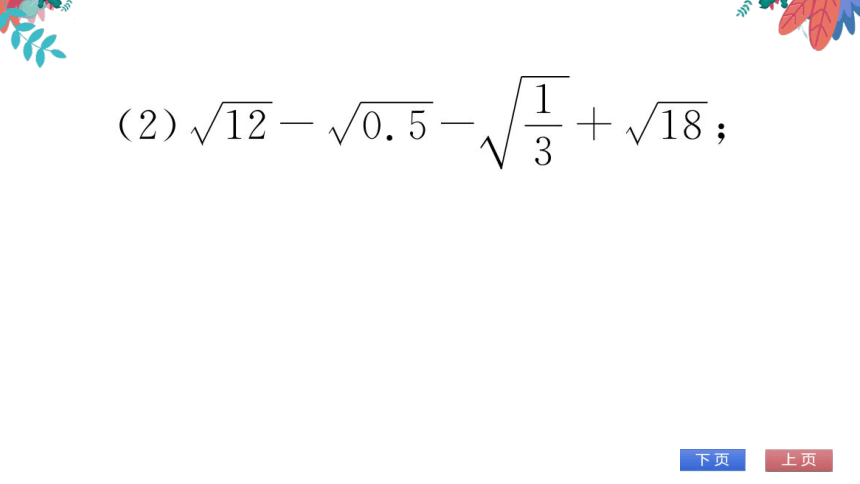
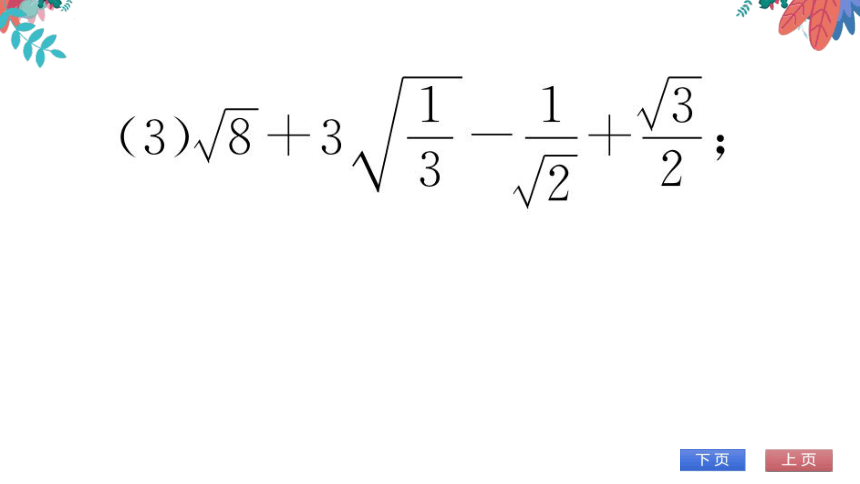
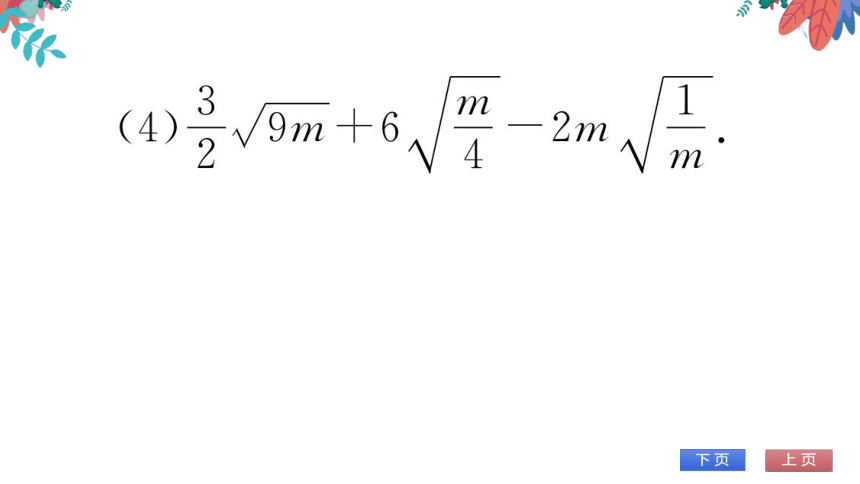

文档简介
(共20张PPT)
类型1二次根式定义的应用
下列式子不一定是二次根式的是
3x(x≤0)
8x-16
3.无论x取任何实数,代数式√x2-4x+m都有
意义,化简式子√(m-3)2+√(4-m)2
解:∴x2-4x+m
x-2)2+m-4且无论
x取任何实数,代数式√x2-4x+m都有意
义
72
≥4.
√(m-3)2+√(4-m)2=(m-3)+(m-4)
类型2二次根式的非负性
4.若√3x-4-√4-3x
则3x
的值为2
5.已知√a-=5+(2b+3)2=0,则√abB2
6.已知
有意义,则点A(a,√-a)在第
象限
类型3二次根式的加减
计算
(1)2√75-3√27
解:原式=2×53-3×3√3+2√3
10√3-93+2√3
(2)√12
解:原式=3+√2
(3)
3
解:原式=。2+3
(4)2√9m+6
72
4
11
解:原式
√72
类型4二次根式的乘除
计算
(1)√27×
解:原式=12
(2)/2
(3√28)×(-5/2
解:原式
16
328
116
2287
49
170
21
(341
解:原式=3×
15
5
解:原式=2
2×
2
类型5二次根式的混合运算
计算:
(1)(大连)3(1√3)+√12
(3)(呼和浩特)2
2×
解:原式=5-2
2√5-1
类型6二次根式探索规律题
10.观察一组数据并寻找规律:0,3,6,3,2√3,
5,3√2,…,猜想第n个数据是多少
解:观察发现已知数据可以变为√3×0
3
3×2
3
3×4
3×5
×6
所以第n个数据是√3(n-1)
1.小明在学习二次根式后,发现一些含根号的
式子可以写成另一个式子的平方,如3
2√2=(1+√2)2.善于思考的小明进行了以
下探索:
设a+b√2=(m+n√2)2(a,b,m,n均为整
数),则有a+b√2=m2+22+2m√2
a=m2+2n2,b=2mn.这样小明就找到了
种把类似a+b√2的式子化为平方式的
方法
请你仿照小明的方法探索并解决下列问题:
(1)a,b,m,n均为正整数时,若a+b√3
(m+n3)2,用含m,n的式子分别表示
b,得
b
(2)利用所探索的结论,用一组正整数a,b
填空
3)若a+4√3=(m+n3)2,且a,m,n均为
正整数,求a的值
解:(1)∵a+b√3=(m+n3)2
b/3
2m3,
3n2,b=2m
(2)设m-1,n=1
则a=m2+3n2=4,b=2mn=2
故填4,2,1,1.(答案不唯一,合理即可)
(3)由(1)得a=m2+372,b=2m
4=2mn,且m,n均为正整数,
m=2,n=1或m=1,n=2,
a=22+3×12=7划a=12+3×22=13
类型1二次根式定义的应用
下列式子不一定是二次根式的是
3x(x≤0)
8x-16
3.无论x取任何实数,代数式√x2-4x+m都有
意义,化简式子√(m-3)2+√(4-m)2
解:∴x2-4x+m
x-2)2+m-4且无论
x取任何实数,代数式√x2-4x+m都有意
义
72
≥4.
√(m-3)2+√(4-m)2=(m-3)+(m-4)
类型2二次根式的非负性
4.若√3x-4-√4-3x
则3x
的值为2
5.已知√a-=5+(2b+3)2=0,则√abB2
6.已知
有意义,则点A(a,√-a)在第
象限
类型3二次根式的加减
计算
(1)2√75-3√27
解:原式=2×53-3×3√3+2√3
10√3-93+2√3
(2)√12
解:原式=3+√2
(3)
3
解:原式=。2+3
(4)2√9m+6
72
4
11
解:原式
√72
类型4二次根式的乘除
计算
(1)√27×
解:原式=12
(2)/2
(3√28)×(-5/2
解:原式
16
328
116
2287
49
170
21
(341
解:原式=3×
15
5
解:原式=2
2×
2
类型5二次根式的混合运算
计算:
(1)(大连)3(1√3)+√12
(3)(呼和浩特)2
2×
解:原式=5-2
2√5-1
类型6二次根式探索规律题
10.观察一组数据并寻找规律:0,3,6,3,2√3,
5,3√2,…,猜想第n个数据是多少
解:观察发现已知数据可以变为√3×0
3
3×2
3
3×4
3×5
×6
所以第n个数据是√3(n-1)
1.小明在学习二次根式后,发现一些含根号的
式子可以写成另一个式子的平方,如3
2√2=(1+√2)2.善于思考的小明进行了以
下探索:
设a+b√2=(m+n√2)2(a,b,m,n均为整
数),则有a+b√2=m2+22+2m√2
a=m2+2n2,b=2mn.这样小明就找到了
种把类似a+b√2的式子化为平方式的
方法
请你仿照小明的方法探索并解决下列问题:
(1)a,b,m,n均为正整数时,若a+b√3
(m+n3)2,用含m,n的式子分别表示
b,得
b
(2)利用所探索的结论,用一组正整数a,b
填空
3)若a+4√3=(m+n3)2,且a,m,n均为
正整数,求a的值
解:(1)∵a+b√3=(m+n3)2
b/3
2m3,
3n2,b=2m
(2)设m-1,n=1
则a=m2+3n2=4,b=2mn=2
故填4,2,1,1.(答案不唯一,合理即可)
(3)由(1)得a=m2+372,b=2m
4=2mn,且m,n均为正整数,
m=2,n=1或m=1,n=2,
a=22+3×12=7划a=12+3×22=13
