【华师大版】数学九年级上册 第24章 专题七 解直角三角形的应用 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 第24章 专题七 解直角三角形的应用 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
类型1利用解直角三角形求河流的宽度
某同学在笔直的河岸BC进行数学实践活动,
如图,河对岸有一水站A,该同学在河岸B处
测得∠ABD=45°,沿河岸行走300m后到达
解:由题图可知AD⊥BC,
∠ABD=∠BAD=45°
在Rt△ABD中,BD=AD
在Rt△ACD中
C=30
AD
3AD
tan 3o
设AD=xm,则BD=xm,CD=3xm
依题意得BD+CD=300m,
300
300
≈110.故河宽AD约为110
处距离为99海里,可疑船只正沿南偏东53°方
向航行.我渔政船迅速沿北偏东27°方向前去
拦截,2小时后刚好在C处将可疑船只拦截,求
该可疑船只航行的速度.(参考数据:sin27°
4
COS27≈,tan27≈,si1n53≈,Cos53≈
20
4
,an53≈
解:如图,根据题意可得,在△ABC↑北
中,AB=99海里,∠ABC=53°,
BAC=27°,过点C作CD⊥AB,垂
足为点D,设BD=x海里,则AD
(99-x)海里,在Rt△BCD中
tan∠DBC=tan53CD
BD
4
CD=x·tan53°≈x(海里),在Rt△ACD
DO
tan∠DAC=tan2AD,则CD=AD
类型3利用解直角三角形求建筑物的高度
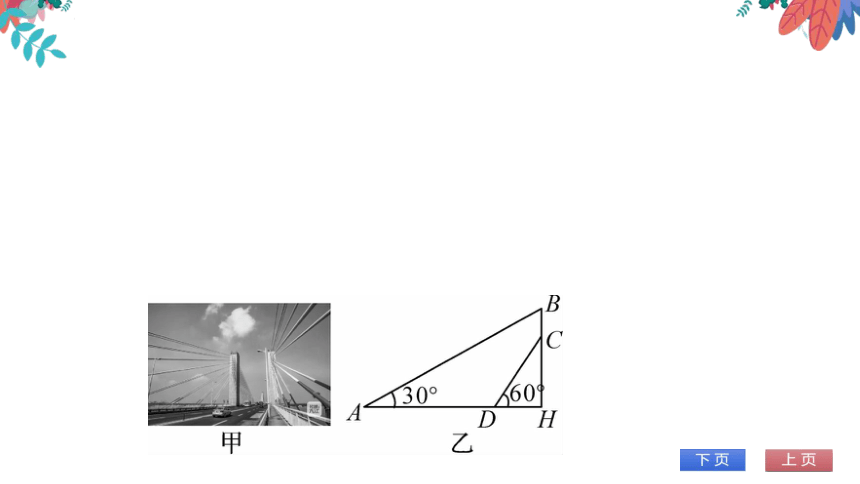
3.(娄底)芜湖长江大桥是中国跨度最大的公路
和铁路两用桥梁,大桥采用低塔斜拉桥桥型
图甲),图乙是从图甲引申出的平面图,假
设你站在桥上测得拉索AB与水平桥面的夹
角是30°,拉索CD与水平桥面的夹角是60
两拉索顶端的距离BC为2m,两拉索底端的
距离AD为20m,请求出立柱BH的长
(结果精确到0.1m,√3≈1.732)
B
∠30
60
甲
解:设DH=xm
CDH=60,∠H=90°,
CHEDH tango
BH=BC+CH-2+3x
A=30°
AH=√3BH=23+3x
AH=+ DH
23+3x=20+x
解得:x=10-3
BH=2+√3(10-3)
103-1≈16.3(m)
答:立柱BH的长约为16.3m
4.如图,某人在山坡坡脚C处测得一座建筑物顶
点A的仰角为60°,沿山坡向上走到P处再测
得该建筑物顶点A的仰角为45°.已知BC
90m,且B,C,D在同一条直线上,山坡坡度为
即tan∠PCD7
解:(1)如图,过点P作,A
PE⊥BD于E,PF⊥AB
于F
AB⊥BC于B,∴四边
山坡
形BEPF是矩形,
DOlF
∴PE=BF,PF=BE
60
在Rt△ABC中,BC
B
CED水平地面
90m,
∴∠ACB=60°,∴AB=BC·tan60°=90√3(m),故建筑
物的高度为903m
类型1利用解直角三角形求河流的宽度
某同学在笔直的河岸BC进行数学实践活动,
如图,河对岸有一水站A,该同学在河岸B处
测得∠ABD=45°,沿河岸行走300m后到达
解:由题图可知AD⊥BC,
∠ABD=∠BAD=45°
在Rt△ABD中,BD=AD
在Rt△ACD中
C=30
AD
3AD
tan 3o
设AD=xm,则BD=xm,CD=3xm
依题意得BD+CD=300m,
300
300
≈110.故河宽AD约为110
处距离为99海里,可疑船只正沿南偏东53°方
向航行.我渔政船迅速沿北偏东27°方向前去
拦截,2小时后刚好在C处将可疑船只拦截,求
该可疑船只航行的速度.(参考数据:sin27°
4
COS27≈,tan27≈,si1n53≈,Cos53≈
20
4
,an53≈
解:如图,根据题意可得,在△ABC↑北
中,AB=99海里,∠ABC=53°,
BAC=27°,过点C作CD⊥AB,垂
足为点D,设BD=x海里,则AD
(99-x)海里,在Rt△BCD中
tan∠DBC=tan53CD
BD
4
CD=x·tan53°≈x(海里),在Rt△ACD
DO
tan∠DAC=tan2AD,则CD=AD
类型3利用解直角三角形求建筑物的高度
3.(娄底)芜湖长江大桥是中国跨度最大的公路
和铁路两用桥梁,大桥采用低塔斜拉桥桥型
图甲),图乙是从图甲引申出的平面图,假
设你站在桥上测得拉索AB与水平桥面的夹
角是30°,拉索CD与水平桥面的夹角是60
两拉索顶端的距离BC为2m,两拉索底端的
距离AD为20m,请求出立柱BH的长
(结果精确到0.1m,√3≈1.732)
B
∠30
60
甲
解:设DH=xm
CDH=60,∠H=90°,
CHEDH tango
BH=BC+CH-2+3x
A=30°
AH=√3BH=23+3x
AH=+ DH
23+3x=20+x
解得:x=10-3
BH=2+√3(10-3)
103-1≈16.3(m)
答:立柱BH的长约为16.3m
4.如图,某人在山坡坡脚C处测得一座建筑物顶
点A的仰角为60°,沿山坡向上走到P处再测
得该建筑物顶点A的仰角为45°.已知BC
90m,且B,C,D在同一条直线上,山坡坡度为
即tan∠PCD7
解:(1)如图,过点P作,A
PE⊥BD于E,PF⊥AB
于F
AB⊥BC于B,∴四边
山坡
形BEPF是矩形,
DOlF
∴PE=BF,PF=BE
60
在Rt△ABC中,BC
B
CED水平地面
90m,
∴∠ACB=60°,∴AB=BC·tan60°=90√3(m),故建筑
物的高度为903m
