【华师大版】数学九年级上册 21.1 二次根式 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 21.1 二次根式 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:10:06 | ||
图片预览








文档简介
(共22张PPT)
第21章二次根式
21.1二次根式
N课前预习
预习新知
1.一般地,形如a(a≥0)的式子叫做二次
根式,在二次根式√a中,字母a必须满足
a≥0,即被开方数必须是非负数
2.对于二次根式a,有:(1a
0(a≥0);
(2)(√a)
a(a≥0).
3.√a2中的a为任意实数.(1)当a≥0时
a2=a;(2)当a<0时,√a2
堂训练
巩固基础
知识点1二次根式的定义
1.下列式子一定是二次根式的是
A
x-2
D
2.下列各式中,哪些是二次根式,哪些不是,为什么
16
7,(x≥0)
解
(x≥0)
是二次根式
7,√a-2不是二次根式.理由:3,√16,。(x
8符合二次根式的概念,故是二次根式,5的
根指数是3,故不是二次根式
7的被开方数小于0
无意义,故不是二次根式;√a-2的被开方数a-2不能
确定是否大于或等于0,故也不是二次根式
知识点2二次根式有意义的条件
3.(重庆)若二次根式√a=2有意义,则a的取值
范围是
A
D.a≠2
4.如果√x-1无意义,那么字母x的取值范围是
A.x≥1B.x>1C.x≤1D.x<1
5.(烟台)在函数y
中,自变量x的取值
范围是x≤1且x≠-2
写出下列各式有意义的条件
(2)
4
解
解:1≤a≤4
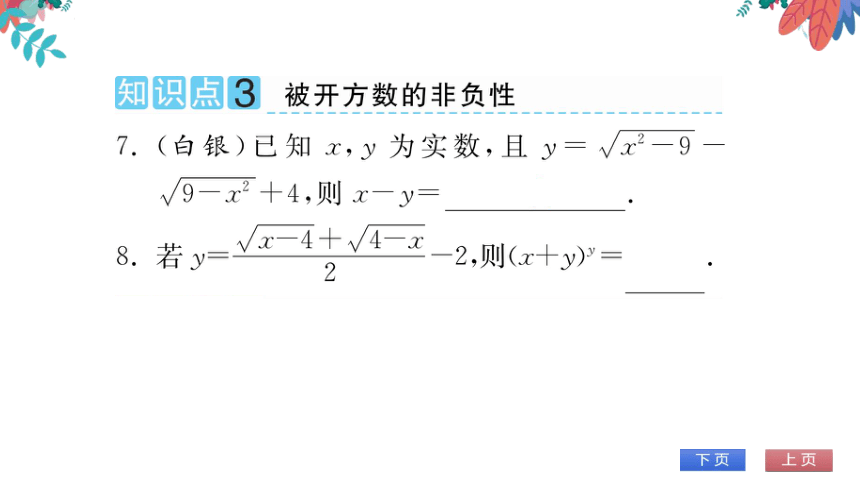
知识点3被开方数的非负性
(白银)已知x,y为实数,且y=√x2-9
1或-7
若
√x-4+√4-x
2,则(x+y)
4
知识点4二次根式的非负性
9.已知{a-2|+√7+b=0,则a+b的值为
B
D.9
10.若√x-1+(y+2)2=0,则(x+y)202等于
2020
D
2020
知识点5二次根式的性质
11.把4写成一个正数的平方的形式是(B
A.(2
4
C.(士2
D.(士入
4
2.下列计算正确的是
A.(√5)2=25
B
3)
3D.√O2=0
3.计算:√(-2)2
14.化简
)y(-2)
(2)(-2√3)
解
解:(-2√3)
22×3
课后作业
全面提升
1.当a为任意实数时,下列各式中是二次根式的
疋
(D)
1;②√5a2;③
A.①②③
B.②③④
D.②③
2.若√x-2+√3+y=0,则(x+y)209的值为
D.—1
(潍坊)实数a,b在数轴上对应点的位置如图
所示,化简a
(a-b)的结果是(A
0
atb
B. 2a-b
当x为何值时,代数式√x-3
有
意义
x-3≥0
x≥3
解:由题意得
解得
5-x>0,
第21章二次根式
21.1二次根式
N课前预习
预习新知
1.一般地,形如a(a≥0)的式子叫做二次
根式,在二次根式√a中,字母a必须满足
a≥0,即被开方数必须是非负数
2.对于二次根式a,有:(1a
0(a≥0);
(2)(√a)
a(a≥0).
3.√a2中的a为任意实数.(1)当a≥0时
a2=a;(2)当a<0时,√a2
堂训练
巩固基础
知识点1二次根式的定义
1.下列式子一定是二次根式的是
A
x-2
D
2.下列各式中,哪些是二次根式,哪些不是,为什么
16
7,(x≥0)
解
(x≥0)
是二次根式
7,√a-2不是二次根式.理由:3,√16,。(x
8符合二次根式的概念,故是二次根式,5的
根指数是3,故不是二次根式
7的被开方数小于0
无意义,故不是二次根式;√a-2的被开方数a-2不能
确定是否大于或等于0,故也不是二次根式
知识点2二次根式有意义的条件
3.(重庆)若二次根式√a=2有意义,则a的取值
范围是
A
D.a≠2
4.如果√x-1无意义,那么字母x的取值范围是
A.x≥1B.x>1C.x≤1D.x<1
5.(烟台)在函数y
中,自变量x的取值
范围是x≤1且x≠-2
写出下列各式有意义的条件
(2)
4
解
解:1≤a≤4
知识点3被开方数的非负性
(白银)已知x,y为实数,且y=√x2-9
1或-7
若
√x-4+√4-x
2,则(x+y)
4
知识点4二次根式的非负性
9.已知{a-2|+√7+b=0,则a+b的值为
B
D.9
10.若√x-1+(y+2)2=0,则(x+y)202等于
2020
D
2020
知识点5二次根式的性质
11.把4写成一个正数的平方的形式是(B
A.(2
4
C.(士2
D.(士入
4
2.下列计算正确的是
A.(√5)2=25
B
3)
3D.√O2=0
3.计算:√(-2)2
14.化简
)y(-2)
(2)(-2√3)
解
解:(-2√3)
22×3
课后作业
全面提升
1.当a为任意实数时,下列各式中是二次根式的
疋
(D)
1;②√5a2;③
A.①②③
B.②③④
D.②③
2.若√x-2+√3+y=0,则(x+y)209的值为
D.—1
(潍坊)实数a,b在数轴上对应点的位置如图
所示,化简a
(a-b)的结果是(A
0
atb
B. 2a-b
当x为何值时,代数式√x-3
有
意义
x-3≥0
x≥3
解:由题意得
解得
5-x>0,
