【华师大版】数学九年级上册 21.2.1 二次根式的乘法 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 21.2.1 二次根式的乘法 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:10:06 | ||
图片预览




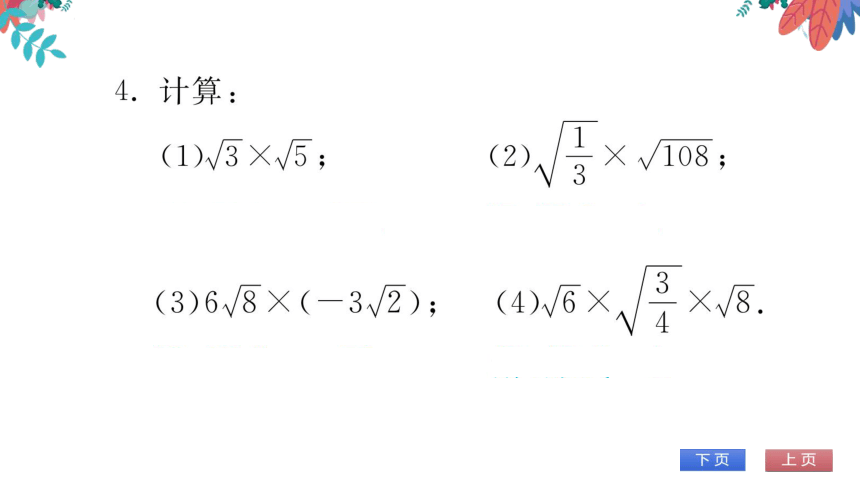

文档简介
(共12张PPT)
当堂训练
巩固基础
知识点1a·b=√ab成立的条件
1.若√a·√b=√ab成立,则下列说法正确的是
A.a≥0,b≥0
B.a>0,b>0
C.a≤b,b≤0
D.a<0,b<0
知识点2二次根式乘法法则的应用
3.下列等式成立的是
A.4√5×2√5=85B.53×4√2=20
C.4√3×3√2=7√
D.53×42=20√6
4.计算:
(1)3×√5
(2)/,×√108
解:原式=√15
解:原式=6
课后作业
全面提升
1.(杭州)已知m
√3
×(-2√21),则有
A.5B.4C.-54
D.-5计算
(1)°√20×(-√15)
48
解:原式
(
1)
20×15×48
120=60
(2)
Vab
(a>0,b>0)
125a
b
解:原式=5ab
125a
25
3.阅读下列解答过程,在括号中填入恰当的
内容
(1)由上述过程可知a的取值范围为≤0
(2)上述解答过程有错误的是第⑤步,正
确结果为
4.(河北)已知一个长方形花坛与一个圆形花坛
的面积相等,长方形花坛的长为√140πm,宽
为√35πm,求圆形花坛的半径r
解:长方形花坛的面积为√140×35
70π(m2).因为长方形花坛与圆形花坛的面积
相等,所以x2=70π.所以圆形花坛的半径r
70(
超越自我
比较前后两个算式计算结果的大小.(填
或
(1)2+
2×2×
(2)3+3
2×√3×√3;
(3)9+16
2×√9×√16;
通过观察与归纳,写出其中的规律,并说明
理由
解:(1)>(2)=(3)
规律:a+b≥2a·b(a≥0,b≥0)
理由:∵a=(a)2,b=(b)2(a≥0,b≥0)
a+b-2a·√b=(a)2-2a·√b+(b)
a+b≥2√a·√b(a≥0,b≥0)
当堂训练
巩固基础
知识点1a·b=√ab成立的条件
1.若√a·√b=√ab成立,则下列说法正确的是
A.a≥0,b≥0
B.a>0,b>0
C.a≤b,b≤0
D.a<0,b<0
知识点2二次根式乘法法则的应用
3.下列等式成立的是
A.4√5×2√5=85B.53×4√2=20
C.4√3×3√2=7√
D.53×42=20√6
4.计算:
(1)3×√5
(2)/,×√108
解:原式=√15
解:原式=6
课后作业
全面提升
1.(杭州)已知m
√3
×(-2√21),则有
A.5
D.-5
(1)°√20×(-√15)
48
解:原式
(
1)
20×15×48
120=60
(2)
Vab
(a>0,b>0)
125a
b
解:原式=5ab
125a
25
3.阅读下列解答过程,在括号中填入恰当的
内容
(1)由上述过程可知a的取值范围为≤0
(2)上述解答过程有错误的是第⑤步,正
确结果为
4.(河北)已知一个长方形花坛与一个圆形花坛
的面积相等,长方形花坛的长为√140πm,宽
为√35πm,求圆形花坛的半径r
解:长方形花坛的面积为√140×35
70π(m2).因为长方形花坛与圆形花坛的面积
相等,所以x2=70π.所以圆形花坛的半径r
70(
超越自我
比较前后两个算式计算结果的大小.(填
或
(1)2+
2×2×
(2)3+3
2×√3×√3;
(3)9+16
2×√9×√16;
通过观察与归纳,写出其中的规律,并说明
理由
解:(1)>(2)=(3)
规律:a+b≥2a·b(a≥0,b≥0)
理由:∵a=(a)2,b=(b)2(a≥0,b≥0)
a+b-2a·√b=(a)2-2a·√b+(b)
a+b≥2√a·√b(a≥0,b≥0)
