【华师大版】数学九年级上册 21.3 二次根式的加减 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 21.3 二次根式的加减 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:10:06 | ||
图片预览








文档简介
(共22张PPT)
课前预习
领习新知
几个二次根式化为最简二次根式以后,如果
被开方数相同,那么这几个二次根式就叫
做同类二次根式
2.二次根式的加减运算,先化简每一个二次根
式,然后合并同类二次根式
并同类二次根式的方法,是将同类二次根式
前面的数或式子相加减,根指数和被开
方数都不变
4
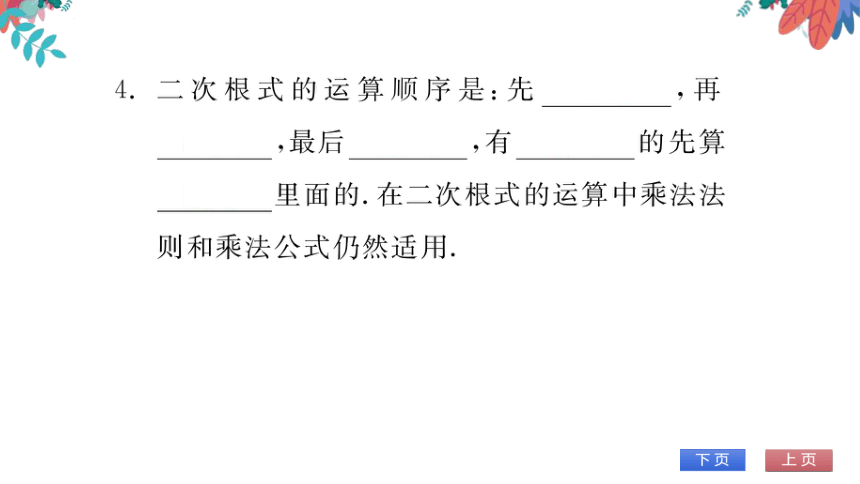
次根式的运算顺序是:先乘方,再
乘除,最后加减,有括号的先算
括号里面的.在二次根式的运算中乘法法
则和乘法公式仍然适用
当堂训练
巩固基础
知识点1同类二次根式
1.下列二次根式中,能与3合并的是
( B
C.√24D.√0.3
2.下列二次根式中,属于同类二次根式的是
A.2√3与√6
B.
C.√18与
D.√4a与√8a
知识点2二次根式的加减
(营口)化简√27+√3
2的结果是(D
A.0
C.-2√3D.2√3
4.下列计算中,错误的是
3b=√3(a-b)
B.52a+22a=7√2
C.5√ab-6b
b
D.4x-√x=3x√x
计算:
(1)√80
20
解:原式=45-25+5
(2)
27
解:原式=3+3
(3)(48—4
4√0.5
3
4
解:原式=(43-53
3
4
4
4
+2√2
√3+2√2
知识点3二次根式的混合运算
7.计算:(√2+1)(2-1)=1
8.计算:
(1)(5+2)
解:原式=9+45
(2)(23-2)2
解:原式=14-46
课后作业
全面提升
下列各数中,与2-√3的积为有理数的是
A.2
B.2-3
若a,b为有理数,且4+√8
8
则ab的值为
13
13
B
D.2
3.若√3的整数部分为a,小数部分为b,则3a
4.计算
(1)312-3/11
48-√27
(2)√32+√0.5
13
解:原式=42+2
1814
√2+5
N
+3
(3)8x
15
4
解:原式=4xx-x-5xx+xx
计算:
(1)(√2-√3)
解:原式=2-26+3+6
4
(2)
√48)÷2√3
解:原式
4
10√3×
14
6.已知x=√2-1,y=√2+1,求2xy+y2
的值
解:
2 cv
超越自我
7.已知
5),求下
列各式的值:
(1)x
(2)
解
(√7
y
(1)x2-xy+y2=(x+y)2-3xy=(7)2
3
2
)2-2x
(2)
y
y
课前预习
领习新知
几个二次根式化为最简二次根式以后,如果
被开方数相同,那么这几个二次根式就叫
做同类二次根式
2.二次根式的加减运算,先化简每一个二次根
式,然后合并同类二次根式
并同类二次根式的方法,是将同类二次根式
前面的数或式子相加减,根指数和被开
方数都不变
4
次根式的运算顺序是:先乘方,再
乘除,最后加减,有括号的先算
括号里面的.在二次根式的运算中乘法法
则和乘法公式仍然适用
当堂训练
巩固基础
知识点1同类二次根式
1.下列二次根式中,能与3合并的是
( B
C.√24D.√0.3
2.下列二次根式中,属于同类二次根式的是
A.2√3与√6
B.
C.√18与
D.√4a与√8a
知识点2二次根式的加减
(营口)化简√27+√3
2的结果是(D
A.0
C.-2√3D.2√3
4.下列计算中,错误的是
3b=√3(a-b)
B.52a+22a=7√2
C.5√ab-6b
b
D.4x-√x=3x√x
计算:
(1)√80
20
解:原式=45-25+5
(2)
27
解:原式=3+3
(3)(48—4
4√0.5
3
4
解:原式=(43-53
3
4
4
4
+2√2
√3+2√2
知识点3二次根式的混合运算
7.计算:(√2+1)(2-1)=1
8.计算:
(1)(5+2)
解:原式=9+45
(2)(23-2)2
解:原式=14-46
课后作业
全面提升
下列各数中,与2-√3的积为有理数的是
A.2
B.2-3
若a,b为有理数,且4+√8
8
则ab的值为
13
13
B
D.2
3.若√3的整数部分为a,小数部分为b,则3a
4.计算
(1)312-3/11
48-√27
(2)√32+√0.5
13
解:原式=42+2
1814
√2+5
N
+3
(3)8x
15
4
解:原式=4xx-x-5xx+xx
计算:
(1)(√2-√3)
解:原式=2-26+3+6
4
(2)
√48)÷2√3
解:原式
4
10√3×
14
6.已知x=√2-1,y=√2+1,求2xy+y2
的值
解:
2 cv
超越自我
7.已知
5),求下
列各式的值:
(1)x
(2)
解
(√7
y
(1)x2-xy+y2=(x+y)2-3xy=(7)2
3
2
)2-2x
(2)
y
y
