【华师大版】数学九年级上册 22.2.3 公式法 习题课件
文档属性
| 名称 | 【华师大版】数学九年级上册 22.2.3 公式法 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:11:55 | ||
图片预览








文档简介
(共25张PPT)
课前预习
预习新知
1.一元二次方程ax2+bx+c=0(a≠0)的求根公
6+vb2-4ac
式是x
2a
,用公式法解一元
二次方程必须满足的条件是b-4ac≥0
在方程4x2+4x+1=0中,b-4ac的值为0
3.用公式法解一元二次方程的一般步骤:
(1)把一元二次方程化为一般形式
(2)确定a,b,c的值
3)计算b2-4ac的值;
4)当b2-4aC≥0时,把a,b,c的值代入求根公
式,求得方程的两个实数根(当b2-4ac<
时,方程无实数根)
堂训练
巩固基础
知识点1-元二次方程的求根公式
用公式法解方程3x2+4=12x,下列代入公式
正确的是
12±√122-3×4
12士√122×3×4
B. x
2×3
2士√12+3×4
(-12)±√(-12)2-4×3×4
D
2×3
在方程2x2-3x-3=0中,a
2,b
b2-4
3+
4
4
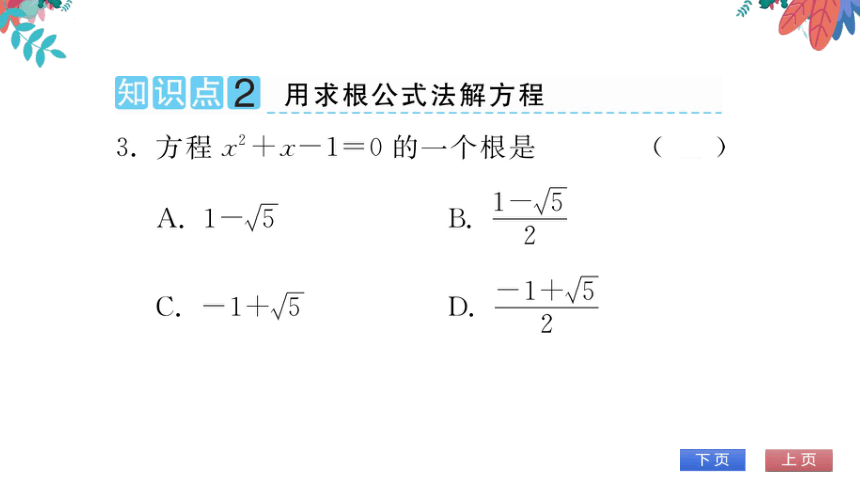
知识点2用求根公式法解方程
方程x2+x-1=0的一个根是
D
A.1
B.
D
用公式法解方程:
(1)2x2-3x+1=0;
解:x
(-3)±√(-3)2-4×2×1
2×2
(2)1-x=3x
解:3x2+x-1=0
1+√12-4×3×(-1)
2×3
1+√13
知识点3用适当的方法解一元二次方程
6.方程(x+2)2=9的最适当的解法是
A.直接开平方法B.配方法
C.公式法
D.因式分解法
用适当的方法解下列一元二次方程
(1)(x+3)2-169=0
解:(x+3)2=169,
x+3=±13,
10,x2
16
(2)(2x+3)2=4(2x+3
解:移项,得(2x+3)2-4(2x+3)=0
分解因式,得(2x+3)[(2x+3)-4]=0
2x+3=0,2x+3-4=0
(3)2
3x-1=0
解:b2-4ac=9+8=17,
3+17
2×2
3+√17
(攀枝花)若x=-2是关于x的一元二次方程
ax-a2=0的一个根,则a的值为
A.-1或4
B
或-4
C.1或-4
D.1或4
若在实数范围内定义一种运算“兴”,使a兴b
(a+1)2-ab,则方程(x+2)兴5=0的根为
2
5
3.(易错题)若两个最简二次根式√x2+3x与
x+15可以合并,则x
4.用公式法解下列方程:
(1)3y(y-3)=2(y+1)(y-1)
5.设a,b,c都是实数,且满足(2—a)
a2+b+c+c+8=0,请你求出方程ax2
bx+c=0的根
解
1+5,x
课前预习
预习新知
1.一元二次方程ax2+bx+c=0(a≠0)的求根公
6+vb2-4ac
式是x
2a
,用公式法解一元
二次方程必须满足的条件是b-4ac≥0
在方程4x2+4x+1=0中,b-4ac的值为0
3.用公式法解一元二次方程的一般步骤:
(1)把一元二次方程化为一般形式
(2)确定a,b,c的值
3)计算b2-4ac的值;
4)当b2-4aC≥0时,把a,b,c的值代入求根公
式,求得方程的两个实数根(当b2-4ac<
时,方程无实数根)
堂训练
巩固基础
知识点1-元二次方程的求根公式
用公式法解方程3x2+4=12x,下列代入公式
正确的是
12±√122-3×4
12士√122×3×4
B. x
2×3
2士√12+3×4
(-12)±√(-12)2-4×3×4
D
2×3
在方程2x2-3x-3=0中,a
2,b
b2-4
3+
4
4
知识点2用求根公式法解方程
方程x2+x-1=0的一个根是
D
A.1
B.
D
用公式法解方程:
(1)2x2-3x+1=0;
解:x
(-3)±√(-3)2-4×2×1
2×2
(2)1-x=3x
解:3x2+x-1=0
1+√12-4×3×(-1)
2×3
1+√13
知识点3用适当的方法解一元二次方程
6.方程(x+2)2=9的最适当的解法是
A.直接开平方法B.配方法
C.公式法
D.因式分解法
用适当的方法解下列一元二次方程
(1)(x+3)2-169=0
解:(x+3)2=169,
x+3=±13,
10,x2
16
(2)(2x+3)2=4(2x+3
解:移项,得(2x+3)2-4(2x+3)=0
分解因式,得(2x+3)[(2x+3)-4]=0
2x+3=0,2x+3-4=0
(3)2
3x-1=0
解:b2-4ac=9+8=17,
3+17
2×2
3+√17
(攀枝花)若x=-2是关于x的一元二次方程
ax-a2=0的一个根,则a的值为
A.-1或4
B
或-4
C.1或-4
D.1或4
若在实数范围内定义一种运算“兴”,使a兴b
(a+1)2-ab,则方程(x+2)兴5=0的根为
2
5
3.(易错题)若两个最简二次根式√x2+3x与
x+15可以合并,则x
4.用公式法解下列方程:
(1)3y(y-3)=2(y+1)(y-1)
5.设a,b,c都是实数,且满足(2—a)
a2+b+c+c+8=0,请你求出方程ax2
bx+c=0的根
解
1+5,x
