人教版小学数学五年级上册第六单元测试卷(含答案)
文档属性
| 名称 | 人教版小学数学五年级上册第六单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 231.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 14:03:04 | ||
图片预览



文档简介
第六单元测试卷
总分:100分;考试时间:90分钟;
题号 一 二 三 四 五 六 总分
得分
一、填空题(共20分)
1.(本题2分)一块三角形土地的面积是160m2,底是32m,高是(________)m。
2.(本题2分)一个平行四边形的底是13分米,高是70厘米,面积是(______)平方分米。
3.(本题2分)一个等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(___________)。
4.(本题2分)如图,直角梯形的周长,它的面积是(________)。
5.(本题2分)一个直角梯形,如果把下底减少3cm,这个梯形就变成一个边长7cm的正方形.这个梯形的面积是(_________).
6.(本题2分)如图所示,阴影部分的面积约是(_____)cm2.(每个小方格的面积为lcm2)
7.(本题6分)一个三角形的面积是56平方米,与它等底等高的平行四边形面积是________,这个三角形的面积是平行四边形面积的________,这个平行四边形面积是三角形面积的________。
8.(本题2分)如图,把一个梯形分成一个平行四边形和一个三角形,梯形的面积是32cm2,三角形的面积是(________)。
二、判断题(共10分)
9.(本题2分)一个直角三角形的三条边分别是6厘米,8厘米和10厘米,那么这个三角形的面积是24平方厘米.(______)
10.(本题2分)图中的长方形中的甲与乙两个三角形比较,甲比乙大.(____)
11.(本题2分)一个平行四边形的底是5厘米,高是底的2倍,它的面积是50平方厘米. (____)
12.(本题2分)三角形的高不变,面积要扩大到原来的10倍,必须把底扩大到原来的10倍。(________)
13.(本题2分)两个等底等高的三角形,面积相等,形状也一定完全相同。(______)
三、选择题(共10分)
14.(本题2分)下面能用5a+5b表示的是( )。
A.线段的总长度: B.平行四边形的面积:
C.梯形的面积: D.组合图形的面积:
15.(本题2分)如图,长方形的长是10厘米,宽是6厘米。将这个长方形沿对角线剪开,然后拼成一个大三角形。这个大三角形的面积是( )平方厘米。
A.60 B.32 C.30 D.16
16.(本题2分)小明把一枚银杏树叶的轮廓描在方格纸上,如下图(图中每个小方格的面积是1cm2)。这枚树叶的面积最接近( )cm2。
A.19 B.32 C.45 D.54
17.(本题2分)下图是五个同样的正方形,比较阴影部分的3个三角形的面积。( )
①>②>③ B.①<②<③ C.①=②=③ D.②>①>③
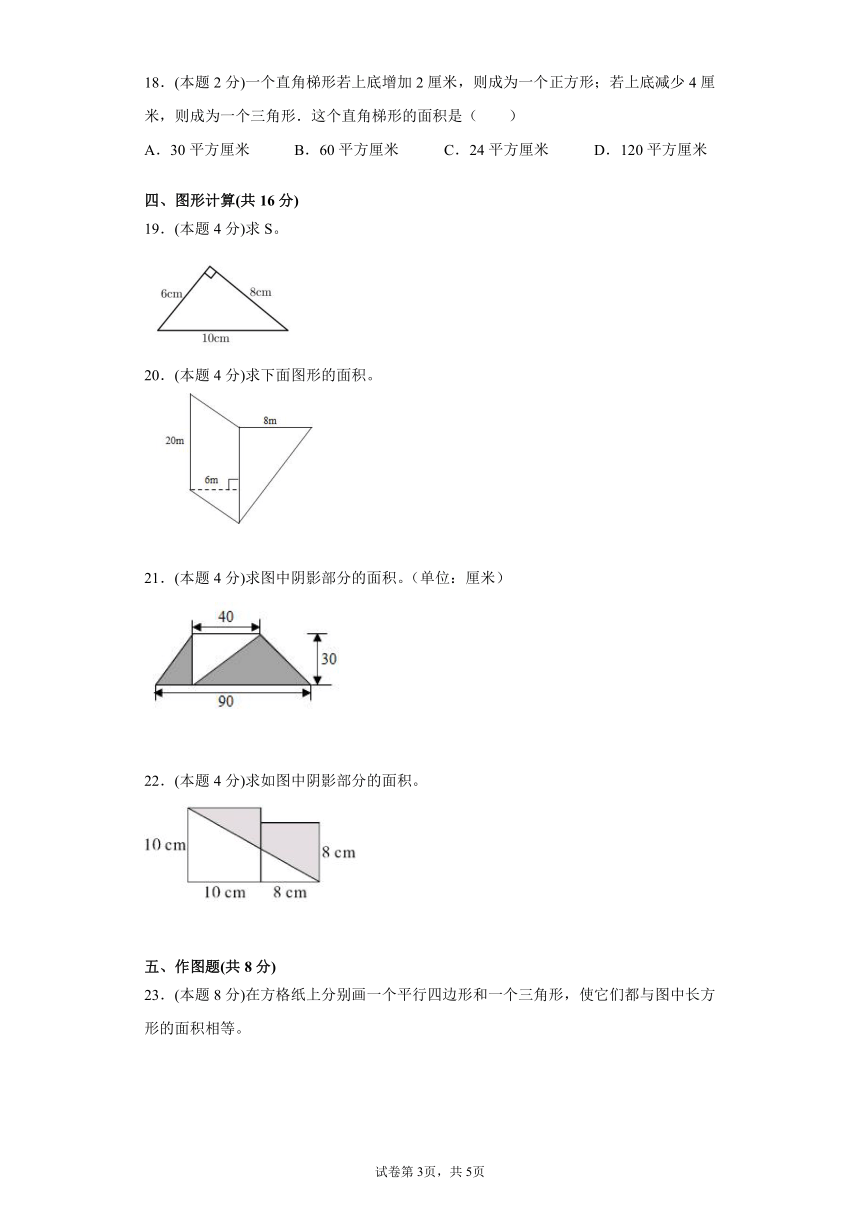
18.(本题2分)一个直角梯形若上底增加2厘米,则成为一个正方形;若上底减少4厘米,则成为一个三角形.这个直角梯形的面积是( )
A.30平方厘米 B.60平方厘米 C.24平方厘米 D.120平方厘米
四、图形计算(共16分)
19.(本题4分)求S。
20.(本题4分)求下面图形的面积。
21.(本题4分)求图中阴影部分的面积。(单位:厘米)
22.(本题4分)求如图中阴影部分的面积。
五、作图题(共8分)
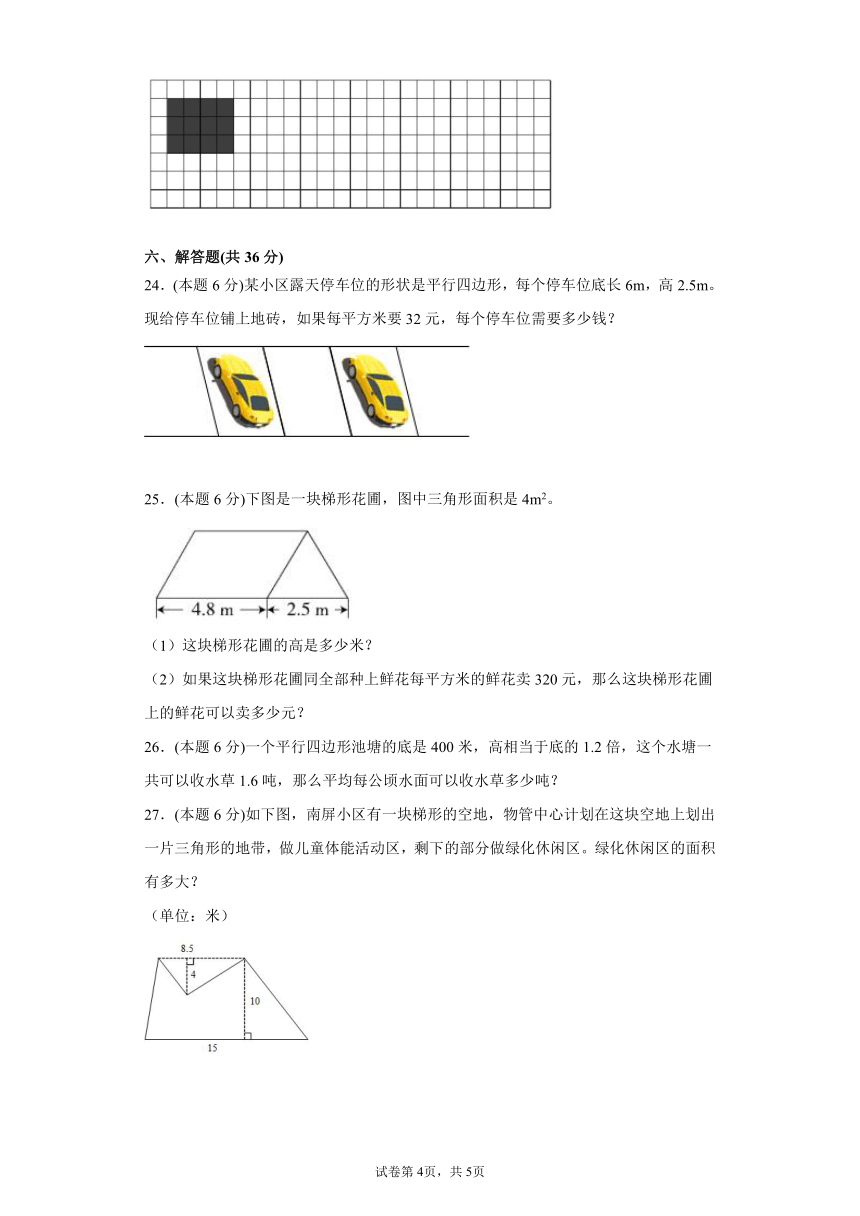
23.(本题8分)在方格纸上分别画一个平行四边形和一个三角形,使它们都与图中长方形的面积相等。
六、解答题(共36分)
24.(本题6分)某小区露天停车位的形状是平行四边形,每个停车位底长6m,高2.5m。现给停车位铺上地砖,如果每平方米要32元,每个停车位需要多少钱?
25.(本题6分)下图是一块梯形花圃,图中三角形面积是4m2。
(1)这块梯形花圃的高是多少米?
(2)如果这块梯形花圃同全部种上鲜花每平方米的鲜花卖320元,那么这块梯形花圃上的鲜花可以卖多少元?
26.(本题6分)一个平行四边形池塘的底是400米,高相当于底的1.2倍,这个水塘一共可以收水草1.6吨,那么平均每公顷水面可以收水草多少吨?
27.(本题6分)如下图,南屏小区有一块梯形的空地,物管中心计划在这块空地上划出一片三角形的地带,做儿童体能活动区,剩下的部分做绿化休闲区。绿化休闲区的面积有多大?
(单位:米)
28.(本题6分)王大伯家有一块长15米,宽8米的长方形菜地,一条底为0.8米的平行四边形道路从中穿过,把这块菜地分成了一个三角形和一个梯形。
(1)请你在图中画出小路的位置和形状。
(2)求出你所画的小路的面积。
29.(本题6分)下面是一面墙,中间有一扇长2m、宽1.5m的窗户。如果每平方米用砖180块,砌这面墙一共用多少块砖?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.10
【分析】
根据“三角形的高=面积×2÷底”解答即可。
【详解】
160×2÷32
=320÷32
=10(米)
【点睛】
熟练掌握三角形的面积公式并能灵活利用是解答本题的关键。
2.91
【分析】
根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【详解】
70厘米=7分米,
13×7=91(平方分米)
【点睛】
此题需要考查平行四边形面积公式的灵活运用,关键是熟记公式。
3.12厘米
【详解】
略
4.88
【分析】
用40去掉两条腰,得上下底的和,再利用梯形面积公式即可求得解。据此解答。
【详解】
40-(10+8)
=40-18
=22(厘米)
22×8÷2
=176÷2
=88(平方厘米)
【点睛】
本题虽然求不出上底和下底的具体长度,但是利用上下底的和的数值乘高除以2,是解答此题的关键。
5.59.5cm
【详解】
略
6.30
【详解】
如图:
6×5=30(平方厘米)
答:阴影部分面积大约是30平方厘米.
故答案为30.
7.112平方米 一半 2倍
【解析】
【分析】
平行四边形面积=底×高,三角形面积=底×高÷2,所以等底等高的平行四边形面积是三角形面积的2倍。由此计算即可。
【详解】
平行四边形面积:56×2=112(平方米);三角形面积是平行四边形面积的一半,这个平行四边形面积是三角形面积的2倍。
故答案为:112平方米;一半;2倍
8.8cm2
【分析】
根据“梯形的高=面积×2÷(上底+下底)”,求出梯形的高,再根据“三角形的面积=底×高÷2”进行解答即可。
【详解】
32×2÷(6+10)
=64÷16
=4(厘米);
(10-6)×4÷2
=4×4÷2
=8(平方厘米)
【点睛】
求出梯形的高是解答本题的关键。
9.√
【详解】
8×6÷2=24(cm ),原题计算正确.
10.错误
【分析】
等底等高的三角形面积相等,把甲、乙每个图形的面积都看作两个三角形的面积之差,这样就能确定甲乙的大小关系.
【详解】
因为三角形ADE和三角形BDE等底等高,所以三角形ADE和三角形BDE面积相等,三角形ADE﹣三角形DOE的面积=三角形BDE面积﹣三角形DOE的面积,所以甲和乙的面积相等;原题说法错误.
故答案为错误
11.正确
【详解】
略
12.√
【分析】
三角形的高不变,底扩大到原来的多少倍,面积就会扩大到原来的多少倍,据此解答即可。
【详解】
三角形的高不变,面积要扩大到原来的10倍,则必须把底扩大到原来的10倍,原题说法正确;
故答案为:√。
【点睛】
熟记三角形的面积公式并能灵活利用是解答本题的关键。
13.×
【分析】
三角形面积=底×高÷2,等底等高的三角形多种多样,据此分析。
【详解】
如图,三个三角形等底等高,面积相同,形状不同,所以原题说法错误。
【点睛】
关键是熟悉三角形特征,掌握三角形面积公式。
14.D
【分析】
逐一分析每个选项,最后判断即可。
【详解】
A.线段总长度为5+a+b,不符合;
B.平行四边形面积为5b,不符合;
C.梯形面积为(a+b)×5÷2,不符合;
D.组合图形的面积:5(a+b)=5a+5b,符合。
故答案为:D。
【点睛】
本题考查用字母表示数、长方形、平行四边形和梯形的面积,解答本题的关键是掌握长方形、平行四边形和梯形的面积计算公式。
15.A
【分析】
根据图形的面积的定义可知,这个长方形的面积等于这两个三角形的面积之和,将这个长方形沿对角剪开,然后拼成一个大三角形,拼成的三角形的面积也等于这两个三角形的面积之和,据此即可选择。
【详解】
10×6=60(平方厘米)
故答案为:A。
【点睛】
此题考查图形的拼组以及长方形的面积的计算方法。
16.B
【分析】
将不规则的银杏树叶的面积,用一个长方形来近似。然后数出长方形的面积,选出选项中最接近的面积即可。
长方形近似图,如下:
【详解】
长方形的面积为36cm2,结合各选项,与36cm2最接近的是32cm2。
故答案为:B
【点睛】
本题考查了不规则图形面积,求不规则图形的面积,常用规则图形的面积来近似。
17.C
【分析】
三角形的面积公式S=ah÷2,3个三角形的底和高都是正方形的边长,3个三角形是等底等高,所以它们的面积相等。
【详解】
阴影部分的3个三角形的面积相等即①=②=③。
故选:C。
【点睛】
掌握:“等底等高的三角形面积相等”是解题的关键。
18.A
【分析】
如图所示,由“直角梯形若上底增加2厘米,则成为一个正方形;若上底减少4厘米,则成为一个三角形,可得:平行四边形的上底为4厘米,下底为(4+2)厘米,高为(4+2)厘米,可以利用梯形的面积公式求解.
【详解】
梯形的面积为:(4+4+2)×(4+2)÷2,
=10×6÷2,
=60÷2,
=30(平方厘米);
答:这个直角梯形的面积是30平方厘米.
故选A.
19.24平方厘米
【分析】
看图可知,这个三角形的底和高分别为6厘米、8厘米,据此利用三角形的面积公式列式计算出它的面积即可。
【详解】
6×8÷2=24(平方厘米)
20.200平方米
【分析】
组合图形的面积=平行四边形的面积+三角形的面积
【详解】
20×6+20×8÷2
=120+80
=200(平方米)
21.1350平方厘米
【分析】
阴影部分的面积=梯形的面积-空白部分三角形的面积。
【详解】
(90+40)×30÷2-40×30÷2
=130×30÷2-40×30÷2
=3900÷2-1200÷2
=1950-600
=1350(平方厘米)
所以,阴影部分面积是1350平方厘米。
22.74cm2
【分析】
由图意可知,阴影部分的面积等于两个正方形的面积之和减去一个底为(10+8)cm、高为10cm的三角形的面积;正方形的面积=边长×边长,三角形的面积=底×高÷2,据此解答。
【详解】
10×10+8×8-(10+8)×10÷2
=100+64-18×10÷2
=164-90
=74(cm2)
23.见详解
【分析】
假设小正方形边长为1,图中长方形的长是4,宽是3,面积是4×3=12;
当平行四边形的面积为12时,平行四边形的底为6,高为2,面积是6×2=12;
当三角形的面积为12时,三角形的底为6,高为4,面积是6×4÷2=12,据此作图。
【详解】
【点睛】
根据长方形的面积计算出平行四边形和三角形的底和高是解答题目的关键。
24.480元
【分析】
用6×2.5求出每个停车位的面积,再乘每平方米需要的钱数即可。
【详解】
6×2.5×32
=15×32
=480(元);
答:每个停车位需要480元。
【点睛】
熟练掌握平行四边形的面积是解答本题的关键。
25.(1)3.2m
(2)6195.2元
【分析】
(1)由图知:三角形的高就是梯形的高。三角形面积是4平方米,用4乘2除以底2.5,得三角形高。即而得梯形高。
(2)梯形的上底是4.8米,下底是4.8+2.5=7.3米,高已求得,用梯形面积公式求得梯形花圃的面积,进而求得卖的鲜花总价。
【详解】
(1)4×2÷2.5
=8÷2.5
=3.2(米)
答:这块梯形花圃的高是3.2米。
(2)[4.8+(4.8+2.5)]×3.2÷2×320
=[4.8+7.3]×3.2÷2×320
=12.1×3.2÷2×320
=38.72÷2×320
=19.36×320
=6195.2(元)
答:这块梯形花圃上的鲜花可以卖6195.2元。
【点睛】
认识到三角形的高就是梯形的高,进而求得梯形的面积是解答本题的关键。
26.0.083吨
【分析】
用400×1.2求出平行四边形的高,再根据“平行四边形的面积=底×高”求出平行四边形的面积,再用总吨数除以面积即可。
【详解】
400×1.2×400
=480×400
=192000(平方米);
192000平方米=19.2公顷;
1.6÷19.2≈0.083(吨);
答:平均每公顷水面可以收水草0.083吨。
【点睛】
熟练掌握平行四边形的面积公式是解答本题的关键。
27.100.5平方米
【分析】
根据图意可知,绿化休闲区的面积=梯形面积-三角形面积,代入数据求解。
【详解】
(8.5+15)×10÷2-8.5×4÷2
=23.5×10÷2-34÷2
=117.5-17
=100.5(平方米)
答:绿化休闲区的面积为100.5平方米。
【点睛】
此题考查的是梯形面积和三角形面积公式的应用,熟记公式是解题关键。
28.(1)见详解
(2)12平方米或6.4平方米
【分析】
(1)平行四边形:对边平行且相等,没有对称轴,长方形的长可以做平行四边行的高;长方形的宽也可以做平行四边形的高,据此分两种情况画出示意图;
(2)根据平行四边形的面积=底×高,求出面积即可。
【详解】
(1)
(2)(平方米)或(平方米)
答:小路的面积是12平方米或6.4平方米。
【点睛】
关键是熟悉平行四边形的特征,掌握平行四边形面积公式。
29.3690块
【分析】
需要用砖部分的面积=三角形的面积+长方形的面积-窗户的面积,需要用砖的总块数=每平方米用砖的块数×需要用砖部分的面积,据此解答。
【详解】
=3690(块)
答:砌这面墙一共用3690块砖。
【点睛】
熟练运用面积公式求出需要用砖部分的总面积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
总分:100分;考试时间:90分钟;
题号 一 二 三 四 五 六 总分
得分
一、填空题(共20分)
1.(本题2分)一块三角形土地的面积是160m2,底是32m,高是(________)m。
2.(本题2分)一个平行四边形的底是13分米,高是70厘米,面积是(______)平方分米。
3.(本题2分)一个等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(___________)。
4.(本题2分)如图,直角梯形的周长,它的面积是(________)。
5.(本题2分)一个直角梯形,如果把下底减少3cm,这个梯形就变成一个边长7cm的正方形.这个梯形的面积是(_________).
6.(本题2分)如图所示,阴影部分的面积约是(_____)cm2.(每个小方格的面积为lcm2)
7.(本题6分)一个三角形的面积是56平方米,与它等底等高的平行四边形面积是________,这个三角形的面积是平行四边形面积的________,这个平行四边形面积是三角形面积的________。
8.(本题2分)如图,把一个梯形分成一个平行四边形和一个三角形,梯形的面积是32cm2,三角形的面积是(________)。
二、判断题(共10分)
9.(本题2分)一个直角三角形的三条边分别是6厘米,8厘米和10厘米,那么这个三角形的面积是24平方厘米.(______)
10.(本题2分)图中的长方形中的甲与乙两个三角形比较,甲比乙大.(____)
11.(本题2分)一个平行四边形的底是5厘米,高是底的2倍,它的面积是50平方厘米. (____)
12.(本题2分)三角形的高不变,面积要扩大到原来的10倍,必须把底扩大到原来的10倍。(________)
13.(本题2分)两个等底等高的三角形,面积相等,形状也一定完全相同。(______)
三、选择题(共10分)
14.(本题2分)下面能用5a+5b表示的是( )。
A.线段的总长度: B.平行四边形的面积:
C.梯形的面积: D.组合图形的面积:
15.(本题2分)如图,长方形的长是10厘米,宽是6厘米。将这个长方形沿对角线剪开,然后拼成一个大三角形。这个大三角形的面积是( )平方厘米。
A.60 B.32 C.30 D.16
16.(本题2分)小明把一枚银杏树叶的轮廓描在方格纸上,如下图(图中每个小方格的面积是1cm2)。这枚树叶的面积最接近( )cm2。
A.19 B.32 C.45 D.54
17.(本题2分)下图是五个同样的正方形,比较阴影部分的3个三角形的面积。( )
①>②>③ B.①<②<③ C.①=②=③ D.②>①>③
18.(本题2分)一个直角梯形若上底增加2厘米,则成为一个正方形;若上底减少4厘米,则成为一个三角形.这个直角梯形的面积是( )
A.30平方厘米 B.60平方厘米 C.24平方厘米 D.120平方厘米
四、图形计算(共16分)
19.(本题4分)求S。
20.(本题4分)求下面图形的面积。
21.(本题4分)求图中阴影部分的面积。(单位:厘米)
22.(本题4分)求如图中阴影部分的面积。
五、作图题(共8分)
23.(本题8分)在方格纸上分别画一个平行四边形和一个三角形,使它们都与图中长方形的面积相等。
六、解答题(共36分)
24.(本题6分)某小区露天停车位的形状是平行四边形,每个停车位底长6m,高2.5m。现给停车位铺上地砖,如果每平方米要32元,每个停车位需要多少钱?
25.(本题6分)下图是一块梯形花圃,图中三角形面积是4m2。
(1)这块梯形花圃的高是多少米?
(2)如果这块梯形花圃同全部种上鲜花每平方米的鲜花卖320元,那么这块梯形花圃上的鲜花可以卖多少元?
26.(本题6分)一个平行四边形池塘的底是400米,高相当于底的1.2倍,这个水塘一共可以收水草1.6吨,那么平均每公顷水面可以收水草多少吨?
27.(本题6分)如下图,南屏小区有一块梯形的空地,物管中心计划在这块空地上划出一片三角形的地带,做儿童体能活动区,剩下的部分做绿化休闲区。绿化休闲区的面积有多大?
(单位:米)
28.(本题6分)王大伯家有一块长15米,宽8米的长方形菜地,一条底为0.8米的平行四边形道路从中穿过,把这块菜地分成了一个三角形和一个梯形。
(1)请你在图中画出小路的位置和形状。
(2)求出你所画的小路的面积。
29.(本题6分)下面是一面墙,中间有一扇长2m、宽1.5m的窗户。如果每平方米用砖180块,砌这面墙一共用多少块砖?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.10
【分析】
根据“三角形的高=面积×2÷底”解答即可。
【详解】
160×2÷32
=320÷32
=10(米)
【点睛】
熟练掌握三角形的面积公式并能灵活利用是解答本题的关键。
2.91
【分析】
根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【详解】
70厘米=7分米,
13×7=91(平方分米)
【点睛】
此题需要考查平行四边形面积公式的灵活运用,关键是熟记公式。
3.12厘米
【详解】
略
4.88
【分析】
用40去掉两条腰,得上下底的和,再利用梯形面积公式即可求得解。据此解答。
【详解】
40-(10+8)
=40-18
=22(厘米)
22×8÷2
=176÷2
=88(平方厘米)
【点睛】
本题虽然求不出上底和下底的具体长度,但是利用上下底的和的数值乘高除以2,是解答此题的关键。
5.59.5cm
【详解】
略
6.30
【详解】
如图:
6×5=30(平方厘米)
答:阴影部分面积大约是30平方厘米.
故答案为30.
7.112平方米 一半 2倍
【解析】
【分析】
平行四边形面积=底×高,三角形面积=底×高÷2,所以等底等高的平行四边形面积是三角形面积的2倍。由此计算即可。
【详解】
平行四边形面积:56×2=112(平方米);三角形面积是平行四边形面积的一半,这个平行四边形面积是三角形面积的2倍。
故答案为:112平方米;一半;2倍
8.8cm2
【分析】
根据“梯形的高=面积×2÷(上底+下底)”,求出梯形的高,再根据“三角形的面积=底×高÷2”进行解答即可。
【详解】
32×2÷(6+10)
=64÷16
=4(厘米);
(10-6)×4÷2
=4×4÷2
=8(平方厘米)
【点睛】
求出梯形的高是解答本题的关键。
9.√
【详解】
8×6÷2=24(cm ),原题计算正确.
10.错误
【分析】
等底等高的三角形面积相等,把甲、乙每个图形的面积都看作两个三角形的面积之差,这样就能确定甲乙的大小关系.
【详解】
因为三角形ADE和三角形BDE等底等高,所以三角形ADE和三角形BDE面积相等,三角形ADE﹣三角形DOE的面积=三角形BDE面积﹣三角形DOE的面积,所以甲和乙的面积相等;原题说法错误.
故答案为错误
11.正确
【详解】
略
12.√
【分析】
三角形的高不变,底扩大到原来的多少倍,面积就会扩大到原来的多少倍,据此解答即可。
【详解】
三角形的高不变,面积要扩大到原来的10倍,则必须把底扩大到原来的10倍,原题说法正确;
故答案为:√。
【点睛】
熟记三角形的面积公式并能灵活利用是解答本题的关键。
13.×
【分析】
三角形面积=底×高÷2,等底等高的三角形多种多样,据此分析。
【详解】
如图,三个三角形等底等高,面积相同,形状不同,所以原题说法错误。
【点睛】
关键是熟悉三角形特征,掌握三角形面积公式。
14.D
【分析】
逐一分析每个选项,最后判断即可。
【详解】
A.线段总长度为5+a+b,不符合;
B.平行四边形面积为5b,不符合;
C.梯形面积为(a+b)×5÷2,不符合;
D.组合图形的面积:5(a+b)=5a+5b,符合。
故答案为:D。
【点睛】
本题考查用字母表示数、长方形、平行四边形和梯形的面积,解答本题的关键是掌握长方形、平行四边形和梯形的面积计算公式。
15.A
【分析】
根据图形的面积的定义可知,这个长方形的面积等于这两个三角形的面积之和,将这个长方形沿对角剪开,然后拼成一个大三角形,拼成的三角形的面积也等于这两个三角形的面积之和,据此即可选择。
【详解】
10×6=60(平方厘米)
故答案为:A。
【点睛】
此题考查图形的拼组以及长方形的面积的计算方法。
16.B
【分析】
将不规则的银杏树叶的面积,用一个长方形来近似。然后数出长方形的面积,选出选项中最接近的面积即可。
长方形近似图,如下:
【详解】
长方形的面积为36cm2,结合各选项,与36cm2最接近的是32cm2。
故答案为:B
【点睛】
本题考查了不规则图形面积,求不规则图形的面积,常用规则图形的面积来近似。
17.C
【分析】
三角形的面积公式S=ah÷2,3个三角形的底和高都是正方形的边长,3个三角形是等底等高,所以它们的面积相等。
【详解】
阴影部分的3个三角形的面积相等即①=②=③。
故选:C。
【点睛】
掌握:“等底等高的三角形面积相等”是解题的关键。
18.A
【分析】
如图所示,由“直角梯形若上底增加2厘米,则成为一个正方形;若上底减少4厘米,则成为一个三角形,可得:平行四边形的上底为4厘米,下底为(4+2)厘米,高为(4+2)厘米,可以利用梯形的面积公式求解.
【详解】
梯形的面积为:(4+4+2)×(4+2)÷2,
=10×6÷2,
=60÷2,
=30(平方厘米);
答:这个直角梯形的面积是30平方厘米.
故选A.
19.24平方厘米
【分析】
看图可知,这个三角形的底和高分别为6厘米、8厘米,据此利用三角形的面积公式列式计算出它的面积即可。
【详解】
6×8÷2=24(平方厘米)
20.200平方米
【分析】
组合图形的面积=平行四边形的面积+三角形的面积
【详解】
20×6+20×8÷2
=120+80
=200(平方米)
21.1350平方厘米
【分析】
阴影部分的面积=梯形的面积-空白部分三角形的面积。
【详解】
(90+40)×30÷2-40×30÷2
=130×30÷2-40×30÷2
=3900÷2-1200÷2
=1950-600
=1350(平方厘米)
所以,阴影部分面积是1350平方厘米。
22.74cm2
【分析】
由图意可知,阴影部分的面积等于两个正方形的面积之和减去一个底为(10+8)cm、高为10cm的三角形的面积;正方形的面积=边长×边长,三角形的面积=底×高÷2,据此解答。
【详解】
10×10+8×8-(10+8)×10÷2
=100+64-18×10÷2
=164-90
=74(cm2)
23.见详解
【分析】
假设小正方形边长为1,图中长方形的长是4,宽是3,面积是4×3=12;
当平行四边形的面积为12时,平行四边形的底为6,高为2,面积是6×2=12;
当三角形的面积为12时,三角形的底为6,高为4,面积是6×4÷2=12,据此作图。
【详解】
【点睛】
根据长方形的面积计算出平行四边形和三角形的底和高是解答题目的关键。
24.480元
【分析】
用6×2.5求出每个停车位的面积,再乘每平方米需要的钱数即可。
【详解】
6×2.5×32
=15×32
=480(元);
答:每个停车位需要480元。
【点睛】
熟练掌握平行四边形的面积是解答本题的关键。
25.(1)3.2m
(2)6195.2元
【分析】
(1)由图知:三角形的高就是梯形的高。三角形面积是4平方米,用4乘2除以底2.5,得三角形高。即而得梯形高。
(2)梯形的上底是4.8米,下底是4.8+2.5=7.3米,高已求得,用梯形面积公式求得梯形花圃的面积,进而求得卖的鲜花总价。
【详解】
(1)4×2÷2.5
=8÷2.5
=3.2(米)
答:这块梯形花圃的高是3.2米。
(2)[4.8+(4.8+2.5)]×3.2÷2×320
=[4.8+7.3]×3.2÷2×320
=12.1×3.2÷2×320
=38.72÷2×320
=19.36×320
=6195.2(元)
答:这块梯形花圃上的鲜花可以卖6195.2元。
【点睛】
认识到三角形的高就是梯形的高,进而求得梯形的面积是解答本题的关键。
26.0.083吨
【分析】
用400×1.2求出平行四边形的高,再根据“平行四边形的面积=底×高”求出平行四边形的面积,再用总吨数除以面积即可。
【详解】
400×1.2×400
=480×400
=192000(平方米);
192000平方米=19.2公顷;
1.6÷19.2≈0.083(吨);
答:平均每公顷水面可以收水草0.083吨。
【点睛】
熟练掌握平行四边形的面积公式是解答本题的关键。
27.100.5平方米
【分析】
根据图意可知,绿化休闲区的面积=梯形面积-三角形面积,代入数据求解。
【详解】
(8.5+15)×10÷2-8.5×4÷2
=23.5×10÷2-34÷2
=117.5-17
=100.5(平方米)
答:绿化休闲区的面积为100.5平方米。
【点睛】
此题考查的是梯形面积和三角形面积公式的应用,熟记公式是解题关键。
28.(1)见详解
(2)12平方米或6.4平方米
【分析】
(1)平行四边形:对边平行且相等,没有对称轴,长方形的长可以做平行四边行的高;长方形的宽也可以做平行四边形的高,据此分两种情况画出示意图;
(2)根据平行四边形的面积=底×高,求出面积即可。
【详解】
(1)
(2)(平方米)或(平方米)
答:小路的面积是12平方米或6.4平方米。
【点睛】
关键是熟悉平行四边形的特征,掌握平行四边形面积公式。
29.3690块
【分析】
需要用砖部分的面积=三角形的面积+长方形的面积-窗户的面积,需要用砖的总块数=每平方米用砖的块数×需要用砖部分的面积,据此解答。
【详解】
=3690(块)
答:砌这面墙一共用3690块砖。
【点睛】
熟练运用面积公式求出需要用砖部分的总面积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
