【沪科版】数学七年级上册 第1章 专题二 有理数的混合运算 习题课件
文档属性
| 名称 | 【沪科版】数学七年级上册 第1章 专题二 有理数的混合运算 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:10:06 | ||
图片预览


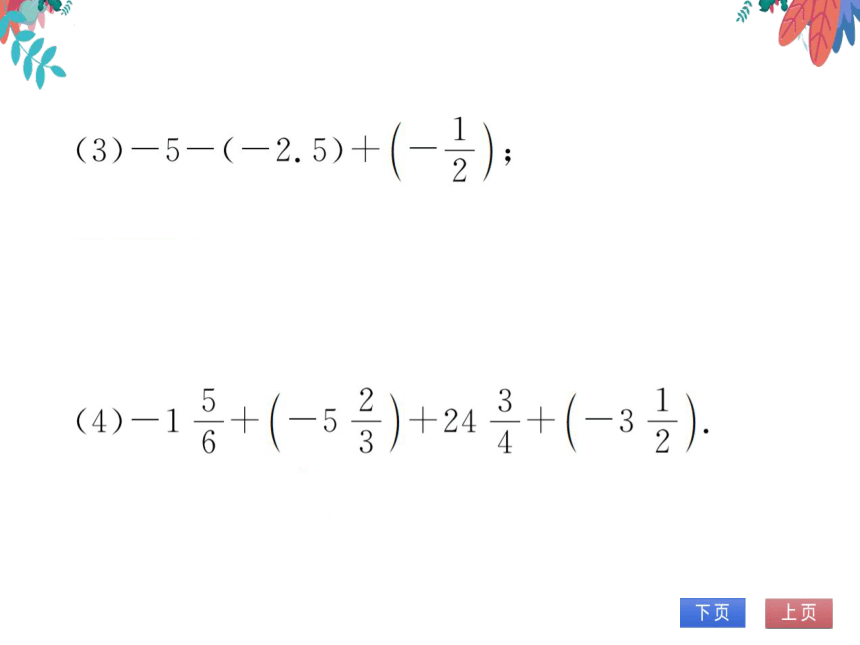

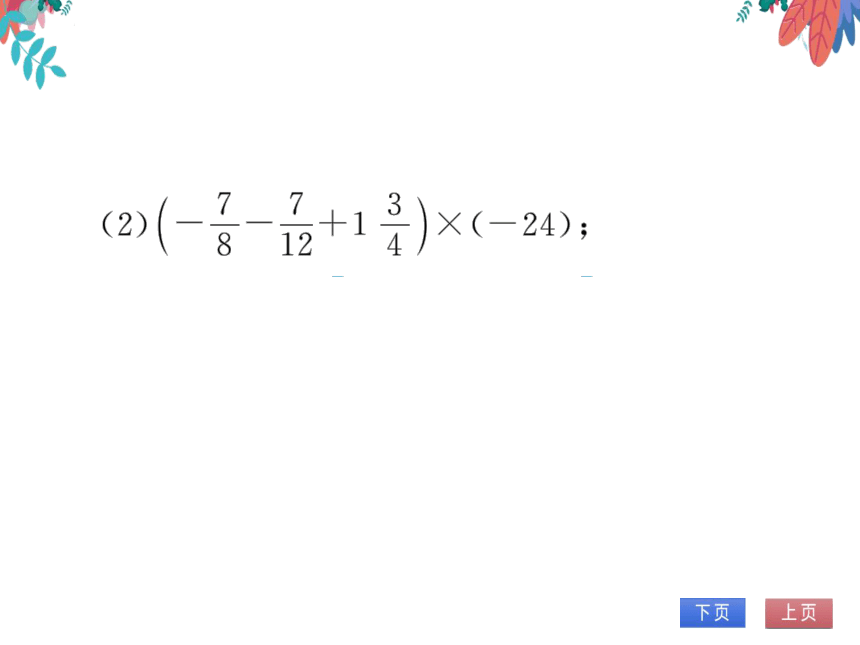


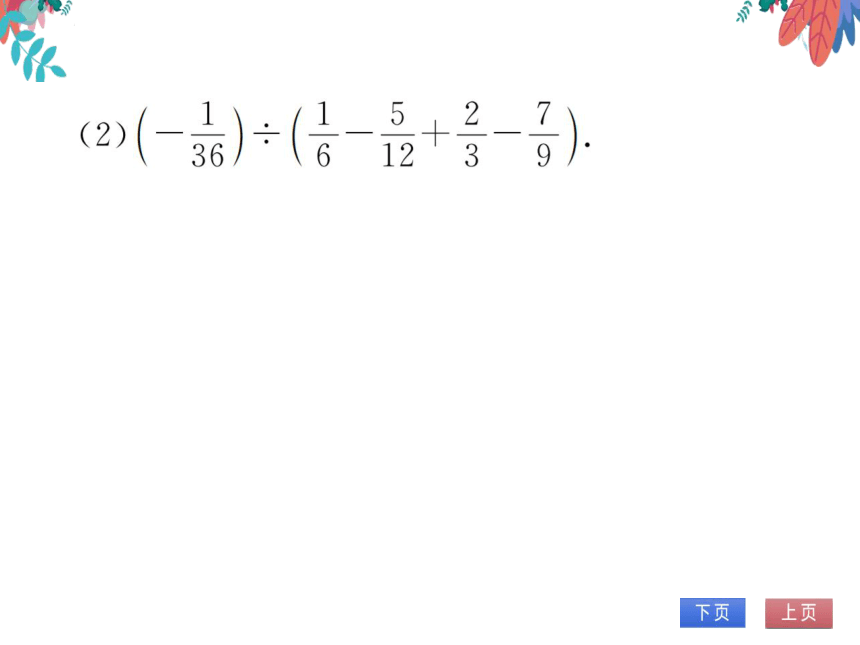

文档简介
(共28张PPT)
类型1运算律在有理数加法中的应用
计算:
(1)23-17—(-7)+(-16);
解:原式=-3
(2)(滁州)(-8)十10+2+(-1);
解:原式=3
(3)-5-(-2.5)+
解:原式
(4)-1+(-5
23
+24+(-3
4
解:原式=13°
类型2运算律在有理数混合运算中的应用
2.计算
22
22
22
(1)—7×
19
5
22
解:原式
(-7+19-5)
22
7
(2
(-24)
812
4
解:原式
(-24)
(-24)+
1×(-24)
4
21+14-42
(3)
326
解:原式
+
16
6
2+3-1
类型3利用倒数法进行计算
3.计算
30
1x6
310
解:原式的倒数为
251
1x6
12
310
30
21
(-30)
20+3-5+12
则原式
1527
(2
36
61239
解:原式的倒数为
1527
6123
36
(-36)
6+15-24+28=13,
则原式=1
13
类型4有理数的混合运算
4.计算:
4
(1)8
16
解:原式
4
(2)(-49)
742
×
(-8)
解:原式
5.计算:
(1)-14+(-2)3:4×[5—(-3)2
解:原式=7
(2)(山西)(-3-1)
解:原式=-5
(3)(阜阳)-13--3+8-4×
解:原式=-13-3+8-1
(4
)(
2)2×(-0.5)2+32÷(-3);
解:原式
22×0.25+9÷(-3)
0.5-3
(5)(-1)4-(1-0.5)3×(-2)4×[2—(—3)2]
解:原式=1-×16×(-7)
1+14
(6)-32+16÷(-2)×+(-1)2020
解:原式=-9-4+1
(7)
(-4)
12
解:原式
×13132
i
494
16
12
(8)-32:2×
3)+4-2×
1)2
解:原式
944
4949
9÷×+4-4×
9××。74~4
20
+4
16
6.简便计算:
(1)
×18-1.45×6+3.95×6
解:原式
×1Q5
×18+×18)
(-1.45+3.95)×6
(14-15+5)+2.5×6
4+15
25
16
(2)75×16
32
25
25
解:原式=(75+
32)×(16×16
25
25)、16
75+
32)×16+(75+
3225
25
1625
16
75×16+×16+75×十
253225
25
1200+=+48+
1261
类型1运算律在有理数加法中的应用
计算:
(1)23-17—(-7)+(-16);
解:原式=-3
(2)(滁州)(-8)十10+2+(-1);
解:原式=3
(3)-5-(-2.5)+
解:原式
(4)-1+(-5
23
+24+(-3
4
解:原式=13°
类型2运算律在有理数混合运算中的应用
2.计算
22
22
22
(1)—7×
19
5
22
解:原式
(-7+19-5)
22
7
(2
(-24)
812
4
解:原式
(-24)
(-24)+
1×(-24)
4
21+14-42
(3)
326
解:原式
+
16
6
2+3-1
类型3利用倒数法进行计算
3.计算
30
1x6
310
解:原式的倒数为
251
1x6
12
310
30
21
(-30)
20+3-5+12
则原式
1527
(2
36
61239
解:原式的倒数为
1527
6123
36
(-36)
6+15-24+28=13,
则原式=1
13
类型4有理数的混合运算
4.计算:
4
(1)8
16
解:原式
4
(2)(-49)
742
×
(-8)
解:原式
5.计算:
(1)-14+(-2)3:4×[5—(-3)2
解:原式=7
(2)(山西)(-3-1)
解:原式=-5
(3)(阜阳)-13--3+8-4×
解:原式=-13-3+8-1
(4
)(
2)2×(-0.5)2+32÷(-3);
解:原式
22×0.25+9÷(-3)
0.5-3
(5)(-1)4-(1-0.5)3×(-2)4×[2—(—3)2]
解:原式=1-×16×(-7)
1+14
(6)-32+16÷(-2)×+(-1)2020
解:原式=-9-4+1
(7)
(-4)
12
解:原式
×13132
i
494
16
12
(8)-32:2×
3)+4-2×
1)2
解:原式
944
4949
9÷×+4-4×
9××。74~4
20
+4
16
6.简便计算:
(1)
×18-1.45×6+3.95×6
解:原式
×1Q5
×18+×18)
(-1.45+3.95)×6
(14-15+5)+2.5×6
4+15
25
16
(2)75×16
32
25
25
解:原式=(75+
32)×(16×16
25
25)、16
75+
32)×16+(75+
3225
25
1625
16
75×16+×16+75×十
253225
25
1200+=+48+
1261
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
