【沪科版】数学八年级上册 13.2命题与证明第3课时三角形内角和定理的证明及其推论 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 13.2命题与证明第3课时三角形内角和定理的证明及其推论 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览








文档简介
(共26张PPT)
标题截图放置居中位置
课前预习
预习新矢
1.在证明命题时,要分清命题的条件和结论
如果问题与图形有关,首先,根据条件画出图
形,并在图形上标出有关字母与符号;再结合
图形,写出已知、求证;然后,分析因果关
系,找出证明途径;最后有条理地写出证明
过程
2.三角形内角和定理:三角形的内角和等
于180
推论1:直角三角形的两锐角互余
推论2:有两个角互余的三角形是直角
角形
当堂训练
巩固基础
知识点1三角形内角和定理
1.如图,在证明“△ABC内角和等于180”时,延
长BC至点D,过点C作CE∥AB,得到
ABC=ECD, BAC
ACE,由于
∠BCD=180°,可得到∠ABC+∠ACB
BAC=180°,这个证明方法体现的数学思想
A.数形结合
B.特殊到一般
C.一般到特殊
D.转化
B
(第1题图)
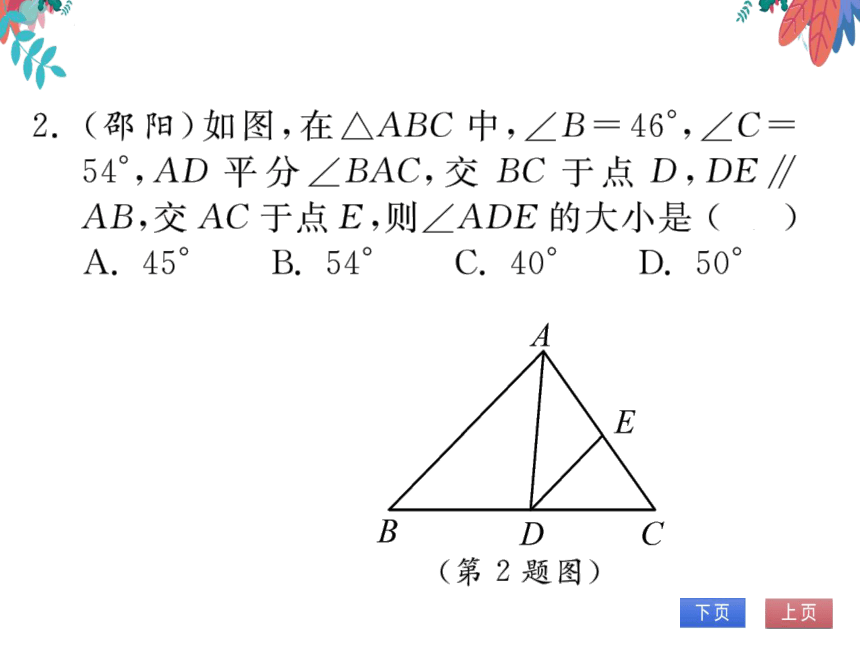
2.(邵阳)如图,在△ABC中,∠B=46°,∠C
54°,AD平分∠BAC,交BC于点D,DE∥
AB,交AC于点E,则∠ADE的大小是(C
A.45°
B.54
C.40°
D.50
(第2题图)
(第3题图)
4.(和县)当三角形中一个内角a是另一个内角B
的两倍时,我们称此三角形为“标准三角形”
其中a为“标准角”.如果一个“标准三角形”的
标准角”为100°,那么这个“标准三角形”的最
小内角度数为
A.30°
B.45
C.50
D.60
(第5题图)
知织点2直角三角形的两锐角互余
6.直角三角形的一个锐角∠A是另一个锐角
∠B的3倍,那么∠B的度数是
A.22.5°B.45°
C.67.5°D.135
第7题图)
8.(遵义)如图,在平行线a,b之间放置一块直角
角尺,三角尺的顶点A,B分别在直线a,b
上,则∠1十∠2的度数为
A
A.90
B.85°
C.80
D.60°
第8题图)
9.(合肥)如图,已知AB∥CD,AE交CD于点
C,DE⊥AE,垂足为E,∠A=37°.求∠D的
度数
解:∵AB∥CD,∠A=37°,
∠DCE=∠A=37°
DE⊥AE,
∠CED=90°
D=90°-∠DCE=90°-37°=53°
标题截图放置居中位置
课前预习
预习新矢
1.在证明命题时,要分清命题的条件和结论
如果问题与图形有关,首先,根据条件画出图
形,并在图形上标出有关字母与符号;再结合
图形,写出已知、求证;然后,分析因果关
系,找出证明途径;最后有条理地写出证明
过程
2.三角形内角和定理:三角形的内角和等
于180
推论1:直角三角形的两锐角互余
推论2:有两个角互余的三角形是直角
角形
当堂训练
巩固基础
知识点1三角形内角和定理
1.如图,在证明“△ABC内角和等于180”时,延
长BC至点D,过点C作CE∥AB,得到
ABC=ECD, BAC
ACE,由于
∠BCD=180°,可得到∠ABC+∠ACB
BAC=180°,这个证明方法体现的数学思想
A.数形结合
B.特殊到一般
C.一般到特殊
D.转化
B
(第1题图)
2.(邵阳)如图,在△ABC中,∠B=46°,∠C
54°,AD平分∠BAC,交BC于点D,DE∥
AB,交AC于点E,则∠ADE的大小是(C
A.45°
B.54
C.40°
D.50
(第2题图)
(第3题图)
4.(和县)当三角形中一个内角a是另一个内角B
的两倍时,我们称此三角形为“标准三角形”
其中a为“标准角”.如果一个“标准三角形”的
标准角”为100°,那么这个“标准三角形”的最
小内角度数为
A.30°
B.45
C.50
D.60
(第5题图)
知织点2直角三角形的两锐角互余
6.直角三角形的一个锐角∠A是另一个锐角
∠B的3倍,那么∠B的度数是
A.22.5°B.45°
C.67.5°D.135
第7题图)
8.(遵义)如图,在平行线a,b之间放置一块直角
角尺,三角尺的顶点A,B分别在直线a,b
上,则∠1十∠2的度数为
A
A.90
B.85°
C.80
D.60°
第8题图)
9.(合肥)如图,已知AB∥CD,AE交CD于点
C,DE⊥AE,垂足为E,∠A=37°.求∠D的
度数
解:∵AB∥CD,∠A=37°,
∠DCE=∠A=37°
DE⊥AE,
∠CED=90°
D=90°-∠DCE=90°-37°=53°
