【沪科版】数学八年级上册 14.2三角形全等的判定4.其他判定两个三角形全等的条件 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 14.2三角形全等的判定4.其他判定两个三角形全等的条件 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览





文档简介
(共25张PPT)
标题截图放置居中位置
课前预习
预新知
1.两角分别相等且其中一组等角的对边
相等的两个三角形全等,可以简记为“角角边”
或“AAS
A=∠A
2.在△ABC和△ABC中
B
B
AC =AO
△ABC≌△ABC
当堂训练
巩固基础
知识点1判定三角形全等的方法—“AAS
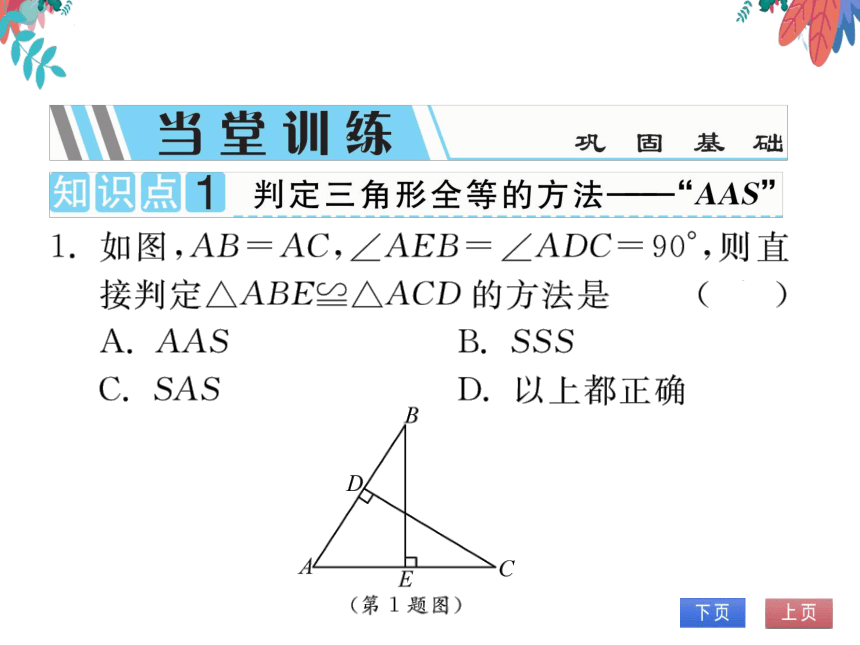
1.如图,AB=AC,∠AEB=∠ADC=90°,则直
接判定△ABE≌△ACD的方法是(A
A AAS
B. SSS
C. SAS
D.以上都正确
(第1题图)
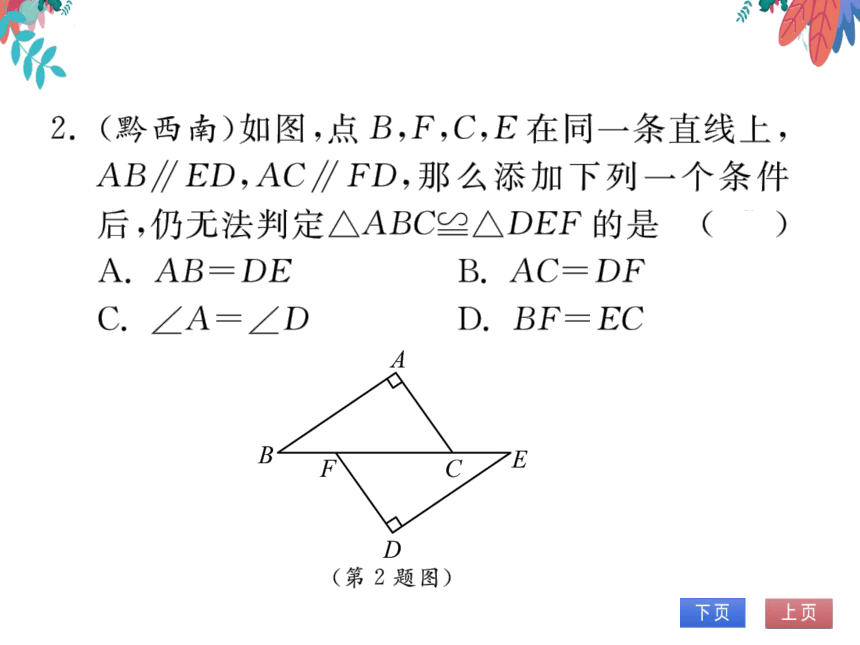
2.(黔西南)如图,点B,F,C,E在同一条直线上,
AB∥ED,AC∥FD,那么添加下列一个条件
后,仍无法判定△ABC≌△DEF的是(C
A=DE
B. AC=DE
C.∠A=∠D
D. BE=EC
D
(第2题图)
3.下列条件中,不能判定△ABC≌△ABC的是
A.AB=AB′,∠A=∠A,AC=AC
B.AB=A'B′,∠A=∠A,∠B=∠B
C.AB=A'B′,∠A=∠A,∠C=∠C
D.∠A=∠A,∠B=∠B,∠C=∠C′
4.(莆田)如图,OP是∠AOB的平分线,点C,D
分别在角的两边OA,OB上,添加下列条件
不能判定△POC≌△POD的选项是
A. PCOA, PD OB B. OC=OD
C.∠OPC=∠OPDD.PC=PD
B
(第4题图)
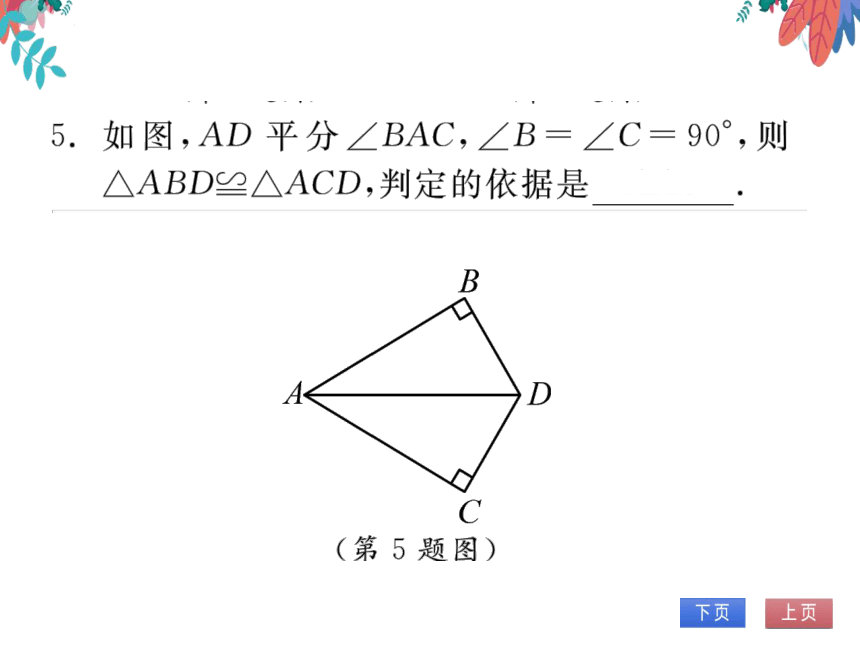
第5题图
6.两边分别相等且其中一组等边的对角相等的
两个三角形不一定(填“一定”或“不
定”,下同)全等,三角分别相等的两个三角形
不一定全等
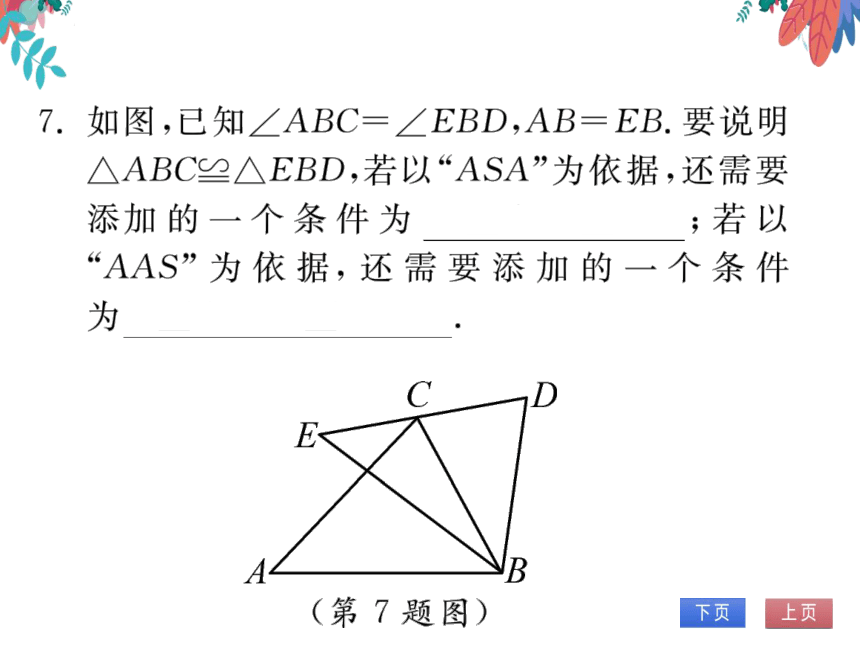
如图,已知∠ABC=∠EBD,AB=EB.要说明
△ABC≌△EBD,若以“ASA”为依据,还需要
添加的一个条件为=∠E;若以
AAS”为依据,还需要添加的一个条件
为∠ACB=∠EDB
(第7题图)
知识点2三角形全等的判定“AAS”的应用
8.如图,在∠AOB的两边上截取OC=OD,连接
AD,BC交于点P,若∠A=∠B,则下列结论
正确的是
①△AOD≌△BOC;②△APC≌△BPD;
③PA=PB
C.①②D.①②③
(第8题图)
(第9题图)
(第10题图)
11.如图,点B,E,C,F在同一条直线上,且
BE=CF,AB∥DE,∠A=∠D.求证:
AC∥DF
证明:BE=CF
BC=EF
AB∥DE,
∠B=∠DEF
又∵∠A=∠D
标题截图放置居中位置
课前预习
预新知
1.两角分别相等且其中一组等角的对边
相等的两个三角形全等,可以简记为“角角边”
或“AAS
A=∠A
2.在△ABC和△ABC中
B
B
AC =AO
△ABC≌△ABC
当堂训练
巩固基础
知识点1判定三角形全等的方法—“AAS
1.如图,AB=AC,∠AEB=∠ADC=90°,则直
接判定△ABE≌△ACD的方法是(A
A AAS
B. SSS
C. SAS
D.以上都正确
(第1题图)
2.(黔西南)如图,点B,F,C,E在同一条直线上,
AB∥ED,AC∥FD,那么添加下列一个条件
后,仍无法判定△ABC≌△DEF的是(C
A=DE
B. AC=DE
C.∠A=∠D
D. BE=EC
D
(第2题图)
3.下列条件中,不能判定△ABC≌△ABC的是
A.AB=AB′,∠A=∠A,AC=AC
B.AB=A'B′,∠A=∠A,∠B=∠B
C.AB=A'B′,∠A=∠A,∠C=∠C
D.∠A=∠A,∠B=∠B,∠C=∠C′
4.(莆田)如图,OP是∠AOB的平分线,点C,D
分别在角的两边OA,OB上,添加下列条件
不能判定△POC≌△POD的选项是
A. PCOA, PD OB B. OC=OD
C.∠OPC=∠OPDD.PC=PD
B
(第4题图)
第5题图
6.两边分别相等且其中一组等边的对角相等的
两个三角形不一定(填“一定”或“不
定”,下同)全等,三角分别相等的两个三角形
不一定全等
如图,已知∠ABC=∠EBD,AB=EB.要说明
△ABC≌△EBD,若以“ASA”为依据,还需要
添加的一个条件为=∠E;若以
AAS”为依据,还需要添加的一个条件
为∠ACB=∠EDB
(第7题图)
知识点2三角形全等的判定“AAS”的应用
8.如图,在∠AOB的两边上截取OC=OD,连接
AD,BC交于点P,若∠A=∠B,则下列结论
正确的是
①△AOD≌△BOC;②△APC≌△BPD;
③PA=PB
C.①②D.①②③
(第8题图)
(第9题图)
(第10题图)
11.如图,点B,E,C,F在同一条直线上,且
BE=CF,AB∥DE,∠A=∠D.求证:
AC∥DF
证明:BE=CF
BC=EF
AB∥DE,
∠B=∠DEF
又∵∠A=∠D
