【沪科版】数学八年级上册 15.3等腰三角形第1课时等腰三角形的性质 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 15.3等腰三角形第1课时等腰三角形的性质 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览





文档简介
(共28张PPT)
标题截图放置居中位置
第4题图
课前预习
习新知
1.等腰三角形的两底角相等.简称“等边对
等角”;这里要注意:“等边对等角”是在同一个
角形中
2.等腰三角形是轴对称图形,对称轴是
顶角平分线所在的直线;等腰三角形底边上的
高
中线及顶角平分线重合(简
称“三线合一”)
当堂训练
巩固基础
知识点1等边对等角
(阜阳)若等腰三角形的一个内角是30°,则顶
角的度数是
A.30°
B.120
C.30°或120°
D.60°
2.(枣庄)如图,在△ABC中,AB=AC,∠A=30°,
E为BC的延长线上一点,∠ABC与∠ACE的
平分线相交于点D,则∠D等于
A.15°
B.17.5°C.20°
D.22.5°
(第2题图)
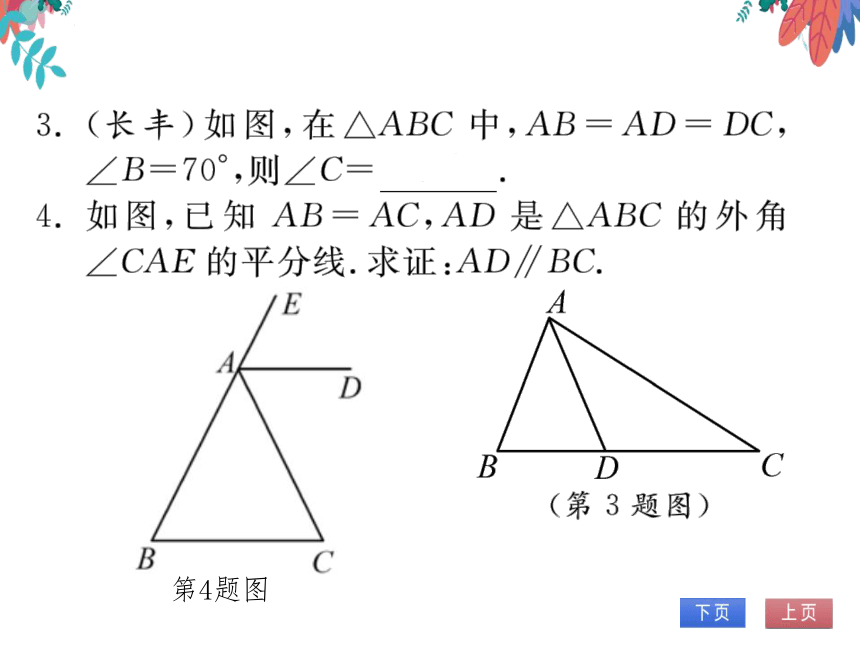
3.(长丰)如图,在△ABC中,AB=AD=DC,
∠B=70°,则∠C
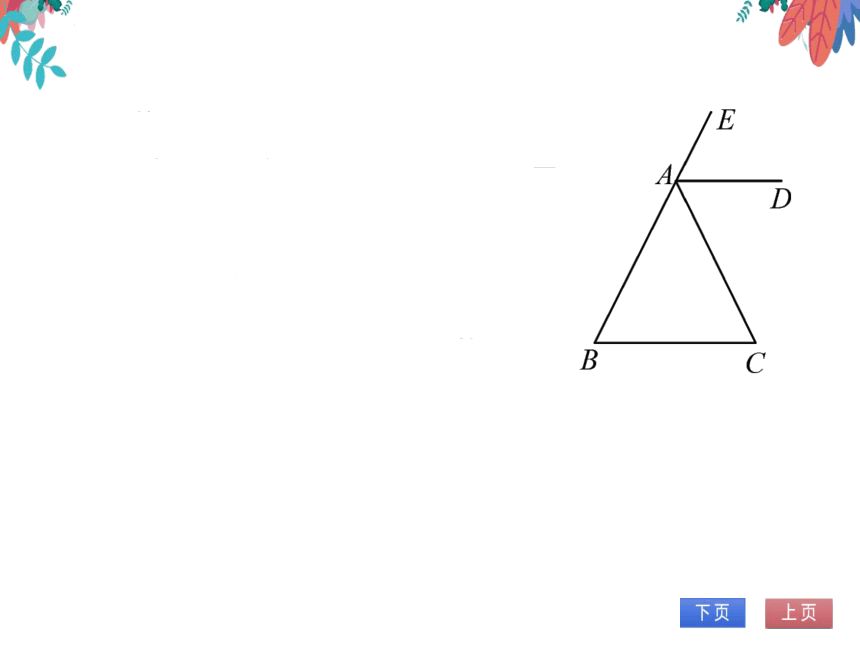
4.如图,已知AB=AC,AD是△ABC的外角
CAE的平分线.求证:AD∥BC
(第3题图)
证明:AB=AC,
B=∠C.又∵∠EAC
B+∠C,∴∠EAC=2∠B
又:AD平分∠EAC,
∠EAC=2∠EAD.
∠EAD=∠B.∴AD∥BC
知识点2等腰三角形的“三线合
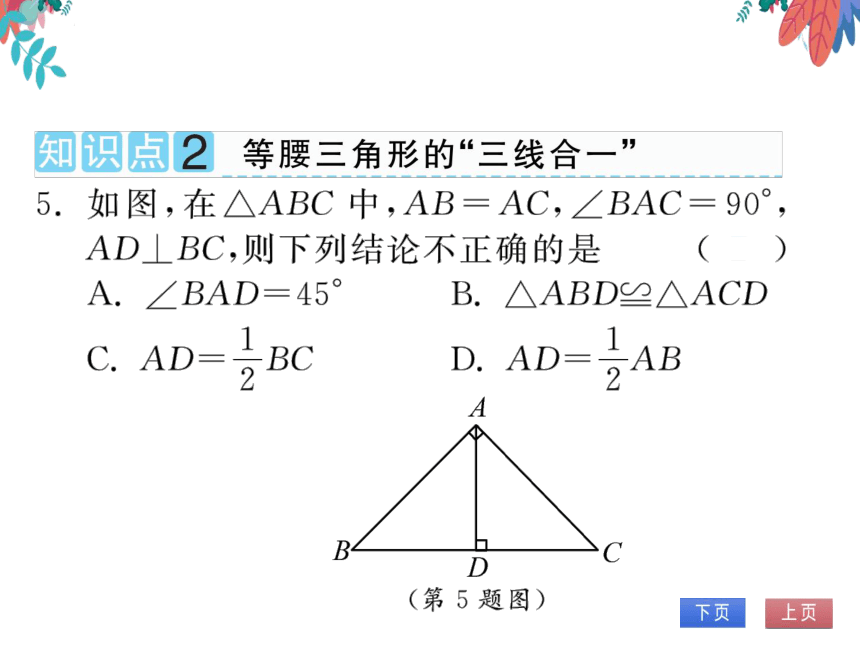
5.如图,在△ABC中,AB=AC,∠BAC=90°
AD⊥BC,则下列结论不正确的是
A.∠BAD=45°
B.△ABD≌△ACD
C. AD I
bc
D.A)1
AB
(第5题图)
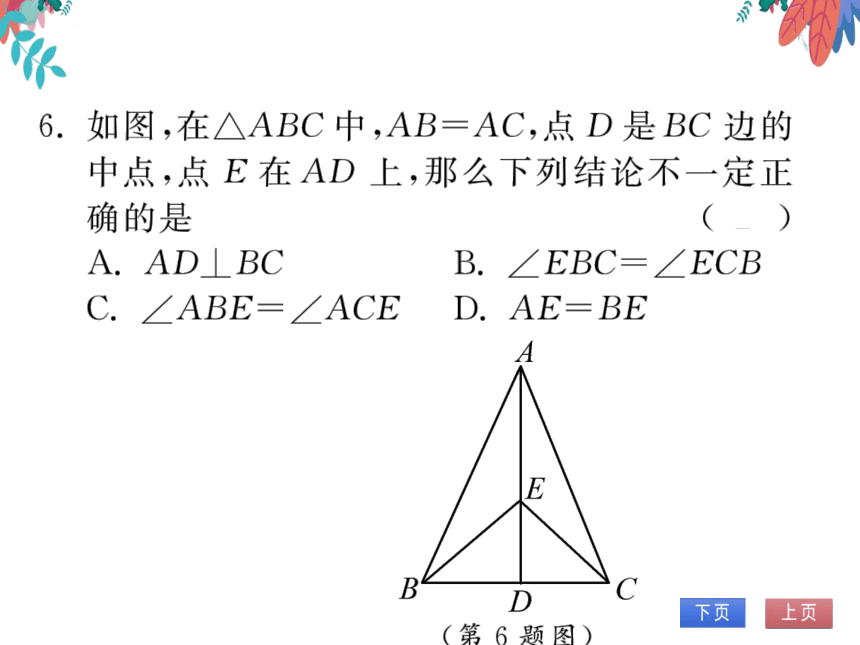
6.如图,在△ABC中,AB=AC,点D是BC边的
中点,点E在AD上,那么下列结论不一定正
确的是
A. AD BC
B.∠EBC=∠ECB
C.∠ABE=∠ACED.AE=BE
(第6题图)
如图,点D,E在△ABC的边BC上,AB
AC,BD=CE.求证:AD=AE
证明:过点A作AF⊥BC于
F.∵AB=AC,AF⊥BC,
BF=CF
又∵BD=CE,
DE=EE
B D E
AF垂直平分线段DE.∴AD=AE
知识点3等边三角形的性质
8.已知△ABC为等边三角形,则∠A的度数是
A.30°
B.45°
C.60
D.90°
9.等边三角形的两条高线相交所成钝角的度数
A.105°B.120°C.135°D.150
标题截图放置居中位置
第4题图
课前预习
习新知
1.等腰三角形的两底角相等.简称“等边对
等角”;这里要注意:“等边对等角”是在同一个
角形中
2.等腰三角形是轴对称图形,对称轴是
顶角平分线所在的直线;等腰三角形底边上的
高
中线及顶角平分线重合(简
称“三线合一”)
当堂训练
巩固基础
知识点1等边对等角
(阜阳)若等腰三角形的一个内角是30°,则顶
角的度数是
A.30°
B.120
C.30°或120°
D.60°
2.(枣庄)如图,在△ABC中,AB=AC,∠A=30°,
E为BC的延长线上一点,∠ABC与∠ACE的
平分线相交于点D,则∠D等于
A.15°
B.17.5°C.20°
D.22.5°
(第2题图)
3.(长丰)如图,在△ABC中,AB=AD=DC,
∠B=70°,则∠C
4.如图,已知AB=AC,AD是△ABC的外角
CAE的平分线.求证:AD∥BC
(第3题图)
证明:AB=AC,
B=∠C.又∵∠EAC
B+∠C,∴∠EAC=2∠B
又:AD平分∠EAC,
∠EAC=2∠EAD.
∠EAD=∠B.∴AD∥BC
知识点2等腰三角形的“三线合
5.如图,在△ABC中,AB=AC,∠BAC=90°
AD⊥BC,则下列结论不正确的是
A.∠BAD=45°
B.△ABD≌△ACD
C. AD I
bc
D.A)1
AB
(第5题图)
6.如图,在△ABC中,AB=AC,点D是BC边的
中点,点E在AD上,那么下列结论不一定正
确的是
A. AD BC
B.∠EBC=∠ECB
C.∠ABE=∠ACED.AE=BE
(第6题图)
如图,点D,E在△ABC的边BC上,AB
AC,BD=CE.求证:AD=AE
证明:过点A作AF⊥BC于
F.∵AB=AC,AF⊥BC,
BF=CF
又∵BD=CE,
DE=EE
B D E
AF垂直平分线段DE.∴AD=AE
知识点3等边三角形的性质
8.已知△ABC为等边三角形,则∠A的度数是
A.30°
B.45°
C.60
D.90°
9.等边三角形的两条高线相交所成钝角的度数
A.105°B.120°C.135°D.150
