【沪科版】数学八年级上册 第15章 专题六 巧用角平分线的性质解题 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 第15章 专题六 巧用角平分线的性质解题 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览







文档简介
(共26张PPT)
标题截图放置居中位置
类型1角平分线作双垂线—利用角平分线的
性质证明线段或角相等
1.如图,在△ABC中,∠C=90°,
AD平分∠BAC,BD=4,BC
则点D到AB的距离是
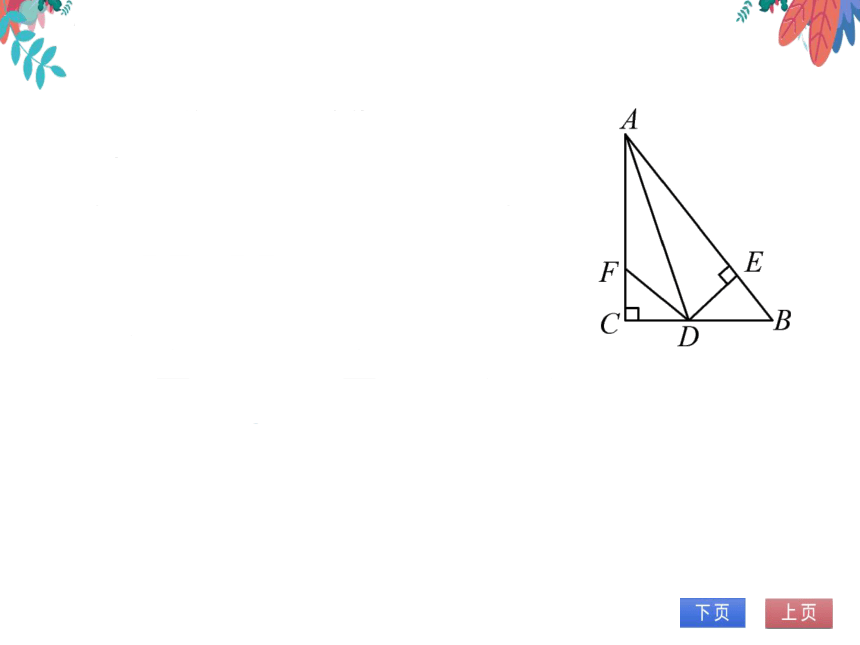
2.(合肥)如图,在△ABC中,AD平分∠BAC,
∠C=90°,DE⊥AB于点E,点F在AC上,
BD=DF
(1)求证:CF=EB;
(2)若AB=12,AF=8,求CF的长
(1)证明:∵AD平分∠BAC,∠C
90°,DE⊥AB,∴DE=DC
在Rt△CDF和Rt△EDB中,
DE=DB
DC- DE
Rt△CDF≌Rt△EDB.(HL)
CFEEB
(2)解:设CF=x,∴AE=12-x,易知
CD=DE
AD=AD
在Rt△ACD和Rt△AED中,
CD= DE
Rt△ACD≌Rt△AED.(HL)
AC=AE,即8+x=12-x,解得x=2,目
CF
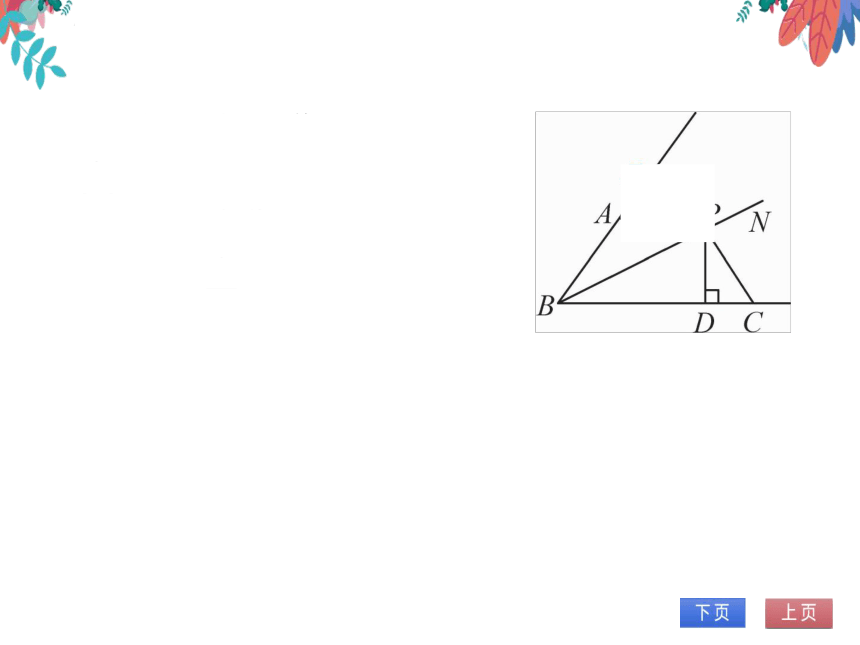
证明:过点P作PE⊥AB于
E
BN平分∠ABC,PE⊥
AB,PD⊥BC,PE=PD.
在Rt△PBE和Rt△PBDB
BP=BP
中
PE=PD,
Rt△PBE≌Rt△PBD.(HL)BE=BD
AB+=2BD, BC=CD BD, AB- BE
AE.AE=CD
PE=PD
在△PAE和△PCD中,∠PEB=∠PDC,
AE=CD
△PAE≌△PCD.∴.∠BCP=∠EAP.
BAP+∠EAP=180°
∠BAP+∠BCP=180
类型2角平分线截全等—以角平分线为对称
轴构造全等三角形
4.(1)如图①,在Rt△ABC中,∠C=90°,∠B
45°,AD平分∠BAC,交BC于点D.如果
作辅助线DE⊥AB于点E,则可以得到AC,
D,AB三条线段之间的数量关系为
AB=+CD
(2)如图②,在△ABC中,∠C=2∠B,AD平
分∠BAC,交BC于点D,(1)中的结论是
否仍然成立 若不成立,试说明理由;若成
请证明.
E
F
B O
B
D
解:(2)成立,证明:在AB上取一点F,使AF
AC,连接DF
AD平分∠BAC,∠CAD=∠FAD
AC=AF
在△ACD和△AFD中
CAD=∠FAD
AD=AD
ACD≌△AFD
CD=DF,∠C=∠AFD
标题截图放置居中位置
类型1角平分线作双垂线—利用角平分线的
性质证明线段或角相等
1.如图,在△ABC中,∠C=90°,
AD平分∠BAC,BD=4,BC
则点D到AB的距离是
2.(合肥)如图,在△ABC中,AD平分∠BAC,
∠C=90°,DE⊥AB于点E,点F在AC上,
BD=DF
(1)求证:CF=EB;
(2)若AB=12,AF=8,求CF的长
(1)证明:∵AD平分∠BAC,∠C
90°,DE⊥AB,∴DE=DC
在Rt△CDF和Rt△EDB中,
DE=DB
DC- DE
Rt△CDF≌Rt△EDB.(HL)
CFEEB
(2)解:设CF=x,∴AE=12-x,易知
CD=DE
AD=AD
在Rt△ACD和Rt△AED中,
CD= DE
Rt△ACD≌Rt△AED.(HL)
AC=AE,即8+x=12-x,解得x=2,目
CF
证明:过点P作PE⊥AB于
E
BN平分∠ABC,PE⊥
AB,PD⊥BC,PE=PD.
在Rt△PBE和Rt△PBDB
BP=BP
中
PE=PD,
Rt△PBE≌Rt△PBD.(HL)BE=BD
AB+=2BD, BC=CD BD, AB- BE
AE.AE=CD
PE=PD
在△PAE和△PCD中,∠PEB=∠PDC,
AE=CD
△PAE≌△PCD.∴.∠BCP=∠EAP.
BAP+∠EAP=180°
∠BAP+∠BCP=180
类型2角平分线截全等—以角平分线为对称
轴构造全等三角形
4.(1)如图①,在Rt△ABC中,∠C=90°,∠B
45°,AD平分∠BAC,交BC于点D.如果
作辅助线DE⊥AB于点E,则可以得到AC,
D,AB三条线段之间的数量关系为
AB=+CD
(2)如图②,在△ABC中,∠C=2∠B,AD平
分∠BAC,交BC于点D,(1)中的结论是
否仍然成立 若不成立,试说明理由;若成
请证明.
E
F
B O
B
D
解:(2)成立,证明:在AB上取一点F,使AF
AC,连接DF
AD平分∠BAC,∠CAD=∠FAD
AC=AF
在△ACD和△AFD中
CAD=∠FAD
AD=AD
ACD≌△AFD
CD=DF,∠C=∠AFD
