【沪科版】数学八年级上册 第13章 专题四 与三角形有关的角度计算 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 第13章 专题四 与三角形有关的角度计算 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览







文档简介
(共25张PPT)
标题截图放置居中位置
类型1根据三角形内角和定理及推论直接计算
角度
1.(阜阳)如图,点D在△ABC的边BC的延长
线上,CE平分∠ACD,∠A=80°,∠B=40°,
则∠ACE的大小是60
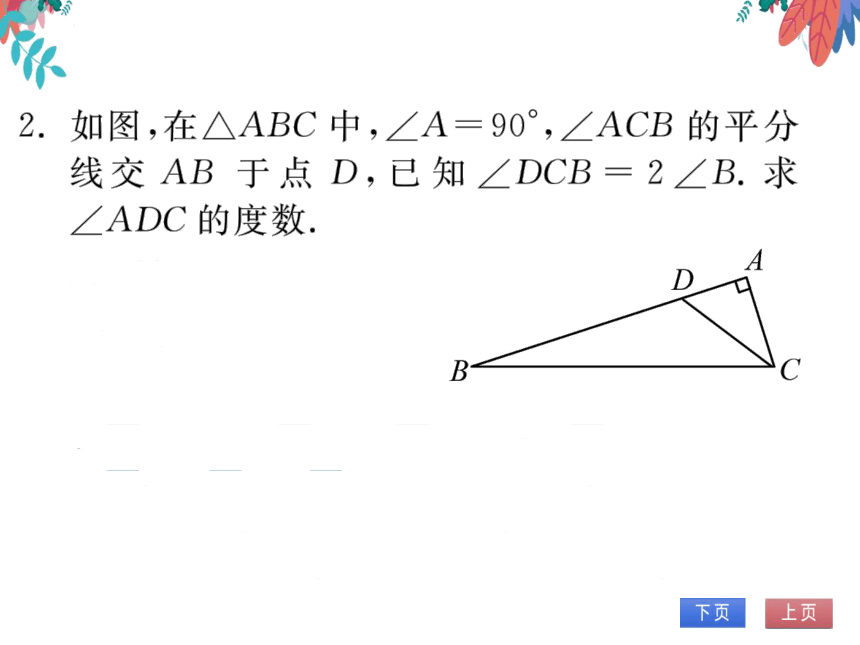
2.如图,在△ABC中,∠A=90°,∠ACB的平分
线交AB于点D,已知∠DCB=2∠B.求
∠ADC的度数
解
ACB的平分
线交AB于点D,
ACD=∠BCD.
DCB=2∠B,∴∠ACD=2∠B
∠A+∠B+∠ACB=180°,
90°+∠B+2∠B+2∠B=180°
∠B=18°.∴.∠ACD=36°
∠ADC=180°-∠A-∠ACD=54°
3.在△ABC中,∠B=55°,且3∠A=∠B+∠C
求∠A和∠C的度数
解:∠A+∠B+∠C=180°,3∠A=∠B+∠C,
4∠A=180°,解得∠A=45°
B=5
C=180-∠A-∠B=180°-4
55=80
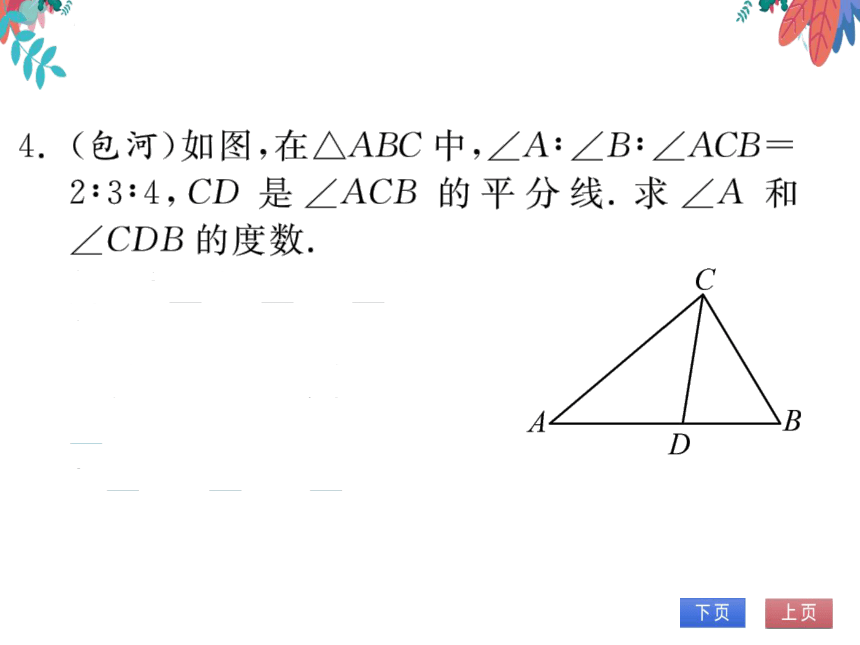
4.(包河)如图,在△ABC中,∠A:∠B:∠ACB
2:3:4,CD是∠ACB的平分线.求∠A和
CDB的度数
解
A:∠B:∠ACB
2:3:4
设∠A=2x,则∠B=3
∠ACB=4,x
A+∠B+∠ACB=180°
2x+3x+4x=180°,解得x=20°
∠A=40°,∠ACB=80°,∠B=60°
CD是∠ACB的平分线
∠BCD=∠ACB=40°
CDB=180°-∠B-∠BCD=180°-60°
40=80
5.如图,平面上六个点A,B,C,D,E,F构成一个
封闭折线图形.求∠A+∠B+∠C+∠D
∠E+∠F的和
解:根据三角形的一个外角A
B
等于与它不相邻的两个内角
C
的和,
∠A+∠B=∠3,∠C+
D=∠1,∠E+∠F=∠2
又∵∠1,∠2,∠3是同一个三角形的三个
外角,
(180°
1)+(180
2)+(180
∠3)=180
∠1+∠2+∠3=360°
A+∠B+∠C+∠D+∠E+∠F=360
类型2以三角尺为背景应用三角形内角和定理
求度数
6.如图,若线段CD平分含30°角的三角尺ABC
的直角,已知∠A=30°,则∠1等于(B)
A.110°B.105°C.100。D.95°
标题截图放置居中位置
类型1根据三角形内角和定理及推论直接计算
角度
1.(阜阳)如图,点D在△ABC的边BC的延长
线上,CE平分∠ACD,∠A=80°,∠B=40°,
则∠ACE的大小是60
2.如图,在△ABC中,∠A=90°,∠ACB的平分
线交AB于点D,已知∠DCB=2∠B.求
∠ADC的度数
解
ACB的平分
线交AB于点D,
ACD=∠BCD.
DCB=2∠B,∴∠ACD=2∠B
∠A+∠B+∠ACB=180°,
90°+∠B+2∠B+2∠B=180°
∠B=18°.∴.∠ACD=36°
∠ADC=180°-∠A-∠ACD=54°
3.在△ABC中,∠B=55°,且3∠A=∠B+∠C
求∠A和∠C的度数
解:∠A+∠B+∠C=180°,3∠A=∠B+∠C,
4∠A=180°,解得∠A=45°
B=5
C=180-∠A-∠B=180°-4
55=80
4.(包河)如图,在△ABC中,∠A:∠B:∠ACB
2:3:4,CD是∠ACB的平分线.求∠A和
CDB的度数
解
A:∠B:∠ACB
2:3:4
设∠A=2x,则∠B=3
∠ACB=4,x
A+∠B+∠ACB=180°
2x+3x+4x=180°,解得x=20°
∠A=40°,∠ACB=80°,∠B=60°
CD是∠ACB的平分线
∠BCD=∠ACB=40°
CDB=180°-∠B-∠BCD=180°-60°
40=80
5.如图,平面上六个点A,B,C,D,E,F构成一个
封闭折线图形.求∠A+∠B+∠C+∠D
∠E+∠F的和
解:根据三角形的一个外角A
B
等于与它不相邻的两个内角
C
的和,
∠A+∠B=∠3,∠C+
D=∠1,∠E+∠F=∠2
又∵∠1,∠2,∠3是同一个三角形的三个
外角,
(180°
1)+(180
2)+(180
∠3)=180
∠1+∠2+∠3=360°
A+∠B+∠C+∠D+∠E+∠F=360
类型2以三角尺为背景应用三角形内角和定理
求度数
6.如图,若线段CD平分含30°角的三角尺ABC
的直角,已知∠A=30°,则∠1等于(B)
A.110°B.105°C.100。D.95°
