【沪科版】数学八年级上册 第14章 专题五 证明三角形全等的基本方法归纳 习题课件
文档属性
| 名称 | 【沪科版】数学八年级上册 第14章 专题五 证明三角形全等的基本方法归纳 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:13 | ||
图片预览




文档简介
(共25张PPT)
标题截图放置居中位置
类型1已知两边对应相等,找第三边或找夹角
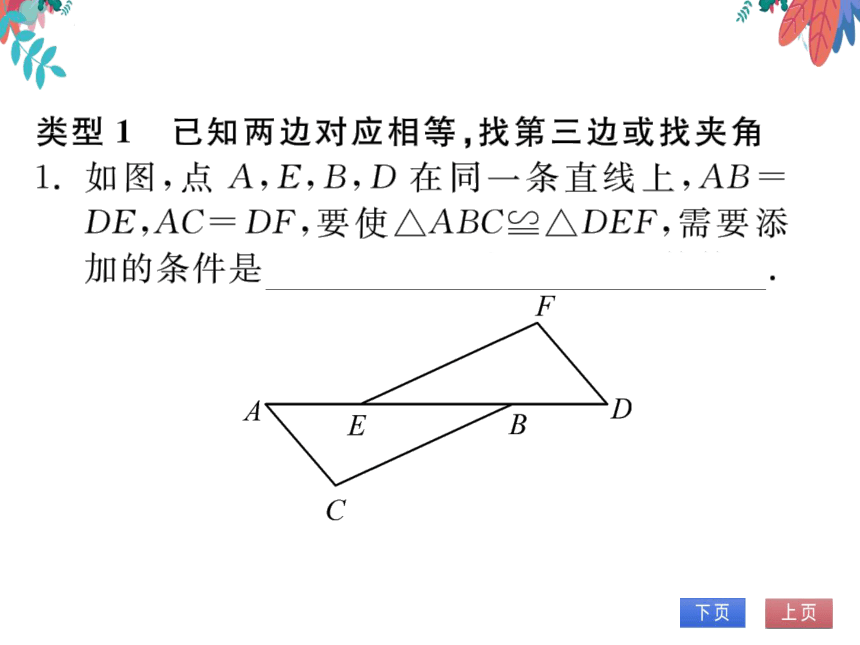
1.如图,点A,E,B,D在同一条直线上,AB
DE,AC=DF,要使△ABC≌△DEF,需要添
加的条件是∠A=∠D或CB=EF等等
2.如图,已知AB=DE,AD=EC,点D是BC的
中点.求证:△ABD≌△EDC
证明:∵点D是BC的中
,(已知
BD=CD
在△ABD和△EDC中
AB=ED,(已知)
AD=EC,(已知
BD=DC,(已证)
△ABD≌△EDC.(SSS
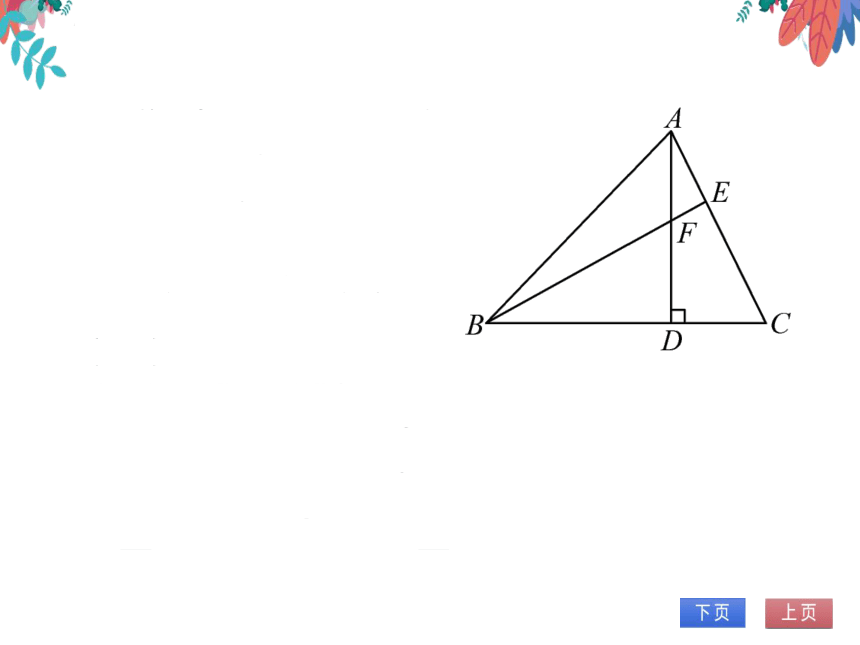
证明:在Rt△BFD和
Rt△ACD中,
BF=AC
FD=CD
∴Rt△BFD≌Rt△ACD
(HD
∠EBC=∠CAD.
CAD+∠C=90
∠EBC+∠C=90°
∠BEC=90°.∴BE⊥AC.
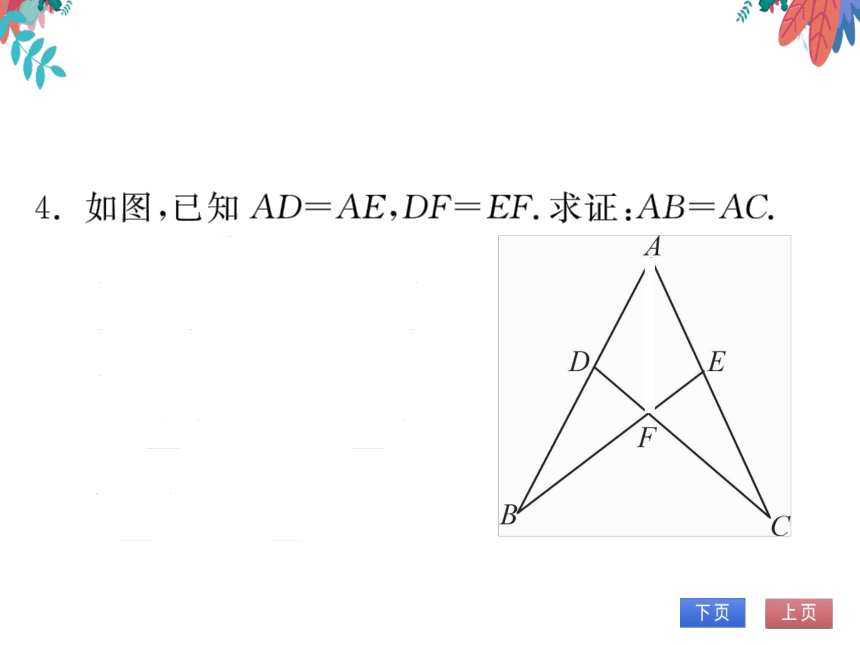
4.如图,知AD=AE,DF=EF.求证:AB=AC
证明:连接AF
在△ADF和△AEF中
AD=AE DF=EF AF
E
AF
△ADF
△AEF
(SSS)
∠ADF=∠AEF
在△ABE和△ACD中
BAE=∠CAD,AE=AD,∠AEB=∠ADC,
△ABE≌△ACD.(ASA)
AB=Ac
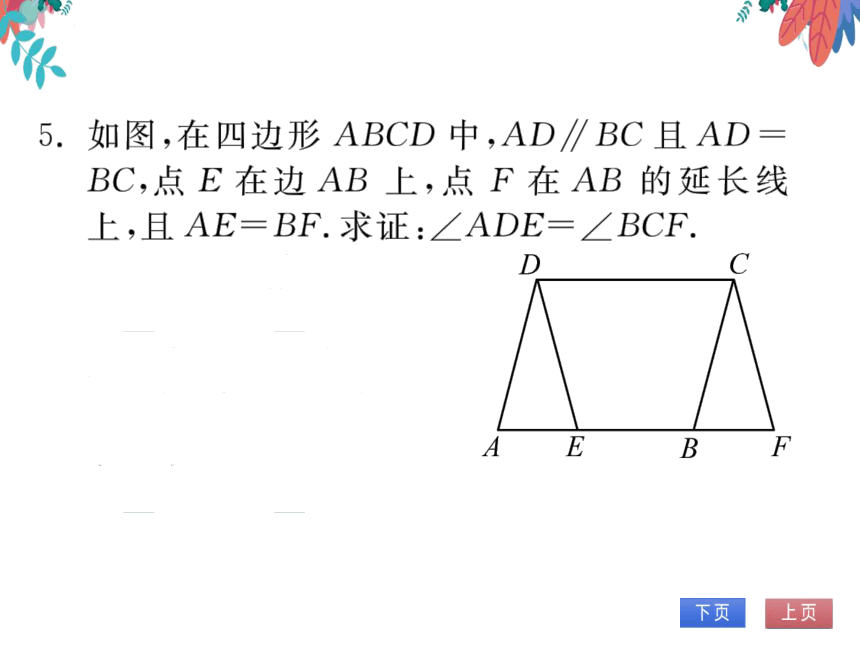
5.如图,在四边形ABCD中,AD∥BC且AD
BC,点E在边AB上,点F在AB的延长线
上,且AE=BF.求证:∠ADE=∠BCF
证明:∵AD∥BC
∠DAE=∠CBF.
又∵AD=BC,AE=BF,
DAE
△CBF.
(SAS)
ADE=∠BCF.
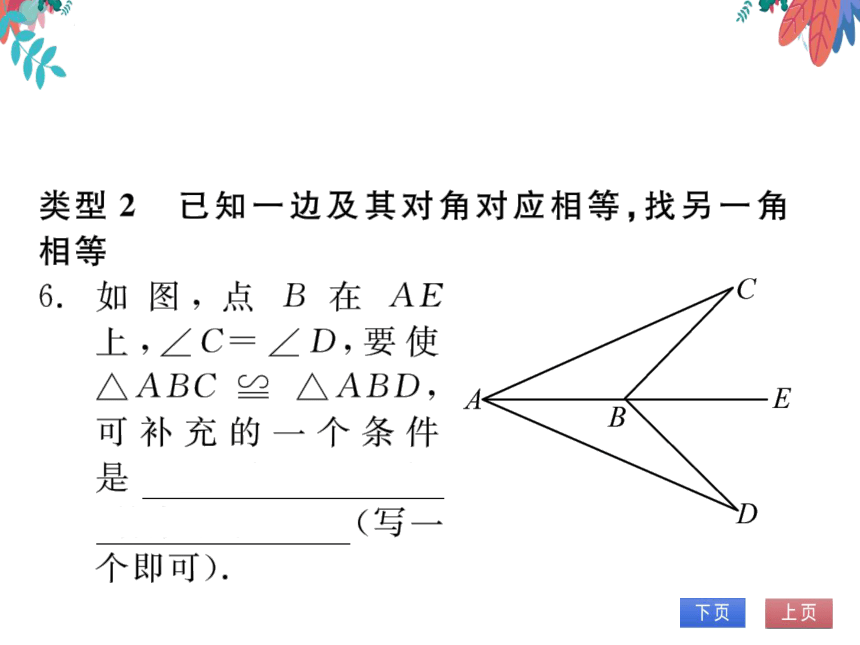
类型2已知一边及其对角对应相等,找另一角
相等
6.如图,点B在AE
上,∠C=∠D,要使
△ABC≌△ABD
可补充的一个条件
是
CAB=∠DAB
(答案不唯一)(写
个即可
证明:AD是△ABC
的中线,
。BD=CD
BE⊥AD,CF⊥AD,
E
BED
CFD
F
又∵∠BDE=∠CDF,
△DBE≌△DCF.(AAS)
BE=CF
8.如图,CA=CD,∠B=∠E,∠BCE=∠ACD
求证:AB=DE
证明:
BCE
ACD
ACB=∠DCE
在△ABC和△DEC中,
∠ACB=∠DCE,
B=∠E,CA=CD,
类型3已知一边及其邻角对应相等,找另一角
或夹该角的另一边相等
9.如图,D是AC上一点,AB=DA,DE∥AB,
B=∠DAE.求证:ABC≌△DAE
标题截图放置居中位置
类型1已知两边对应相等,找第三边或找夹角
1.如图,点A,E,B,D在同一条直线上,AB
DE,AC=DF,要使△ABC≌△DEF,需要添
加的条件是∠A=∠D或CB=EF等等
2.如图,已知AB=DE,AD=EC,点D是BC的
中点.求证:△ABD≌△EDC
证明:∵点D是BC的中
,(已知
BD=CD
在△ABD和△EDC中
AB=ED,(已知)
AD=EC,(已知
BD=DC,(已证)
△ABD≌△EDC.(SSS
证明:在Rt△BFD和
Rt△ACD中,
BF=AC
FD=CD
∴Rt△BFD≌Rt△ACD
(HD
∠EBC=∠CAD.
CAD+∠C=90
∠EBC+∠C=90°
∠BEC=90°.∴BE⊥AC.
4.如图,知AD=AE,DF=EF.求证:AB=AC
证明:连接AF
在△ADF和△AEF中
AD=AE DF=EF AF
E
AF
△ADF
△AEF
(SSS)
∠ADF=∠AEF
在△ABE和△ACD中
BAE=∠CAD,AE=AD,∠AEB=∠ADC,
△ABE≌△ACD.(ASA)
AB=Ac
5.如图,在四边形ABCD中,AD∥BC且AD
BC,点E在边AB上,点F在AB的延长线
上,且AE=BF.求证:∠ADE=∠BCF
证明:∵AD∥BC
∠DAE=∠CBF.
又∵AD=BC,AE=BF,
DAE
△CBF.
(SAS)
ADE=∠BCF.
类型2已知一边及其对角对应相等,找另一角
相等
6.如图,点B在AE
上,∠C=∠D,要使
△ABC≌△ABD
可补充的一个条件
是
CAB=∠DAB
(答案不唯一)(写
个即可
证明:AD是△ABC
的中线,
。BD=CD
BE⊥AD,CF⊥AD,
E
BED
CFD
F
又∵∠BDE=∠CDF,
△DBE≌△DCF.(AAS)
BE=CF
8.如图,CA=CD,∠B=∠E,∠BCE=∠ACD
求证:AB=DE
证明:
BCE
ACD
ACB=∠DCE
在△ABC和△DEC中,
∠ACB=∠DCE,
B=∠E,CA=CD,
类型3已知一边及其邻角对应相等,找另一角
或夹该角的另一边相等
9.如图,D是AC上一点,AB=DA,DE∥AB,
B=∠DAE.求证:ABC≌△DAE
