【沪科版】数学九年级上册 22.2 相似三角形的判定 第3课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 22.2 相似三角形的判定 第3课时 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览




文档简介
(共20张PPT)
课前预习
预习新知
1.如果一个三角形的两条边与另一个三角形的
两条边对应成比例,并且夹角相等
那么这两个三角形相似(可简单说成:两边
成比例且夹角相等的两个三角形
相似
AB
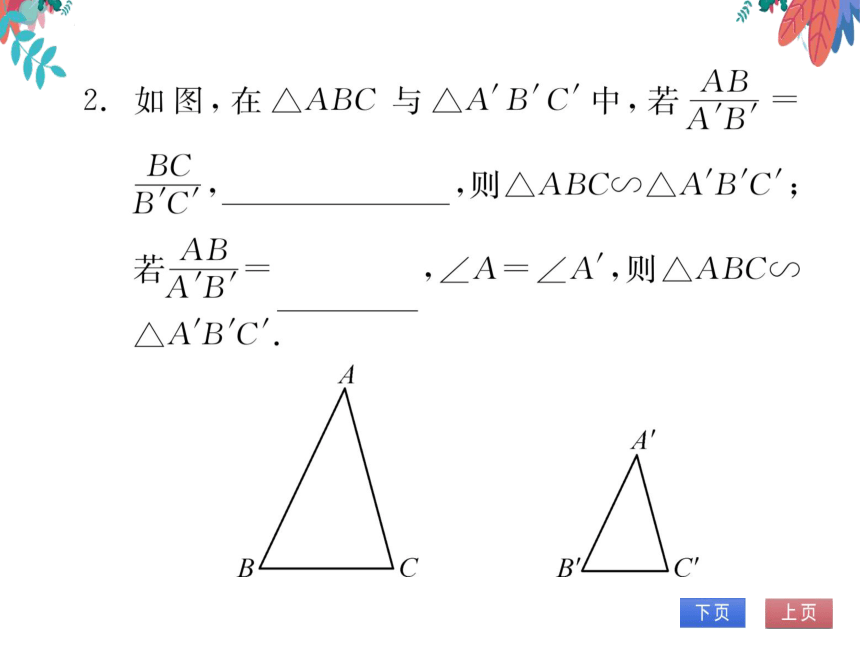
2.如图,在△ABC与△ABC中,看AB
BC,∠B=∠B,则△ABC∽△ABC;
AB
AC
A'C
∠A=∠A,则△ABC
△ABC
B
B
当堂训练
巩固基础
知识点两边成比例且夹角相等的两个三角形相似
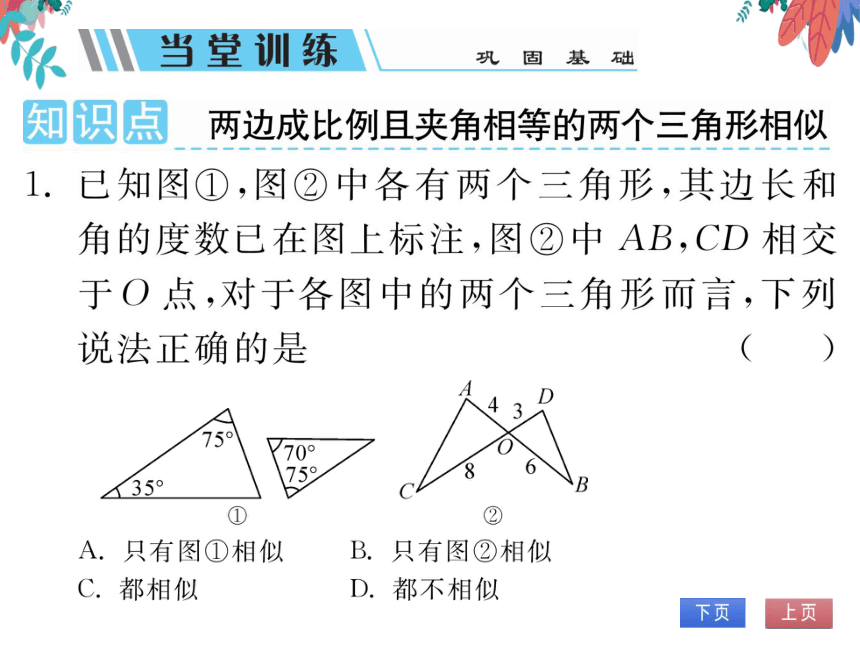
1.已知图①,图②中各有两个三角形,其边长和
角的度数已在图上标注,图②中AB,CD相交
于O点,对于各图中的两个三角形而言,下列
兑法正确的是
75°
70°
75
6
35
A.只有图①相似B.只有图②相似
都相似
D.都不相似
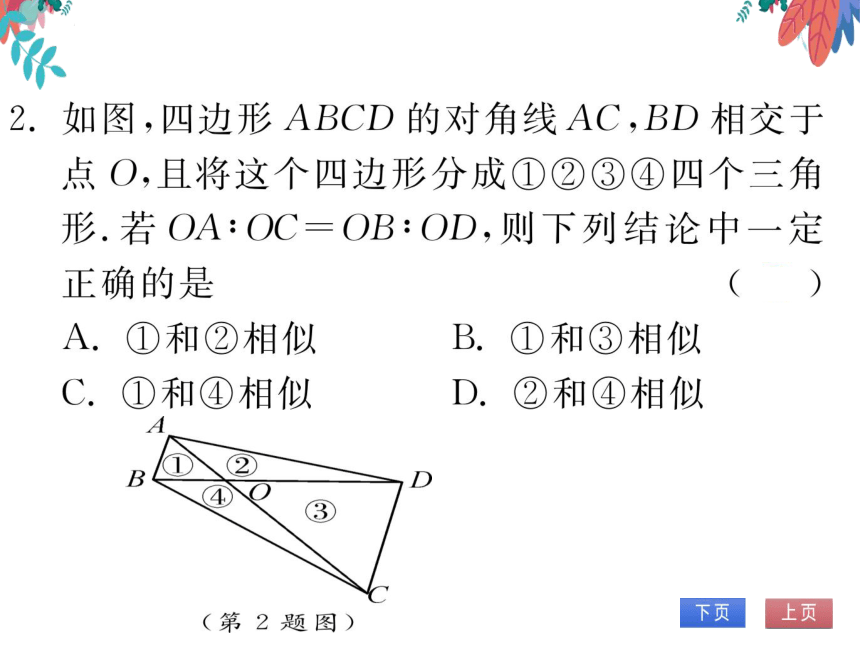
2.如图,四边形ABCD的对角线AC,BD相交于
点O,且将这个四边形分成①②③④四个三角
形.若OA:OC=OB:OD,则下列结论中一定
正确的是
B
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
2
B
3
(第2题图)
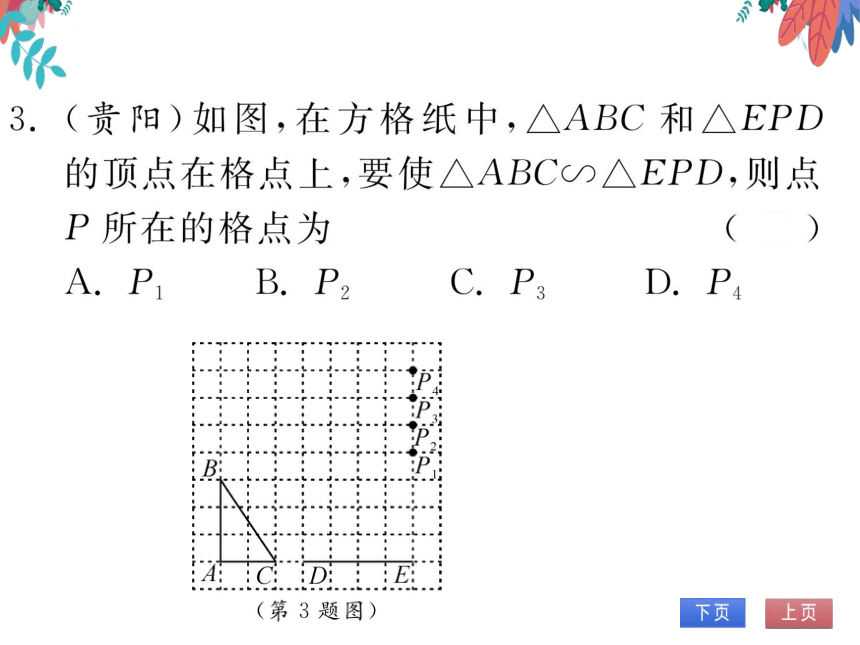
(贵阳)如图,在方格纸中,△ABC和△EPD
的顶点在格点上,要使△ABC∽△EPD,则点
P所在的格点为
B. P
D. P
4
B
第3题图
4.如图,给出下列条件:①∠B=∠ACD;
Ac AB
②∠ADC
ACB;③
cd BO
④AC
AD·AB.其中单独能够判定△ABC∽
△ACD的有
B
A.1个B.2个C.3个D.4个
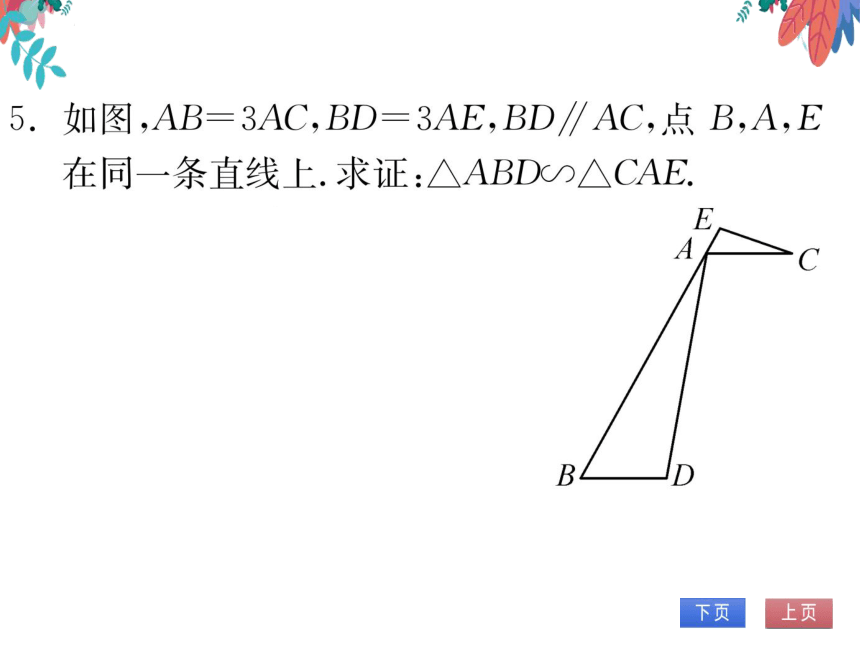
图,AB=3AC,BD=3AE,BD∥AC,点B,A,E
在同一条直线上.求证:△ABD△CAE
证明:BD∥AC,点B,A,E
在同一条直线上,
∠B=∠CAE
AB BD
又·CAAE
ABD△CAE
B
证明:∵△ABC为正三角形
∠A=∠C=60°,BC=AB
D
AE=BE,∴CB=2AE.
AD 1
CD=2AD.B
AD AE 1
CD cB 2
又∵∠A=∠C
AEDC△CBD
课后作业
全面提升
1.如图,∠AOD=90°,OA=OB=BC=CD,那么
下列结论成立的是
B
D
A.△OAB∽△OCAB.△OAB∽△ODA
C.△BAC∽△BDAD.以上结论都不成立
2.如图,点E是正方形ABCD的边CD的中点,
F是BC边上的一点,补充下列条件之一:
①∠AED=∠CFE;②AE⊥FE;③BF:FC
3:1;④AE:EF=2:1.能判定△ADE∽△ECF
的有
B.2个C.3
D.4个
课前预习
预习新知
1.如果一个三角形的两条边与另一个三角形的
两条边对应成比例,并且夹角相等
那么这两个三角形相似(可简单说成:两边
成比例且夹角相等的两个三角形
相似
AB
2.如图,在△ABC与△ABC中,看AB
BC,∠B=∠B,则△ABC∽△ABC;
AB
AC
A'C
∠A=∠A,则△ABC
△ABC
B
B
当堂训练
巩固基础
知识点两边成比例且夹角相等的两个三角形相似
1.已知图①,图②中各有两个三角形,其边长和
角的度数已在图上标注,图②中AB,CD相交
于O点,对于各图中的两个三角形而言,下列
兑法正确的是
75°
70°
75
6
35
A.只有图①相似B.只有图②相似
都相似
D.都不相似
2.如图,四边形ABCD的对角线AC,BD相交于
点O,且将这个四边形分成①②③④四个三角
形.若OA:OC=OB:OD,则下列结论中一定
正确的是
B
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
2
B
3
(第2题图)
(贵阳)如图,在方格纸中,△ABC和△EPD
的顶点在格点上,要使△ABC∽△EPD,则点
P所在的格点为
B. P
D. P
4
B
第3题图
4.如图,给出下列条件:①∠B=∠ACD;
Ac AB
②∠ADC
ACB;③
cd BO
④AC
AD·AB.其中单独能够判定△ABC∽
△ACD的有
B
A.1个B.2个C.3个D.4个
图,AB=3AC,BD=3AE,BD∥AC,点B,A,E
在同一条直线上.求证:△ABD△CAE
证明:BD∥AC,点B,A,E
在同一条直线上,
∠B=∠CAE
AB BD
又·CAAE
ABD△CAE
B
证明:∵△ABC为正三角形
∠A=∠C=60°,BC=AB
D
AE=BE,∴CB=2AE.
AD 1
CD=2AD.B
AD AE 1
CD cB 2
又∵∠A=∠C
AEDC△CBD
课后作业
全面提升
1.如图,∠AOD=90°,OA=OB=BC=CD,那么
下列结论成立的是
B
D
A.△OAB∽△OCAB.△OAB∽△ODA
C.△BAC∽△BDAD.以上结论都不成立
2.如图,点E是正方形ABCD的边CD的中点,
F是BC边上的一点,补充下列条件之一:
①∠AED=∠CFE;②AE⊥FE;③BF:FC
3:1;④AE:EF=2:1.能判定△ADE∽△ECF
的有
B.2个C.3
D.4个
