【沪科版】数学九年级上册 22.2 相似三角形的判定 第5课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 22.2 相似三角形的判定 第5课时 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
课前预习
颍习新知
如果一个直角三角形的斜边和一条直角边与另
个直角三角形的斜边和一条直角边
对应成比例,那么这两个直角三角形相似
2.在Rt△ABC和Rt△ABC中,∠A=∠A
90°,若AB=1,BC=2,AB=2,BC=4,则
ABC与△ABC相似
当堂训练
巩固基础
知识点直角三角形相似的判定
1.已知两个直角三角形的斜边和一条直角边分
别为7,3和21,9,则这两个直角三角形(A
A.一定相似
定不相似
C.不一定相似
D.以上都不对
B
B
A.∠A=∠A=40° R AC BO
AC′BC
AC AC
AC AB
AB
ab B
果一个直角三角形的两条边长分别是6和
8,另一个与它相似的直角三角形的边长分别
是3和4及x,那么x的值
A.只有1个
B.可以有2个
C.有2个以上但有限D.有无数个
4.在△ABC和△DEF中,∠C=∠E=90°,AC
3,AB=7,FE=12,DF=28,则△ABC∽
△FDE
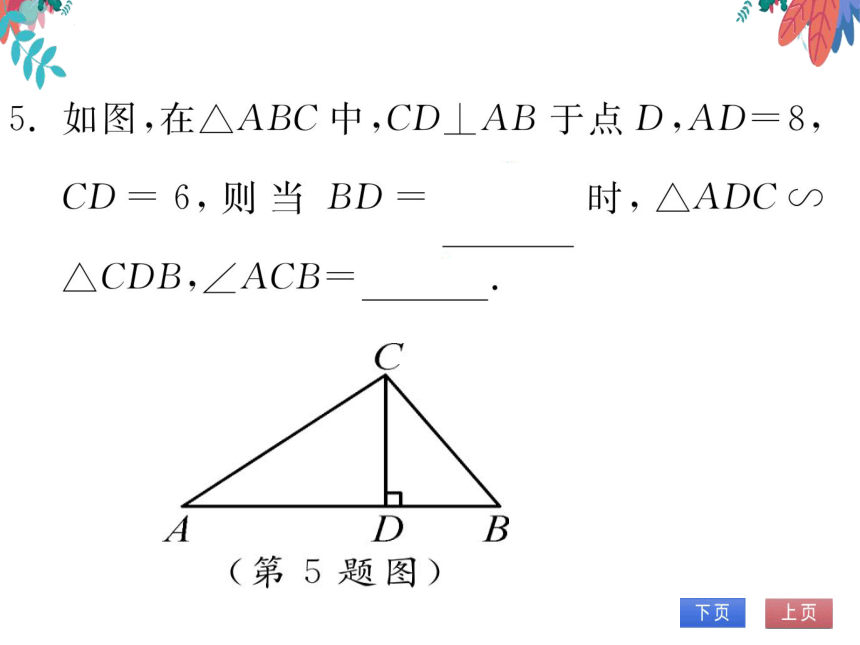
如图,在△ABC中,CD⊥AB于点D,AD=8,
CD=6,则当BD
时,△ADC
△CDB,∠ACB=90
d B
(第5题图)
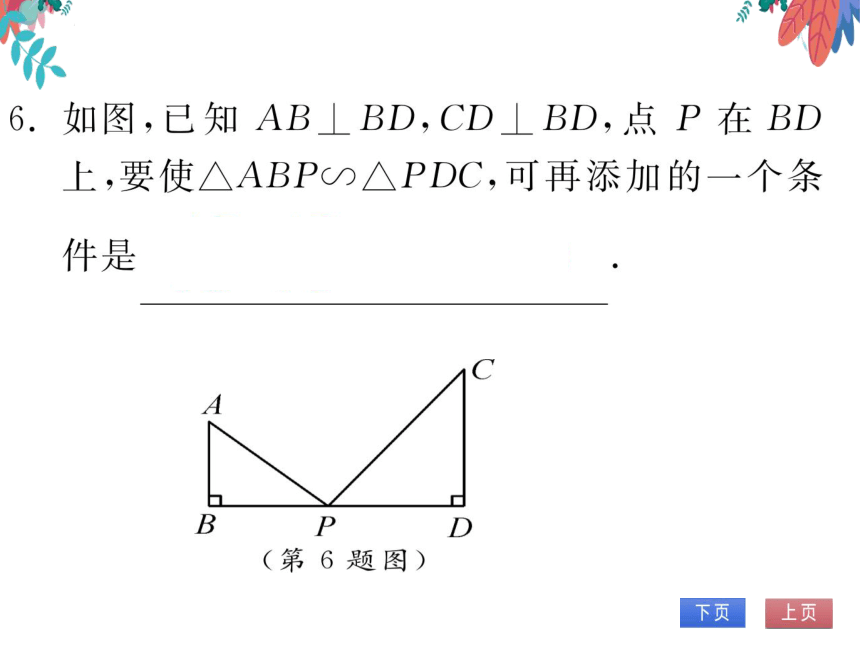
如图,已知AB⊥BD,CD⊥BD,点P在BD
上,要使△ABP∽△PDC,可再添加的一个条
AB AP
件是
PDp(答案不唯一)
(旁
题多)
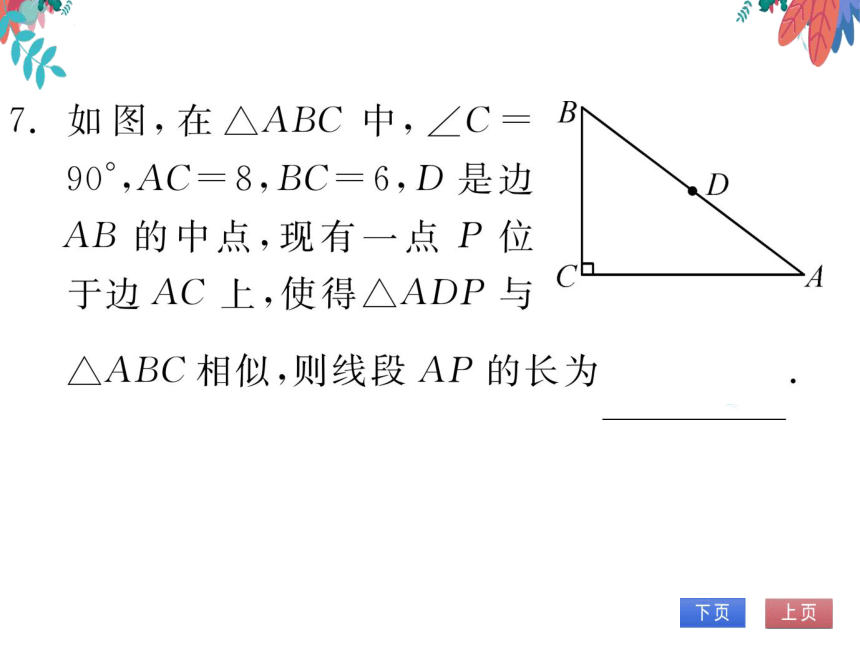
图,在△ABC中,∠C=B
90°,AC=8,BC=6,D是边
AB的中点,现有
P位
于边AC上,使得△ADP与
△ABC相似,则线段AP的长为4或
4
8.如图,在△ABC中,AC=3,BC=4,AB=5,在
△DEF中,∠F=90°,DF=6,DE=10.求证
△ABC∽△DEF
B
证明:∵在△ABC中,AC=3,BC=4,AB=5
AC2BCZ=AB2
∠C=90°
在Rt△ABC和Rt△DEF中
AC AB 1
DEDE 2
Rt△ ABOrt△DEF,即△ABC∽△DEF
9.如图,在△ABC中,AC=8cm,BC=6cm
AB=10cm,D是AB上一点,AD=4cm
DE⊥AB交AC于点E,当AE的长为多少
时,△ADE与△ABC相似
解:∵AC=8cm,BC=6cm,
AB-10 cm
AC2BC2=AB2
E
∠C=90°
又∵DE⊥AB,
∠ADE=90°
AD AE
AC AB
4 AE
即当
时,△ADE∽△ACB
当AE=5cm时,△ADE∽△ACB
课前预习
颍习新知
如果一个直角三角形的斜边和一条直角边与另
个直角三角形的斜边和一条直角边
对应成比例,那么这两个直角三角形相似
2.在Rt△ABC和Rt△ABC中,∠A=∠A
90°,若AB=1,BC=2,AB=2,BC=4,则
ABC与△ABC相似
当堂训练
巩固基础
知识点直角三角形相似的判定
1.已知两个直角三角形的斜边和一条直角边分
别为7,3和21,9,则这两个直角三角形(A
A.一定相似
定不相似
C.不一定相似
D.以上都不对
B
B
A.∠A=∠A=40° R AC BO
AC′BC
AC AC
AC AB
AB
ab B
果一个直角三角形的两条边长分别是6和
8,另一个与它相似的直角三角形的边长分别
是3和4及x,那么x的值
A.只有1个
B.可以有2个
C.有2个以上但有限D.有无数个
4.在△ABC和△DEF中,∠C=∠E=90°,AC
3,AB=7,FE=12,DF=28,则△ABC∽
△FDE
如图,在△ABC中,CD⊥AB于点D,AD=8,
CD=6,则当BD
时,△ADC
△CDB,∠ACB=90
d B
(第5题图)
如图,已知AB⊥BD,CD⊥BD,点P在BD
上,要使△ABP∽△PDC,可再添加的一个条
AB AP
件是
PDp(答案不唯一)
(旁
题多)
图,在△ABC中,∠C=B
90°,AC=8,BC=6,D是边
AB的中点,现有
P位
于边AC上,使得△ADP与
△ABC相似,则线段AP的长为4或
4
8.如图,在△ABC中,AC=3,BC=4,AB=5,在
△DEF中,∠F=90°,DF=6,DE=10.求证
△ABC∽△DEF
B
证明:∵在△ABC中,AC=3,BC=4,AB=5
AC2BCZ=AB2
∠C=90°
在Rt△ABC和Rt△DEF中
AC AB 1
DEDE 2
Rt△ ABOrt△DEF,即△ABC∽△DEF
9.如图,在△ABC中,AC=8cm,BC=6cm
AB=10cm,D是AB上一点,AD=4cm
DE⊥AB交AC于点E,当AE的长为多少
时,△ADE与△ABC相似
解:∵AC=8cm,BC=6cm,
AB-10 cm
AC2BC2=AB2
E
∠C=90°
又∵DE⊥AB,
∠ADE=90°
AD AE
AC AB
4 AE
即当
时,△ADE∽△ACB
当AE=5cm时,△ADE∽△ACB
