【沪科版】数学九年级上册 22.2 相似三角形的判定 第4课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 22.2 相似三角形的判定 第4课时 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览







文档简介
(共20张PPT)
课前预习
颍习新知
1.如果一个三角形的三条边与另一个三角形的
三条边对应成比例,那么这两个三角形相
似(可简单说成:三边成比例的两个三角
形相似)
2.在△ABC和△ABC中,已知AB=1,AC
1.5,BC=2,AB′=12,AC=8,BC′=16,则
△ABC与△ABC相似.理由是三边
成比例的两个三角形相似
当堂训练
巩固基础
知识点三边成比例的两个三角形相似
1.已知△ABC的三边长分别是2,5,6,若要使
△DEF∽△ABC,则△DEF的三边长可以为
A.3,6,7
B.6,15,18
D.10,12,8
2.如果把一个三角形的每条边都扩大为原来的
2倍,那么所得的三角形的每个角
A.都扩大为原来的2倍
B.都扩大为原来的4倍
C.都扩大为原来的6倍
D.都与原来相等
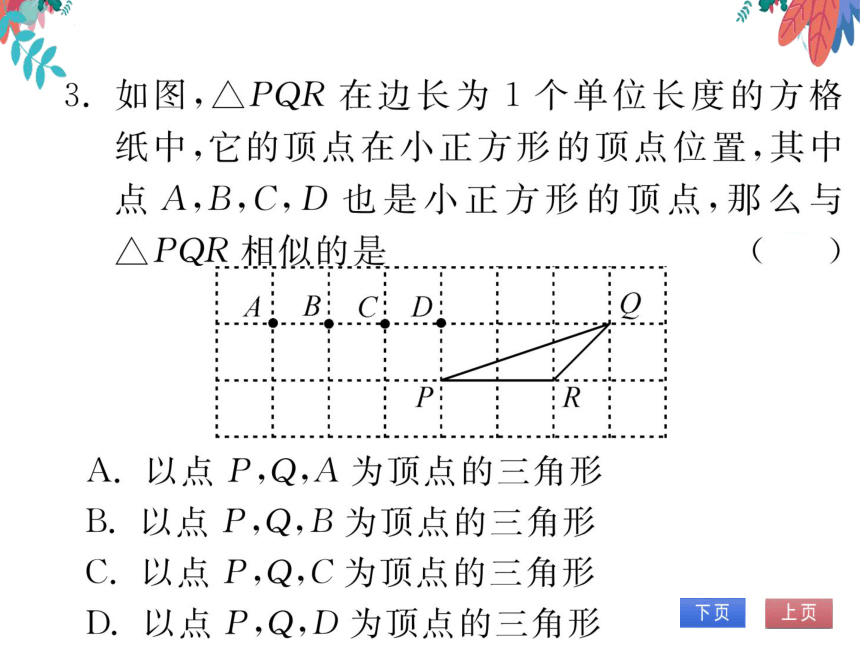
如图,△PQR在边长为1个单位长度的方格
纸中,它的顶点在小正方形的顶点位置,其中
点A,B,C,D也是小正方形的顶点,那么与
△PQR相似的是
B
A.以点P,Q,A为顶点的三角形
B.以点P,Q,B为顶点的三角形
C.以点P,Q,C为顶点的三角形
D.以点P,Q,D为顶点的三角形
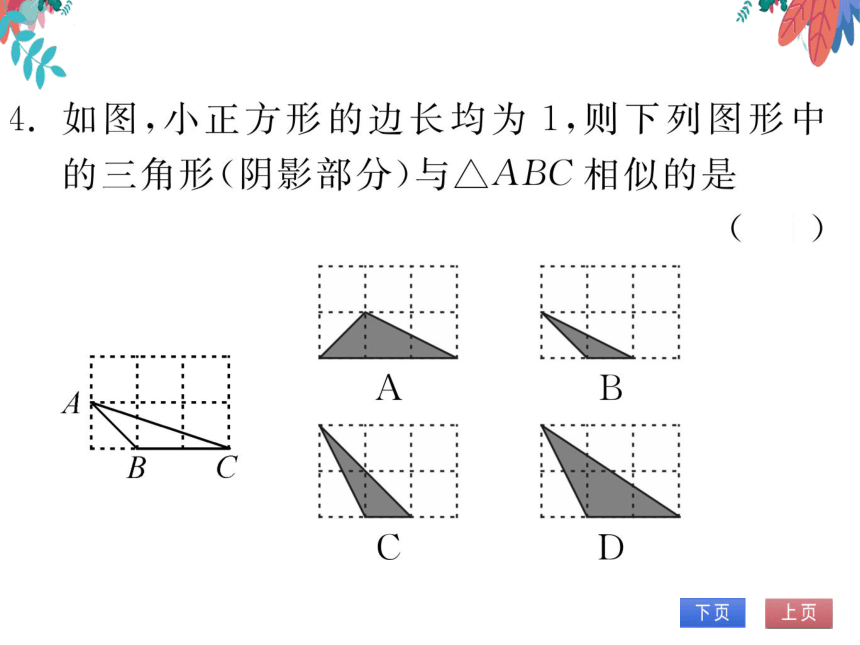
4.如图,小正方形的边长均为1,则下列图形中
的三角形(阴影部分)与△ABC相似的是
B
B
6.已知在△ABC中,AB=√2,AC=√6,BC=2
在△A'BC中,A'B′=1,AC=√3
(1)当∠A满足什么条件时,△ABC∽△ABC
(2)当BC的长为多少时,△ABC△ABC
解:(1)AB
A
ABAC
当∠A=∠A时,△ABCO△ABC
AB AC
(2)
ABAC
BC
时
B
ABCO△ABC
如图,网格图中每个方格都是边长为1的正方
形,若A,B,C,D,E,F都是格点,求证:
△ABC∽ADEF
E
B
证明:由题意知,AB=4
Ac
+1
BC
+1
DE=8,DF=√22+
EF=√62+22=2√1
AB BC CA 1
DE EF FD 2
AbCe
DEF
课后作业
全面提升
1.△ABC的三边长分别为√6,√30和2√3,
ABC的两边长分别为1和5,要使△ABC
△AB′,则△ABC的第三条边长应是(B)
D.2√2
2.如图,在8×4的矩形网格中,每个小正方形的
边长都是1,若△ABC的三个顶点在图中相应
的格点上,图中点D,E,F也都在格点上,则与
△ABC相似的三角形是
A.△ACD
B.△ADF
BDE
CDE
课前预习
颍习新知
1.如果一个三角形的三条边与另一个三角形的
三条边对应成比例,那么这两个三角形相
似(可简单说成:三边成比例的两个三角
形相似)
2.在△ABC和△ABC中,已知AB=1,AC
1.5,BC=2,AB′=12,AC=8,BC′=16,则
△ABC与△ABC相似.理由是三边
成比例的两个三角形相似
当堂训练
巩固基础
知识点三边成比例的两个三角形相似
1.已知△ABC的三边长分别是2,5,6,若要使
△DEF∽△ABC,则△DEF的三边长可以为
A.3,6,7
B.6,15,18
D.10,12,8
2.如果把一个三角形的每条边都扩大为原来的
2倍,那么所得的三角形的每个角
A.都扩大为原来的2倍
B.都扩大为原来的4倍
C.都扩大为原来的6倍
D.都与原来相等
如图,△PQR在边长为1个单位长度的方格
纸中,它的顶点在小正方形的顶点位置,其中
点A,B,C,D也是小正方形的顶点,那么与
△PQR相似的是
B
A.以点P,Q,A为顶点的三角形
B.以点P,Q,B为顶点的三角形
C.以点P,Q,C为顶点的三角形
D.以点P,Q,D为顶点的三角形
4.如图,小正方形的边长均为1,则下列图形中
的三角形(阴影部分)与△ABC相似的是
B
B
6.已知在△ABC中,AB=√2,AC=√6,BC=2
在△A'BC中,A'B′=1,AC=√3
(1)当∠A满足什么条件时,△ABC∽△ABC
(2)当BC的长为多少时,△ABC△ABC
解:(1)AB
A
ABAC
当∠A=∠A时,△ABCO△ABC
AB AC
(2)
ABAC
BC
时
B
ABCO△ABC
如图,网格图中每个方格都是边长为1的正方
形,若A,B,C,D,E,F都是格点,求证:
△ABC∽ADEF
E
B
证明:由题意知,AB=4
Ac
+1
BC
+1
DE=8,DF=√22+
EF=√62+22=2√1
AB BC CA 1
DE EF FD 2
AbCe
DEF
课后作业
全面提升
1.△ABC的三边长分别为√6,√30和2√3,
ABC的两边长分别为1和5,要使△ABC
△AB′,则△ABC的第三条边长应是(B)
D.2√2
2.如图,在8×4的矩形网格中,每个小正方形的
边长都是1,若△ABC的三个顶点在图中相应
的格点上,图中点D,E,F也都在格点上,则与
△ABC相似的三角形是
A.△ACD
B.△ADF
BDE
CDE
