【沪科版】数学九年级上册 22.2 相似三角形的判定 第2课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 22.2 相似三角形的判定 第2课时 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第2课时相似三角形的判定定理
课前预习
颍习新知
1.如果一个三角形的两个角分别与另一个三角
形的两个角对应相等,那么这两个三角形
相似(可简单说成:两角分别相等的两个
角形相似)
2.在△ABC和△DEF中,已知∠A=∠D,
∠B=∠E,则△ABC△DEF
当堂训练
巩固基础
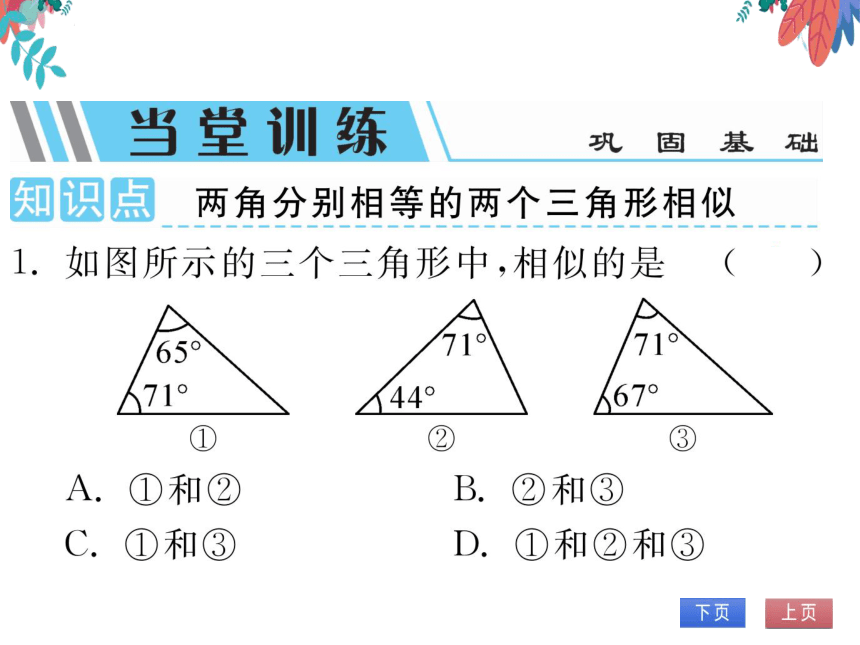
知识点两角分别相等的两个三角形相似
1.如图所示的三个三角形中,相似的是
65°
71°
44°
67°
A.①和②
B.②和③
C.①和③
D.①和②和③
下列各组图形中有可能不相似的是(A
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
图,在矩形ABCD中,E,F分别是CD,BC
上的点,若∠AEF=90°,则一定有(A
A.△ADE∽△ECFB.△ECF∽△AEF
ADE∽△AEFD
AEF∽AABF
D E
B
(第3题图)
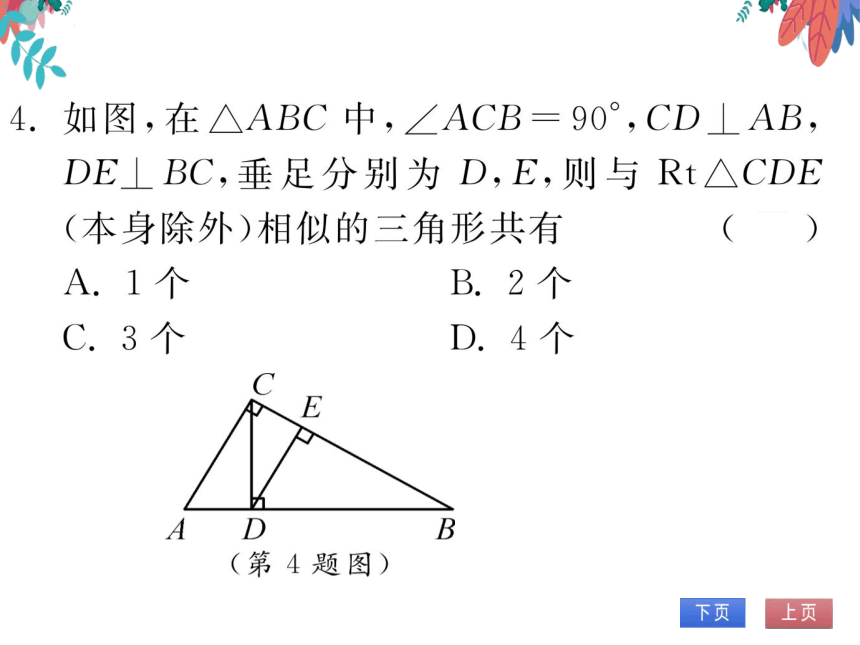
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,
DE⊥BC,垂足分别为D,E,则与Rt△CDE
(本身除外)相似的三角形共有
B.2个
D.4个
E
A D
(第4题图)
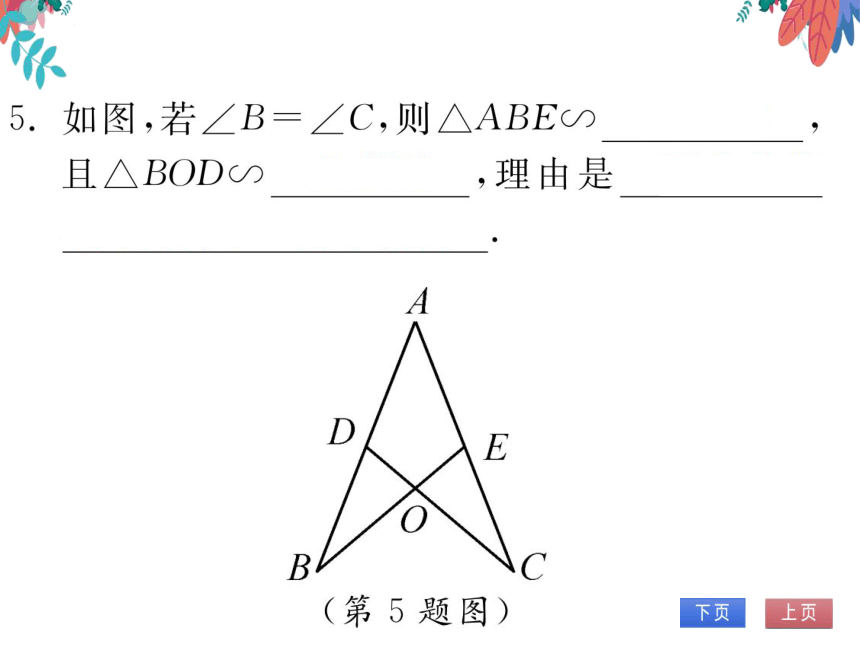
5.如图,若∠B=∠C,则△ABE∽△ACD,
且△BOD∽△COE,理由是两角分别
相等的两个三角形相似
D
B
(第5题图)
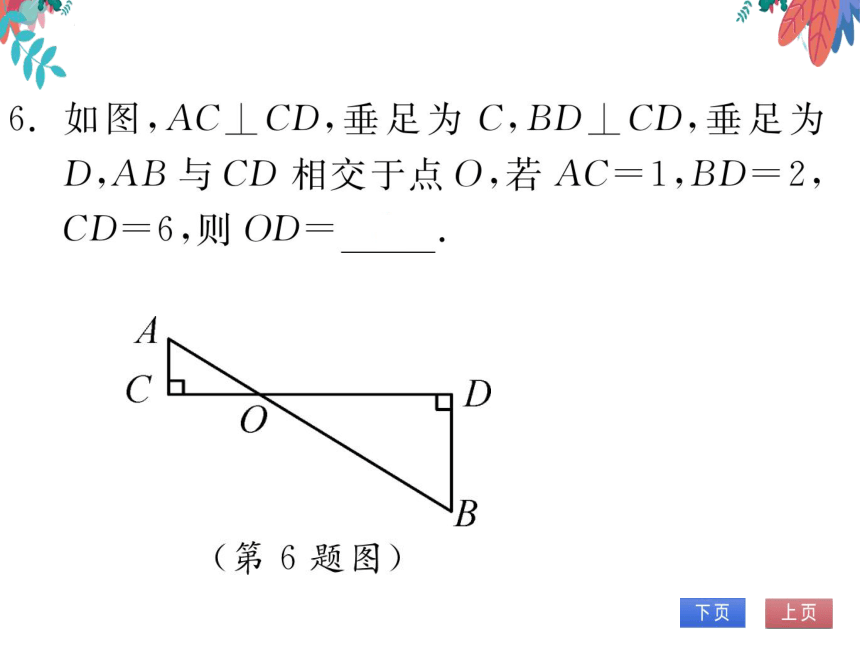
图,AC⊥CD,垂足为C,BD⊥CD,垂足为
D,AB与CD相交于点O,若AC=1,BD
CD=6,则OD
4
D
第6题图
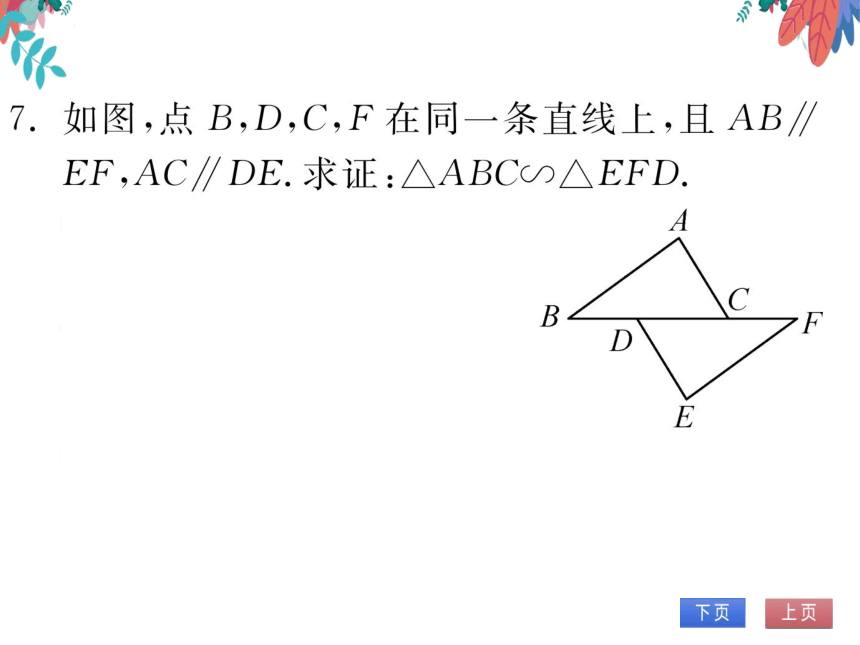
图,点B,D,C,F在同一条直线上,且AB
EF,AC∥DE.求证:△ABC∽△EFD
证明:AB∥EF,
∠B=∠F.
B
C
AC∥DE,
∠ACB=∠EDF.
E
ABC△EFD.
8.如图,在△ABC中,D,E分别是AB,AC上的
点,且∠AED=∠B.若AE=5,AB=9
CB=6,求DE的长
解:∴∠AED=∠B
A=∠A,
△AED△ABC
E
AE DE
AB BO
Ae-5AB=9.cB-6. B
5 DE
DE
9.如图,AD平分∠BAC交BC于点E,连接BD,若
D=∠C求证:AB·AC=AD·AE
证明:∵AD平分∠BAC,
∠BAE=∠CAE
B
E
△ABD△AEC
AB AD
D
AE AC
即AB·AC=AD·AE.
课后作业
全面提升
(枣庄)如图,在Rt△ABC中,∠ACB=90°,
CD⊥AB,垂足为D,AF平分∠CAB,交CD
于点E,交CB于点F,若AC=3,AB=5,则
CE的长为
A
4
D
第2课时相似三角形的判定定理
课前预习
颍习新知
1.如果一个三角形的两个角分别与另一个三角
形的两个角对应相等,那么这两个三角形
相似(可简单说成:两角分别相等的两个
角形相似)
2.在△ABC和△DEF中,已知∠A=∠D,
∠B=∠E,则△ABC△DEF
当堂训练
巩固基础
知识点两角分别相等的两个三角形相似
1.如图所示的三个三角形中,相似的是
65°
71°
44°
67°
A.①和②
B.②和③
C.①和③
D.①和②和③
下列各组图形中有可能不相似的是(A
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
图,在矩形ABCD中,E,F分别是CD,BC
上的点,若∠AEF=90°,则一定有(A
A.△ADE∽△ECFB.△ECF∽△AEF
ADE∽△AEFD
AEF∽AABF
D E
B
(第3题图)
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,
DE⊥BC,垂足分别为D,E,则与Rt△CDE
(本身除外)相似的三角形共有
B.2个
D.4个
E
A D
(第4题图)
5.如图,若∠B=∠C,则△ABE∽△ACD,
且△BOD∽△COE,理由是两角分别
相等的两个三角形相似
D
B
(第5题图)
图,AC⊥CD,垂足为C,BD⊥CD,垂足为
D,AB与CD相交于点O,若AC=1,BD
CD=6,则OD
4
D
第6题图
图,点B,D,C,F在同一条直线上,且AB
EF,AC∥DE.求证:△ABC∽△EFD
证明:AB∥EF,
∠B=∠F.
B
C
AC∥DE,
∠ACB=∠EDF.
E
ABC△EFD.
8.如图,在△ABC中,D,E分别是AB,AC上的
点,且∠AED=∠B.若AE=5,AB=9
CB=6,求DE的长
解:∴∠AED=∠B
A=∠A,
△AED△ABC
E
AE DE
AB BO
Ae-5AB=9.cB-6. B
5 DE
DE
9.如图,AD平分∠BAC交BC于点E,连接BD,若
D=∠C求证:AB·AC=AD·AE
证明:∵AD平分∠BAC,
∠BAE=∠CAE
B
E
△ABD△AEC
AB AD
D
AE AC
即AB·AC=AD·AE.
课后作业
全面提升
(枣庄)如图,在Rt△ABC中,∠ACB=90°,
CD⊥AB,垂足为D,AF平分∠CAB,交CD
于点E,交CB于点F,若AC=3,AB=5,则
CE的长为
A
4
D
