【沪科版】数学九年级上册 22.5 综合与实践 测量与误差 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 22.5 综合与实践 测量与误差 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览






文档简介
(共21张PPT)
课前预习
预习新知
利用影长测量物体的高度,通常利用“相似三
角形对应边成比例”的原理来解决.在同
时刻、同一地点,太阳光下物高的比与影长
的比相等
2.测量河宽、管状物体的内径时,可以构造两个相
似三角形,借助相似三角形的对应边的比相
等来求解
堂训练
巩固基础
知识点1测量高度
1.(临沂)如图,利用标杆BE测量建筑物的高
度,已知标杆高1.2m,测得AB=1.6m
BC=12.4m,则建筑物CD的高度是(B
B.10.5
D.14
B
(第1题图
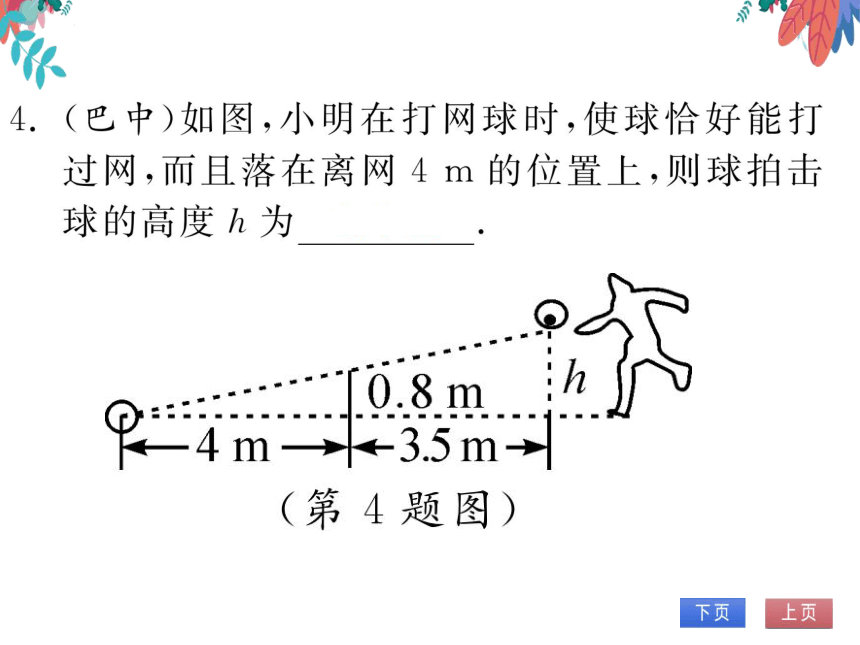
如图,小明在地面上放一面平面镜,选择合适
的位置,刚好在平面镜中看到旗杆的顶部,此
时小明与平面镜的水平距离为2m,旗杆底部
与平面镜的水平距离为16m.若小明的眼睛
与地面的距离为1.5m,则旗杆的高度为
64
12 m D
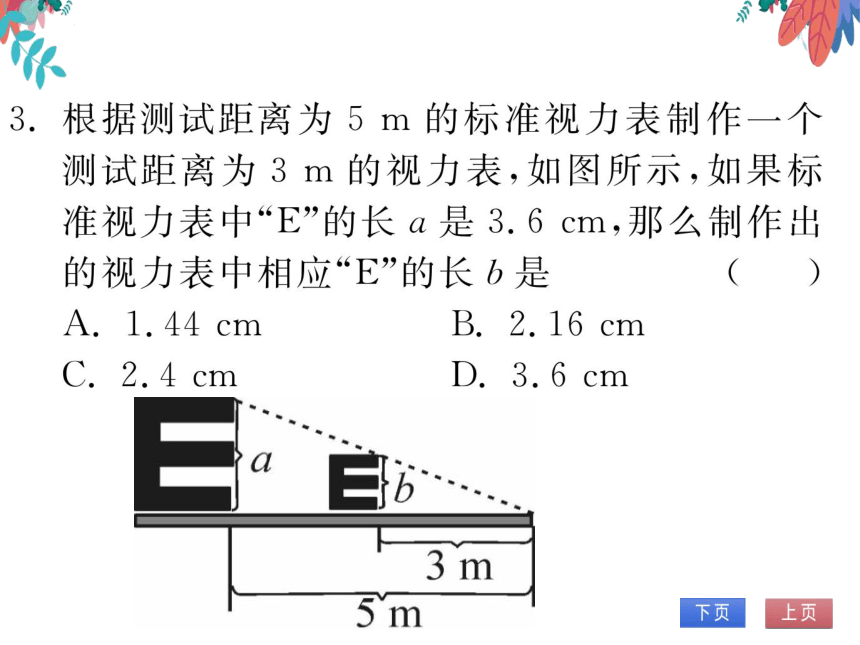
根据测试距离为5m的标准视力表制作
测试距离为3m的视力表,如图所示,如果标
准视力表中“E”的长a是3.6cm,那么制作出
的视力表中相应“E”的长b是
B
A.1.44cm
B.2.16cm
cm
cm
b
3 m
m
(第3题图
地面保持平行,并使边DE与旗杆顶点A在同
直线上,已知DE=0.5m,EF=0.25m,目
测点D到地面的距离DG=1.5m,到旗杆的
水平距离DC=20m,求旗杆AB的高度
DE EF
解:由题意,得△DEF∽△DCA,则
DC CA
DE=0.5m,EF=0.25m,DG=1.5m,
DC-20 m
0.25
20 AC
解得AC=10m
故AB=AC+BC=10+1.5=11.5(m)
答:旗杆AB的高度为11.5m
知识点2测量距离
6.(北京)如图,为估算某河的宽度,在河对岸边
选定一个目标点A,在近岸取点B,C,D,使得
AB⊥BC,CD⊥BC,点E在BC上,并且点A
E,D在同一条直线上.若测得BE=20m
EC=10m,CD=20m,则河的宽度AB等于
B.40
30n
D.20
BE、C
第6题图
图,为了测量一池塘的宽DE,在岸边找到
点C,测得CD=30m,在DC的延长线上找
点A,测得AC=5m,过点A作AB∥DE交
EC的延长线于点B,测出AB=6m,则池塘的
宽DE为
B.30
E∈
B
(第7题图
如图,已知零件的外径为25mm,DC
现用一个交叉卡钳(两条尺长AC
和BD相等,OC=OD)量零件的
内孔直径AB.若OC:OA=1:2,4B
量得CD=10mm,则零件的厚度
mm。
25
课前预习
预习新知
利用影长测量物体的高度,通常利用“相似三
角形对应边成比例”的原理来解决.在同
时刻、同一地点,太阳光下物高的比与影长
的比相等
2.测量河宽、管状物体的内径时,可以构造两个相
似三角形,借助相似三角形的对应边的比相
等来求解
堂训练
巩固基础
知识点1测量高度
1.(临沂)如图,利用标杆BE测量建筑物的高
度,已知标杆高1.2m,测得AB=1.6m
BC=12.4m,则建筑物CD的高度是(B
B.10.5
D.14
B
(第1题图
如图,小明在地面上放一面平面镜,选择合适
的位置,刚好在平面镜中看到旗杆的顶部,此
时小明与平面镜的水平距离为2m,旗杆底部
与平面镜的水平距离为16m.若小明的眼睛
与地面的距离为1.5m,则旗杆的高度为
64
12 m D
根据测试距离为5m的标准视力表制作
测试距离为3m的视力表,如图所示,如果标
准视力表中“E”的长a是3.6cm,那么制作出
的视力表中相应“E”的长b是
B
A.1.44cm
B.2.16cm
cm
cm
b
3 m
m
(第3题图
地面保持平行,并使边DE与旗杆顶点A在同
直线上,已知DE=0.5m,EF=0.25m,目
测点D到地面的距离DG=1.5m,到旗杆的
水平距离DC=20m,求旗杆AB的高度
DE EF
解:由题意,得△DEF∽△DCA,则
DC CA
DE=0.5m,EF=0.25m,DG=1.5m,
DC-20 m
0.25
20 AC
解得AC=10m
故AB=AC+BC=10+1.5=11.5(m)
答:旗杆AB的高度为11.5m
知识点2测量距离
6.(北京)如图,为估算某河的宽度,在河对岸边
选定一个目标点A,在近岸取点B,C,D,使得
AB⊥BC,CD⊥BC,点E在BC上,并且点A
E,D在同一条直线上.若测得BE=20m
EC=10m,CD=20m,则河的宽度AB等于
B.40
30n
D.20
BE、C
第6题图
图,为了测量一池塘的宽DE,在岸边找到
点C,测得CD=30m,在DC的延长线上找
点A,测得AC=5m,过点A作AB∥DE交
EC的延长线于点B,测出AB=6m,则池塘的
宽DE为
B.30
E∈
B
(第7题图
如图,已知零件的外径为25mm,DC
现用一个交叉卡钳(两条尺长AC
和BD相等,OC=OD)量零件的
内孔直径AB.若OC:OA=1:2,4B
量得CD=10mm,则零件的厚度
mm。
25
