鲁教版 数学 九年级上册 3.4 二次函数y=ax2+bx+c的图象与性质课件(共17张PPT)
文档属性
| 名称 | 鲁教版 数学 九年级上册 3.4 二次函数y=ax2+bx+c的图象与性质课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 546.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
二次函数y=ax2+k的图象与性质
4 二次函数y=ax2+bx+c的图象与性质(1)
教学重点:二次函数y=ax2+k的图象和性质.
教学难点:理解抛物线y=ax2与y=ax2+k之间的位置关系.
一、创设情境,导入新课
教学过程
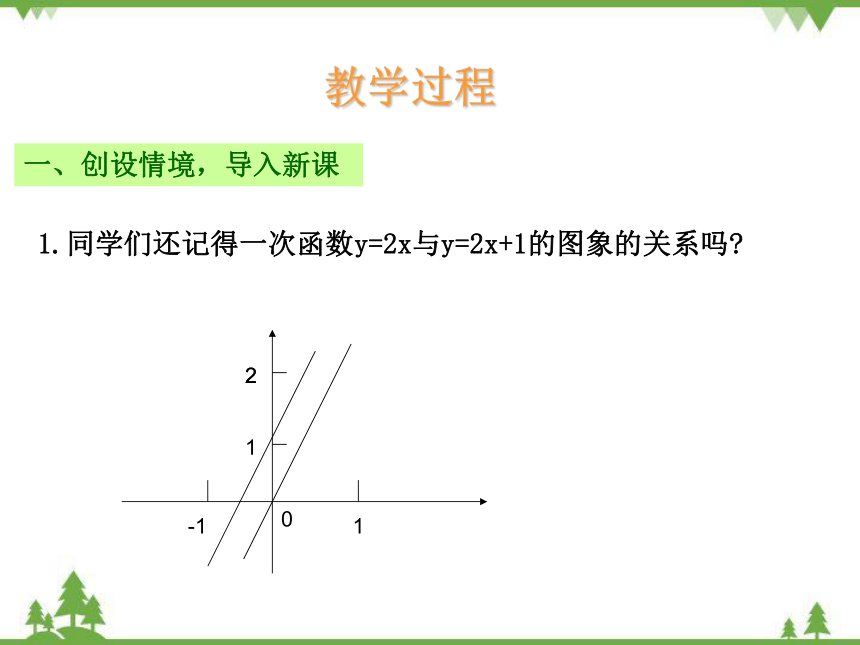
1.同学们还记得一次函数y=2x与y=2x+1的图象的关系吗
2
2
1
-1
1
0
2.你能由此猜想二次函数y=x2与y=x2+1的图象之间的关系吗 ,那么y=x2与y=x2-1的图象之间又有何关系 .
引出课题——y=ax2+k是的图象和性质.
学生观察、思考、回顾回答.
学生猜想、交流,初步了解本节课所要研究的问题.
二、合作探究,感受新知
1.实践例
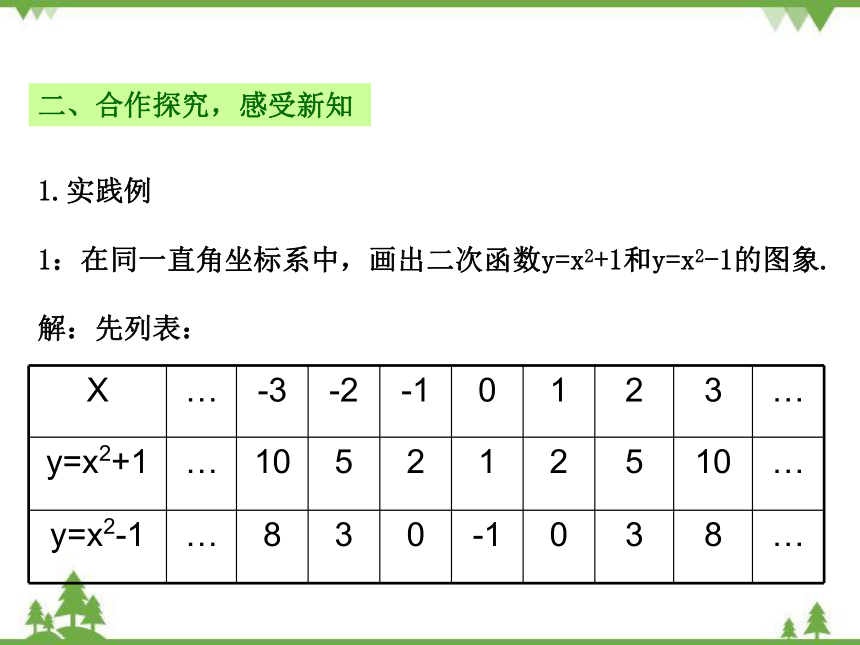
1:在同一直角坐标系中,画出二次函数y=x2+1和y=x2-1的图象.
解:先列表:
X … -3 -2 -1 0 1 2 3 …
y=x2+1 … 10 5 2 1 2 5 10 …
y=x2-1 … 8 3 0 -1 0 3 8 …
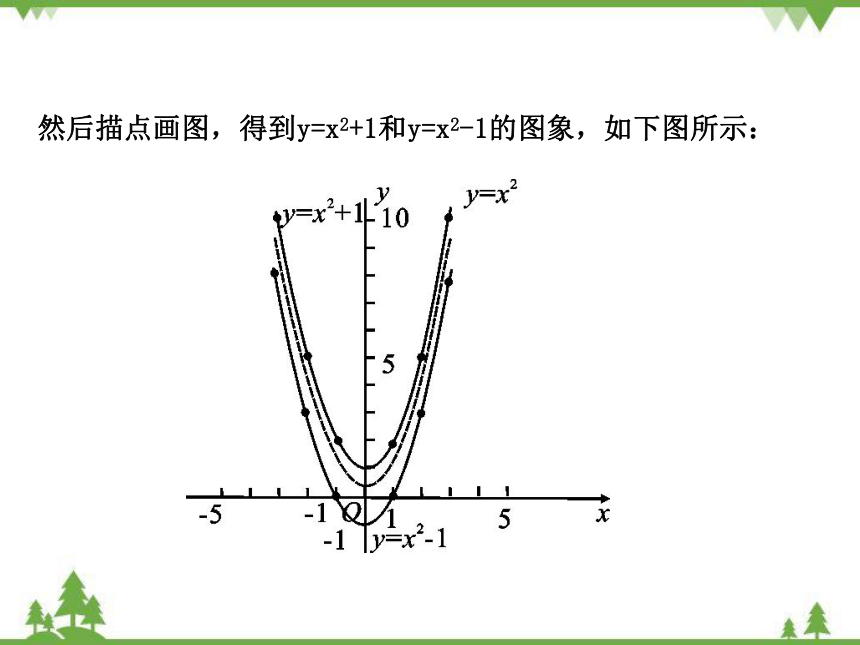
然后描点画图,得到y=x2+1和y=x2-1的图象,如下图所示:
教师课件演示例题中的两个函数图象的画图过程.
教师引导:
1.画图步骤:①列表;②描点;③连线.
2.两个函数可以在一个表格中列出自变量与函数对应值表.
3.两条抛物线也在同一坐标系中画出.
学生课前画出这三条抛物线,课上结合自己的图象仔细观察课件中的图象.
2.思考讨论
(1)抛物线y=x2+1,y=x2-1的开口方向,对称轴,顶点坐标各是什么
(2)抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系
(3)它们的形状由什么决定 它们的位置关系由什么决定
教师先让学生观察自己画出的图象再观看多媒体动画演示.通过图象上下平移,让学生观察总结得出结论.教师引导:两条抛物线的关系,可以从以下几个方面来探究:形状、大小、位置.
抛物线 开口方向 对称轴 定点坐标
y=x2 向上 y轴 (0,0)
y=x2+1 向上 y轴 (0,1)
y=x2-1 向上 y轴 (0,-1)
结论:①
学生仔细观察、大胆猜想、细致总结,小组交流.
②三条抛物线的形状大小完全一样,抛物线y=x2向上平移1个单位就可得到抛物线y=x2+1,向下平移1个单位就可得到抛物线y=x2-1.
③抛物线y=x2、y=x2+1、y=x2-1形状由二次项系数决定,图象的位置由常数项+1、-1决定.
教师适时引导、点拨:仔细观察平移过程,你发现了二次函数y=x2、y=x2+1、y=x2-1图象的大小、形状有什么规律 它们之间位置有什么规律?
教师补充完善.
3.思考
把抛物线y=2x2向上平移5个单位,会得到哪条抛物线 向下平移3、4个单位呢 由此,你会得出怎样的猜想 把你的想法说给同学听听.
小结:(1)一般地,把抛物线y=ax2向上平移k(k>0)个单位,就得到抛物线y=ax2+k;把抛物线y=ax2向下平移k(k>0)个单位,就得到抛物线y=ax2-k.
(2)抛物线y=x2+1与y=x2-1可以经过怎样的相互平移得到
教师引导学生画图、观察、思考、归纳总结得出结论.
教师点拨:抛物线y=x2+1沿y轴向下平移1个单位得到抛物线y=x2,再向下平移1个单位就得到抛物线y=x2-1;反之y=x2-1也可以向上平移得到抛物线y=x2+1.
学生类比观察、归纳总结,小组交流得出结论.
4.应用
例2(补充):在同一直角坐标系中,画出函数y=-x2+1与y=-x2-1的图象,并说明,通过怎样的平移,可以由抛物线y=-x2+1得到抛物线y=-x2-1,指出它们的开口方向、对称轴、顶点坐标.
解:列表
x … -3 -2 -1 0 1 2 3 …
y=-x2+1 … -8 -3 0 1 0 -3 -8 …
y=-x2-1 … -10 -5 -2 -1 -2 -5 -10 …
描点、连线,画出这两个函数的图象.
可以看出,抛物线y=-x2-1是由抛物线y=-x2+1向下平移两个单位得到的.y=-x2-1的开口方向:向下,对称轴:y轴,顶点坐标(0,-1);y=-x2+1开口方向:向下,对称轴:y轴,顶点坐标(0,1).
教师引导:例2中的两个函数图象与例1中的图象相比,开口方向不同,平移规律不变.
学生独立解决后,与同伴交流看法.
小结:抛物线y=ax2+k(k>0)向下平移2k个单位就可得到抛物线y=ax2-k(k>0);抛物线y=ax2-k(k>0)向上平移2k个单位就可得到抛物线y=ax2+k(k>0).
抛物线y=ax2+k开口方向由a的符号决定(a>0,开口向上,a<0,开口向下),对称轴都是y轴,顶点坐标(0,k).
教师引导学生得到平移规律.y=ax2+k型的二次函数图象平移由k决定,k由小变大,则向上平移,反之,向下平移,平移的距离是大k与小k的差.
三、课堂小结,梳理新知
师生小结
(1)通过本节课的学习,你有哪些收获
从二次函数y=ax2+k的图象形状、画法、对称轴、顶点、开口方向和大小等方面去总结.
(2)你对本节课有什么疑惑 说给老师或同学听听.师生共同回顾总结,归纳本节所学的知识.
教师聆听同学的收获的同时,认真解决同学的疑惑,教师补充完善.
学生归纳、总结自由发言,学生体会、反思.
二次函数y=ax2+k的图象与性质
4 二次函数y=ax2+bx+c的图象与性质(1)
教学重点:二次函数y=ax2+k的图象和性质.
教学难点:理解抛物线y=ax2与y=ax2+k之间的位置关系.
一、创设情境,导入新课
教学过程
1.同学们还记得一次函数y=2x与y=2x+1的图象的关系吗
2
2
1
-1
1
0
2.你能由此猜想二次函数y=x2与y=x2+1的图象之间的关系吗 ,那么y=x2与y=x2-1的图象之间又有何关系 .
引出课题——y=ax2+k是的图象和性质.
学生观察、思考、回顾回答.
学生猜想、交流,初步了解本节课所要研究的问题.
二、合作探究,感受新知
1.实践例
1:在同一直角坐标系中,画出二次函数y=x2+1和y=x2-1的图象.
解:先列表:
X … -3 -2 -1 0 1 2 3 …
y=x2+1 … 10 5 2 1 2 5 10 …
y=x2-1 … 8 3 0 -1 0 3 8 …
然后描点画图,得到y=x2+1和y=x2-1的图象,如下图所示:
教师课件演示例题中的两个函数图象的画图过程.
教师引导:
1.画图步骤:①列表;②描点;③连线.
2.两个函数可以在一个表格中列出自变量与函数对应值表.
3.两条抛物线也在同一坐标系中画出.
学生课前画出这三条抛物线,课上结合自己的图象仔细观察课件中的图象.
2.思考讨论
(1)抛物线y=x2+1,y=x2-1的开口方向,对称轴,顶点坐标各是什么
(2)抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系
(3)它们的形状由什么决定 它们的位置关系由什么决定
教师先让学生观察自己画出的图象再观看多媒体动画演示.通过图象上下平移,让学生观察总结得出结论.教师引导:两条抛物线的关系,可以从以下几个方面来探究:形状、大小、位置.
抛物线 开口方向 对称轴 定点坐标
y=x2 向上 y轴 (0,0)
y=x2+1 向上 y轴 (0,1)
y=x2-1 向上 y轴 (0,-1)
结论:①
学生仔细观察、大胆猜想、细致总结,小组交流.
②三条抛物线的形状大小完全一样,抛物线y=x2向上平移1个单位就可得到抛物线y=x2+1,向下平移1个单位就可得到抛物线y=x2-1.
③抛物线y=x2、y=x2+1、y=x2-1形状由二次项系数决定,图象的位置由常数项+1、-1决定.
教师适时引导、点拨:仔细观察平移过程,你发现了二次函数y=x2、y=x2+1、y=x2-1图象的大小、形状有什么规律 它们之间位置有什么规律?
教师补充完善.
3.思考
把抛物线y=2x2向上平移5个单位,会得到哪条抛物线 向下平移3、4个单位呢 由此,你会得出怎样的猜想 把你的想法说给同学听听.
小结:(1)一般地,把抛物线y=ax2向上平移k(k>0)个单位,就得到抛物线y=ax2+k;把抛物线y=ax2向下平移k(k>0)个单位,就得到抛物线y=ax2-k.
(2)抛物线y=x2+1与y=x2-1可以经过怎样的相互平移得到
教师引导学生画图、观察、思考、归纳总结得出结论.
教师点拨:抛物线y=x2+1沿y轴向下平移1个单位得到抛物线y=x2,再向下平移1个单位就得到抛物线y=x2-1;反之y=x2-1也可以向上平移得到抛物线y=x2+1.
学生类比观察、归纳总结,小组交流得出结论.
4.应用
例2(补充):在同一直角坐标系中,画出函数y=-x2+1与y=-x2-1的图象,并说明,通过怎样的平移,可以由抛物线y=-x2+1得到抛物线y=-x2-1,指出它们的开口方向、对称轴、顶点坐标.
解:列表
x … -3 -2 -1 0 1 2 3 …
y=-x2+1 … -8 -3 0 1 0 -3 -8 …
y=-x2-1 … -10 -5 -2 -1 -2 -5 -10 …
描点、连线,画出这两个函数的图象.
可以看出,抛物线y=-x2-1是由抛物线y=-x2+1向下平移两个单位得到的.y=-x2-1的开口方向:向下,对称轴:y轴,顶点坐标(0,-1);y=-x2+1开口方向:向下,对称轴:y轴,顶点坐标(0,1).
教师引导:例2中的两个函数图象与例1中的图象相比,开口方向不同,平移规律不变.
学生独立解决后,与同伴交流看法.
小结:抛物线y=ax2+k(k>0)向下平移2k个单位就可得到抛物线y=ax2-k(k>0);抛物线y=ax2-k(k>0)向上平移2k个单位就可得到抛物线y=ax2+k(k>0).
抛物线y=ax2+k开口方向由a的符号决定(a>0,开口向上,a<0,开口向下),对称轴都是y轴,顶点坐标(0,k).
教师引导学生得到平移规律.y=ax2+k型的二次函数图象平移由k决定,k由小变大,则向上平移,反之,向下平移,平移的距离是大k与小k的差.
三、课堂小结,梳理新知
师生小结
(1)通过本节课的学习,你有哪些收获
从二次函数y=ax2+k的图象形状、画法、对称轴、顶点、开口方向和大小等方面去总结.
(2)你对本节课有什么疑惑 说给老师或同学听听.师生共同回顾总结,归纳本节所学的知识.
教师聆听同学的收获的同时,认真解决同学的疑惑,教师补充完善.
学生归纳、总结自由发言,学生体会、反思.
