青岛版数学九年级上册 3.3圆周角(2) 课件(共16张PPT)
文档属性
| 名称 | 青岛版数学九年级上册 3.3圆周角(2) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 402.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
3.3圆周角(2)
学习目标
1.了解同弧上圆周角的关系.
2.了解直径所对的圆周角的度数.
复习引入
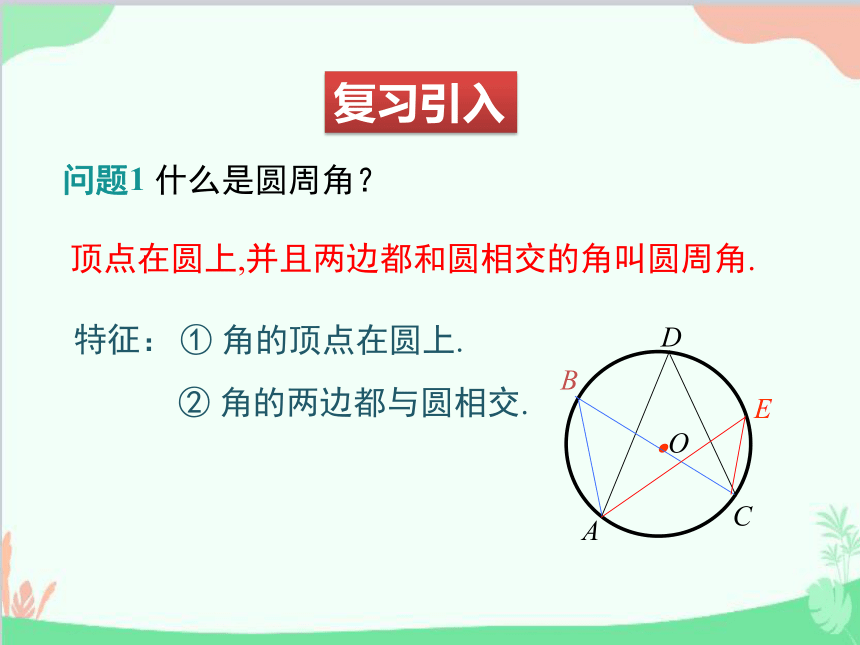
问题1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
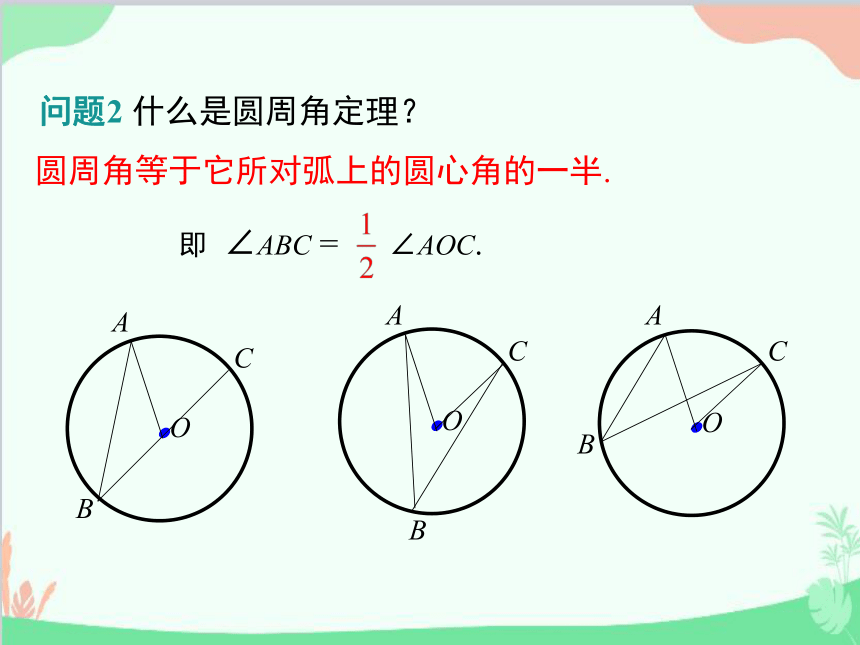
问题2 什么是圆周角定理?
圆周角等于它所对弧上的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
讲授新课
圆周角定理的推论2
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
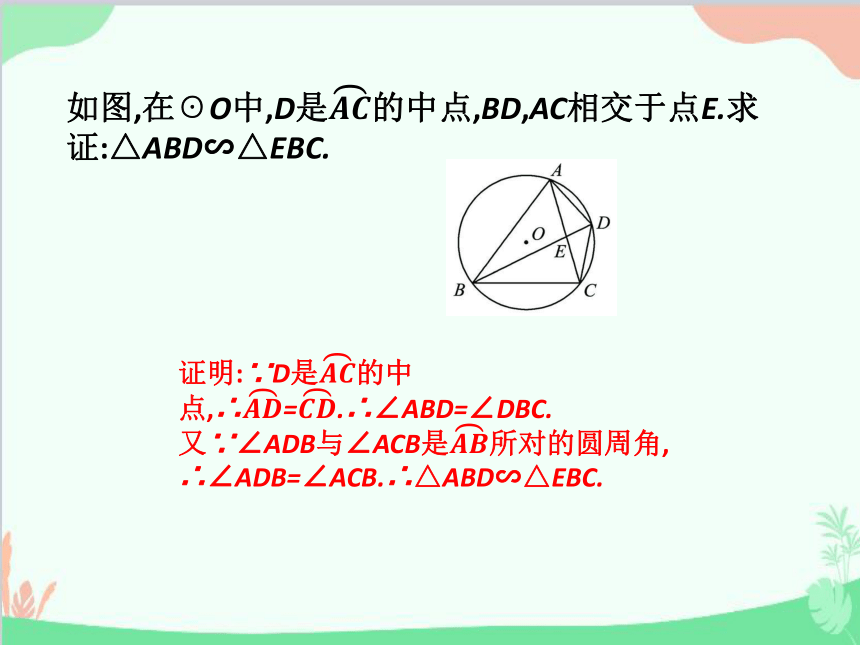
如图,在☉O中,D是的中点,BD,AC相交于点E.求证:△ABD∽△EBC.
证明:∵D是的中点,∴=.∴∠ABD=∠DBC.
又∵∠ADB与∠ACB是所对的圆周角,
∴∠ADB=∠ACB.∴△ABD∽△EBC.
直径所对应的圆周角
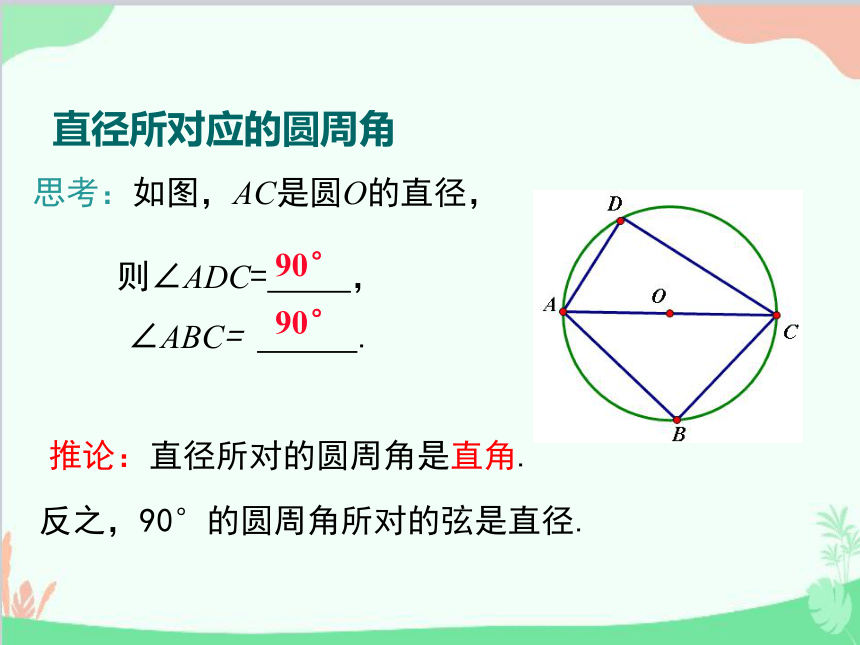
思考:如图,AC是圆O的直径,
则∠ADC= ,
∠ABC= .
90°
90°
推论:直径所对的圆周角是直角.
反之,90°的圆周角所对的弦是直径.
问题 你能确定圆形笑脸的圆心吗?
利用三角板在圆中画出两个90°的圆周角,这样就得到
两条直径,那么这两条直径的交点就是圆心.
如图,⊙O的直径AC为10 cm,弦AD为6 cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB,BC的长.
B
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
在Rt△ABC中,AB2+BC2=AC2,
(2)∵ AC是直径,∴ ∠ABC=90°.
∵BD平∠ADC,∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳
如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.
C
练一练
1.如图,AB是⊙O的直径, C ,D是圆上的两点,∠ABD=40°,则∠BCD=____.
50°
A
B
O
C
D
2.如图,∠A=50°, ∠ABC=60 °,BD是⊙O的直径,则∠AEB等于 ( )
A.70° B.110°
C.90° D.120°
B
A
C
B
O
D
E
随堂练习
3.如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
A.3 B. C. D.2
A
4.如图,点A,B,D,E在⊙O上,弦AE,BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB,AC之间的大小关系,并给出证明.
解:(1)AB=AC.
证明如下:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°, 即AD⊥BC.
∵BD=DC,
∴AD垂直平分BC,
∴AB=AC.
(2)在上述题设条件下,当△ABC为正三角形时,点E是否为AC的中点?为什么?
(2)当△ABC为正三角形时,E是AC的中点.
理由如下:连接BE,
∵AB为⊙O的直径,
∴∠BEA=90°,即BE⊥AC.
∵△ABC为正三角形,
∴AE=EC,
即E是AC的中点.
圆周角定理
推论2
推论3
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径
课堂小结
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
3.3圆周角(2)
学习目标
1.了解同弧上圆周角的关系.
2.了解直径所对的圆周角的度数.
复习引入
问题1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
问题2 什么是圆周角定理?
圆周角等于它所对弧上的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
讲授新课
圆周角定理的推论2
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
如图,在☉O中,D是的中点,BD,AC相交于点E.求证:△ABD∽△EBC.
证明:∵D是的中点,∴=.∴∠ABD=∠DBC.
又∵∠ADB与∠ACB是所对的圆周角,
∴∠ADB=∠ACB.∴△ABD∽△EBC.
直径所对应的圆周角
思考:如图,AC是圆O的直径,
则∠ADC= ,
∠ABC= .
90°
90°
推论:直径所对的圆周角是直角.
反之,90°的圆周角所对的弦是直径.
问题 你能确定圆形笑脸的圆心吗?
利用三角板在圆中画出两个90°的圆周角,这样就得到
两条直径,那么这两条直径的交点就是圆心.
如图,⊙O的直径AC为10 cm,弦AD为6 cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB,BC的长.
B
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
在Rt△ABC中,AB2+BC2=AC2,
(2)∵ AC是直径,∴ ∠ABC=90°.
∵BD平∠ADC,∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳
如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.
C
练一练
1.如图,AB是⊙O的直径, C ,D是圆上的两点,∠ABD=40°,则∠BCD=____.
50°
A
B
O
C
D
2.如图,∠A=50°, ∠ABC=60 °,BD是⊙O的直径,则∠AEB等于 ( )
A.70° B.110°
C.90° D.120°
B
A
C
B
O
D
E
随堂练习
3.如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
A.3 B. C. D.2
A
4.如图,点A,B,D,E在⊙O上,弦AE,BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB,AC之间的大小关系,并给出证明.
解:(1)AB=AC.
证明如下:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°, 即AD⊥BC.
∵BD=DC,
∴AD垂直平分BC,
∴AB=AC.
(2)在上述题设条件下,当△ABC为正三角形时,点E是否为AC的中点?为什么?
(2)当△ABC为正三角形时,E是AC的中点.
理由如下:连接BE,
∵AB为⊙O的直径,
∴∠BEA=90°,即BE⊥AC.
∵△ABC为正三角形,
∴AE=EC,
即E是AC的中点.
圆周角定理
推论2
推论3
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径
课堂小结
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
