青岛版数学九年级上册 1.2怎样判定三角形相似(2) 课件(共20张PPT)
文档属性
| 名称 | 青岛版数学九年级上册 1.2怎样判定三角形相似(2) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 253.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 15:30:02 | ||
图片预览




文档简介
(共20张PPT)
1.2怎样判定三角形相似(2)
1.理解相似三角形的定义,掌握定义中的两个条件.
2.掌握相似三角形的判定定理1.(重点)
3.能熟练运用相似三角形的判定定理1.(难点)
学习目标
问题1:这两个三角形有什么关系?
观察与思考
全等三角形
导入新课
那这样变化一下呢?
相似三角形
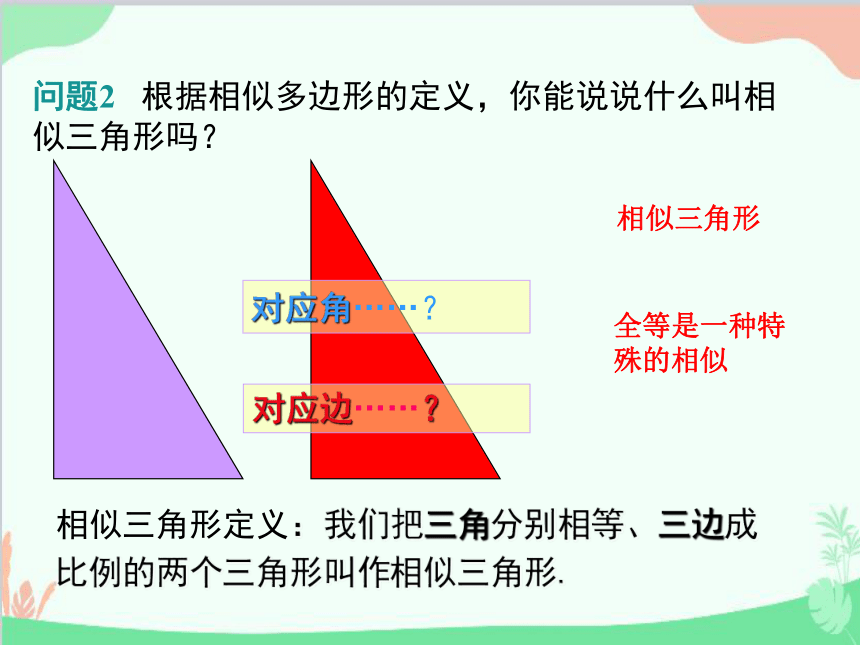
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫作相似三角形.
对应角……?
对应边……?
问题2 根据相似多边形的定义,你能说说什么叫相似三角形吗?
全等是一种特殊的相似
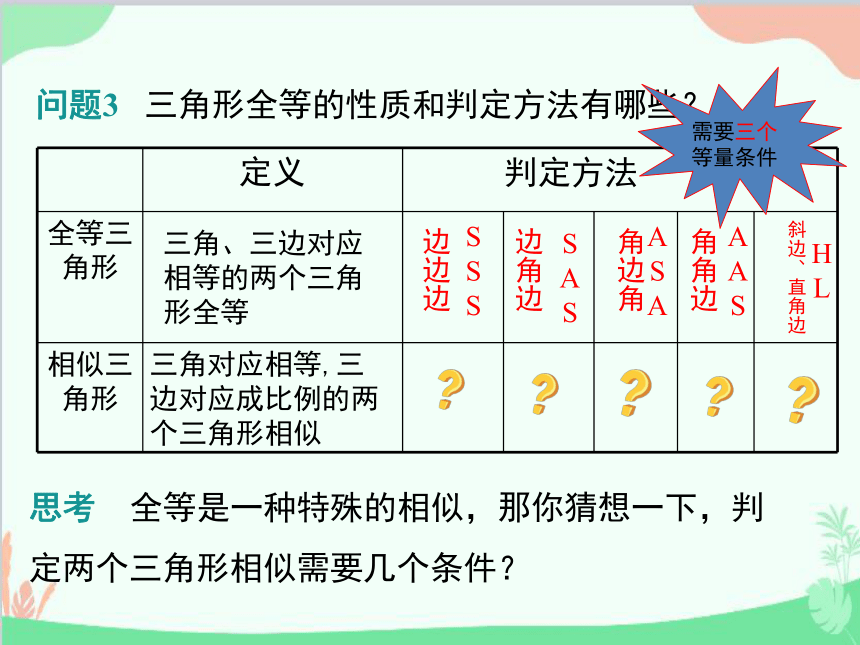
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
学校举办活动,需要三个内角分别为90°,60°,30°的形状相同、大小不同的三角纸板若干. 小明手上的测量工具只有一个量角器,他该怎么做呢?
情境引入
?
?
?
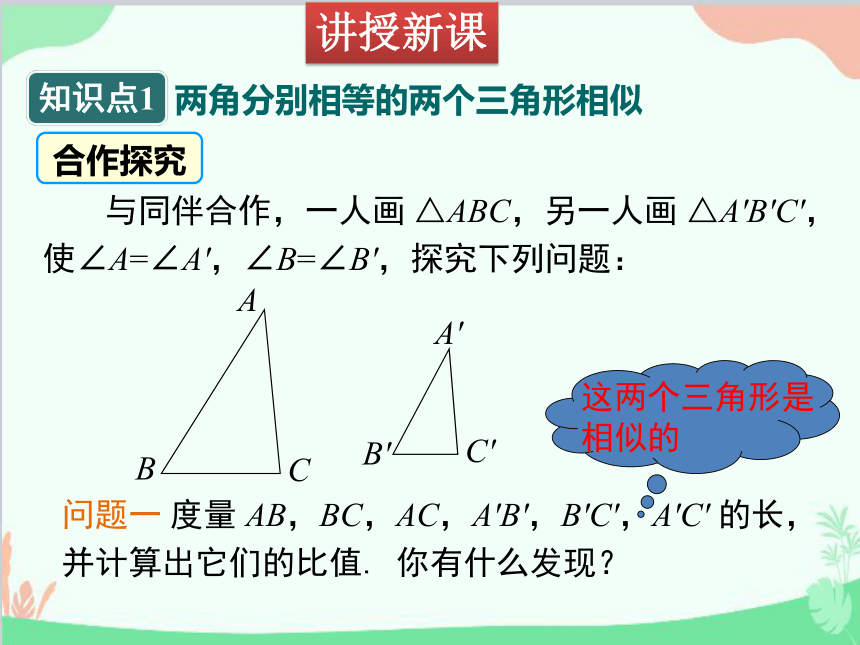
问题一 度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值. 你有什么发现?
C
A
B
A'
B'
C'
合作探究
与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A=∠A′,∠B=∠B′,探究下列问题:
这两个三角形是相似的
讲授新课
两角分别相等的两个三角形相似
知识点1
证明:在 △ABC 的边 AB(或 AB 的延长线)上,
截取 AD=A′B′,过点 D 作 DE // BC,交 AC 于点 E,
则有△ADE ∽△ABC,∠ADE =∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵ AD=A′B′,∠A=∠A′,
∴△ADE ≌△A′B′C′,
∴△A′B′C′ ∽△ABC.
C
A
A'
B
B'
C'
D
E
问题二 试证明△A′B′C′∽△ABC.
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
C
A
B
A'
B'
C'
归纳:
例1:如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC
(两角分别相等的两个三角形相似).
∴
∴BC=14.
B
A
D
E
C
典例精析
如图,△ABC中,DE∥BC,EF∥AB,求证:
△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
练一练
证明:
∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
例2:如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
例3 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有 ( )
A. 1对 B. 2对
C. 3对 D. 4对
C
随堂练习
2. 如图,△ABC中,AE 交 BC 于点 D,∠C=∠E,AD : DE=3 : 5,AE=8,BD=4,则DC的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
A
B
D
C
3. 如图,点 D 在 AB上,当∠ =∠ (或
∠ =∠ )时, △ACD∽△ABC.
ACD
ACB
B
ADB
证明:∵ 在△ ABC中,∠A=40 ° ,
∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△DEF中,∠E=80 °,
∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
4. 如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 ° .求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明: ∵ △ABC 的高AD,BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
5. 如图,△ABC 的高 AD,BE 交于点 F.
求证:
D
C
A
B
E
F
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
课堂小结
1.2怎样判定三角形相似(2)
1.理解相似三角形的定义,掌握定义中的两个条件.
2.掌握相似三角形的判定定理1.(重点)
3.能熟练运用相似三角形的判定定理1.(难点)
学习目标
问题1:这两个三角形有什么关系?
观察与思考
全等三角形
导入新课
那这样变化一下呢?
相似三角形
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫作相似三角形.
对应角……?
对应边……?
问题2 根据相似多边形的定义,你能说说什么叫相似三角形吗?
全等是一种特殊的相似
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
学校举办活动,需要三个内角分别为90°,60°,30°的形状相同、大小不同的三角纸板若干. 小明手上的测量工具只有一个量角器,他该怎么做呢?
情境引入
?
?
?
问题一 度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值. 你有什么发现?
C
A
B
A'
B'
C'
合作探究
与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A=∠A′,∠B=∠B′,探究下列问题:
这两个三角形是相似的
讲授新课
两角分别相等的两个三角形相似
知识点1
证明:在 △ABC 的边 AB(或 AB 的延长线)上,
截取 AD=A′B′,过点 D 作 DE // BC,交 AC 于点 E,
则有△ADE ∽△ABC,∠ADE =∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵ AD=A′B′,∠A=∠A′,
∴△ADE ≌△A′B′C′,
∴△A′B′C′ ∽△ABC.
C
A
A'
B
B'
C'
D
E
问题二 试证明△A′B′C′∽△ABC.
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
C
A
B
A'
B'
C'
归纳:
例1:如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC
(两角分别相等的两个三角形相似).
∴
∴BC=14.
B
A
D
E
C
典例精析
如图,△ABC中,DE∥BC,EF∥AB,求证:
△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
练一练
证明:
∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
例2:如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
例3 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有 ( )
A. 1对 B. 2对
C. 3对 D. 4对
C
随堂练习
2. 如图,△ABC中,AE 交 BC 于点 D,∠C=∠E,AD : DE=3 : 5,AE=8,BD=4,则DC的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
A
B
D
C
3. 如图,点 D 在 AB上,当∠ =∠ (或
∠ =∠ )时, △ACD∽△ABC.
ACD
ACB
B
ADB
证明:∵ 在△ ABC中,∠A=40 ° ,
∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△DEF中,∠E=80 °,
∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
4. 如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 ° .求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明: ∵ △ABC 的高AD,BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
5. 如图,△ABC 的高 AD,BE 交于点 F.
求证:
D
C
A
B
E
F
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
课堂小结
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
