【沪科版】数学九年级上册 23.2 解直角三角形及其应用 第1课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 23.2 解直角三角形及其应用 第1课时 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览







文档简介
(共25张PPT)
23.2解直角三角形及其应用
第1课时解直角三角形
N课前预习
领习新知
1.在直角三角形中,除直角外,由已知元素求出
未知元素的过程,叫做解直角三角形
2.在Rt△ABC中,∠C=90°:
(1)三边a,b,c之间的关系是a2+b2=c;
(2)锐角之间的关系是A+∠B=90°;
(3)边角之间的关系是sinA
cOs
A
b
b
g tan
sin b
C
COS
c tan B
当堂训练
巩固基础
知识点1解直角三角形
在△ABC中,a,b,c分别是∠A,∠B,∠C的
对边,如果a2+b2=c2,那么下列结论正确的
A
a.c sin a=a
b.bcos b=c
a tan a=b
D. c tanb=b
2.如图,在Rt△ABC中,斜边AB的长为m
∠A=35°,则直角边BC的长是
a. msin 35
B.ncos35°
cos
B
A
C
(第2题图)
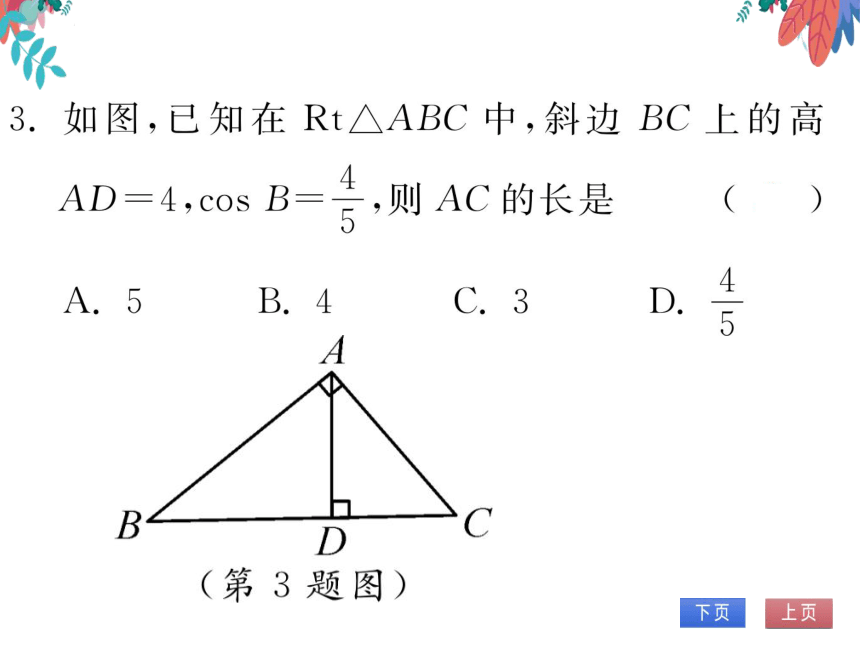
图,已知在Rt△ABC中,斜边BC上的
AD=4, cos B 4
则AC的长是
C.3
D
B
D
C
(第3题图)
4.已知在Rt△ABC中,∠B=60°,斜边AB=1
那么此直角三角形的周长是
3+3
D
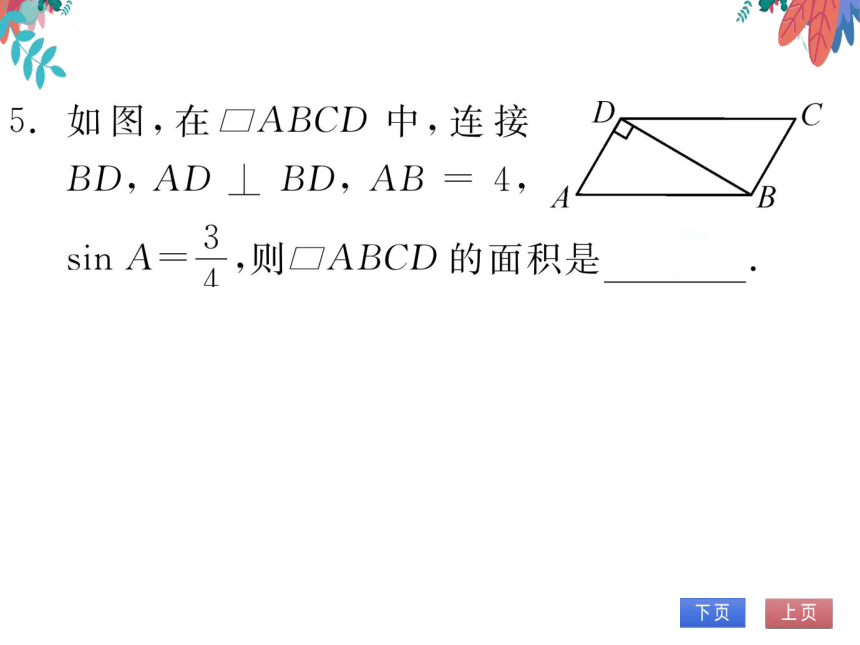
图,在□ABCD中,连接
BD, AD BD, AB= 4
A
B
A=,则ABCD的面积是37
解:(1)在Rt△ABC
C=90°,∠A=30
e sin
3,b=√c2
123
又∵∠A+∠B=90°,∴∠B=60
(2)
24,c=242,∴b
C
24
B=45°
知识点2解斜三角形
7.如图,在△ABC中,cosB
Sin
AC=5,则△ABC的面积是
B
21
C.14
D.21
30°
D
解:过点C作CD⊥AB于
点D,在Rt△ACD中
∠30°545
∠A=30
CD
AC=3.由勾股定理得AD
在Rt△BCD中,tan45°CD
BD1
BD
CD=3.AB-AD+BD=3+3
课后作业
全面提升
1.在下列条件中不能解直角三角形的是(B
A.已知两条边
B.已知两锐角
C.已知一边及一锐角D.已知三边
2.如图,在梯形ABCD中,AD∥BC,AC⊥AB
AD=CD,cos∠DCA=,BC=10,则AB的
长是
B
(第2题图)
3.如图,在矩形ABCD中,DE⊥AC于点E,设
∠ADE=a,且cosa=,AB=4,则AD的长
为
16
20
16
B
第3题图
23.2解直角三角形及其应用
第1课时解直角三角形
N课前预习
领习新知
1.在直角三角形中,除直角外,由已知元素求出
未知元素的过程,叫做解直角三角形
2.在Rt△ABC中,∠C=90°:
(1)三边a,b,c之间的关系是a2+b2=c;
(2)锐角之间的关系是A+∠B=90°;
(3)边角之间的关系是sinA
cOs
A
b
b
g tan
sin b
C
COS
c tan B
当堂训练
巩固基础
知识点1解直角三角形
在△ABC中,a,b,c分别是∠A,∠B,∠C的
对边,如果a2+b2=c2,那么下列结论正确的
A
a.c sin a=a
b.bcos b=c
a tan a=b
D. c tanb=b
2.如图,在Rt△ABC中,斜边AB的长为m
∠A=35°,则直角边BC的长是
a. msin 35
B.ncos35°
cos
B
A
C
(第2题图)
图,已知在Rt△ABC中,斜边BC上的
AD=4, cos B 4
则AC的长是
C.3
D
B
D
C
(第3题图)
4.已知在Rt△ABC中,∠B=60°,斜边AB=1
那么此直角三角形的周长是
3+3
D
图,在□ABCD中,连接
BD, AD BD, AB= 4
A
B
A=,则ABCD的面积是37
解:(1)在Rt△ABC
C=90°,∠A=30
e sin
3,b=√c2
123
又∵∠A+∠B=90°,∴∠B=60
(2)
24,c=242,∴b
C
24
B=45°
知识点2解斜三角形
7.如图,在△ABC中,cosB
Sin
AC=5,则△ABC的面积是
B
21
C.14
D.21
30°
D
解:过点C作CD⊥AB于
点D,在Rt△ACD中
∠30°545
∠A=30
CD
AC=3.由勾股定理得AD
在Rt△BCD中,tan45°CD
BD1
BD
CD=3.AB-AD+BD=3+3
课后作业
全面提升
1.在下列条件中不能解直角三角形的是(B
A.已知两条边
B.已知两锐角
C.已知一边及一锐角D.已知三边
2.如图,在梯形ABCD中,AD∥BC,AC⊥AB
AD=CD,cos∠DCA=,BC=10,则AB的
长是
B
(第2题图)
3.如图,在矩形ABCD中,DE⊥AC于点E,设
∠ADE=a,且cosa=,AB=4,则AD的长
为
16
20
16
B
第3题图
