【沪科版】数学九年级上册 23.2 解直角三角形及其应用 第4课时 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 23.2 解直角三角形及其应用 第4课时 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览







文档简介
(共25张PPT)
课前预习
预习新知
小明爬一土坡,他从A处爬到B处所走的直线
距离AB=4m,此时,他离地面的高度h=2
则这个土坡的坡角∠A=30°;土坡AB的
坡度为1:3
2.P1(x1,y1),P2(x2,y2)是直线y=kx+b(k
0)上的任意两点,这条直线向上方向与x轴正
方向所夹的锐角为α,则tana
k
当堂训练
巩固基础
知识点1坡度、坡角问题
1.一斜坡的坡度为1:3,如果某人站的位置的
水平宽度为6m,则他所在的位置的铅直高度
为
a2 m
B.18
D
2.某水库大坝的横断面是四边形ABDE,AE∥
BD,坝内斜坡的坡度i1=1:3,坝外斜坡的
坡度i2=1:1,则两个坡角的和为
A.90
B.60
D.105
3.如图,防洪大堤的横断面是四边形ABDE
AE∥BD,坝高AC为6m,背水坡AB的坡度
为1:2,则斜坡AB的长为
A.13m
B.6√5m
C.56m
D.14m
6 m
B
(第3题图)
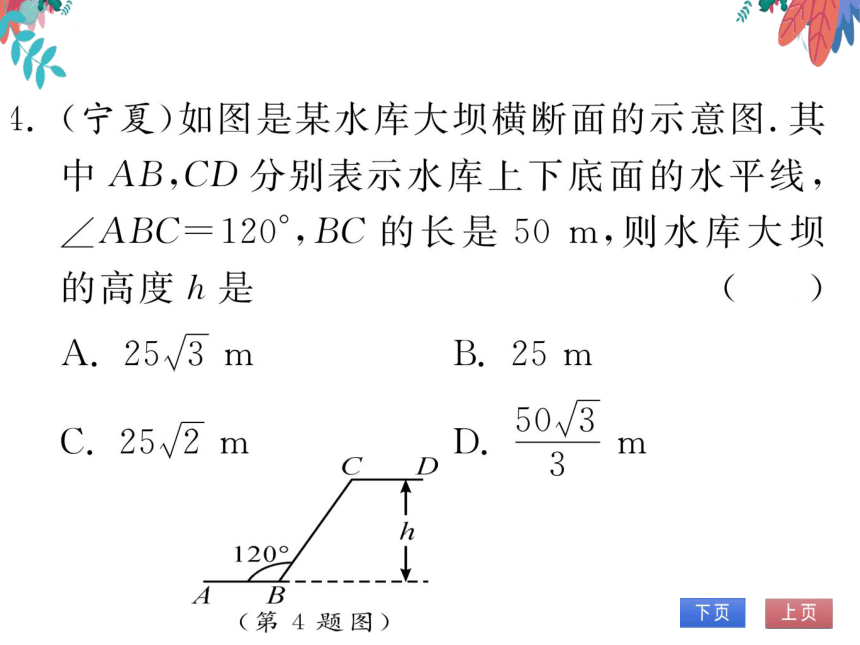
(宁夏)如图是某水库大坝横断面的示意图.其
中AB,CD分别表示水库上下底面的水平线,
∠ABC=120°,BC的长是50m,则水库大坝
的高度h是
(A
A.253m
B.25m
50√3
C.25
h
120
B
(第4题图
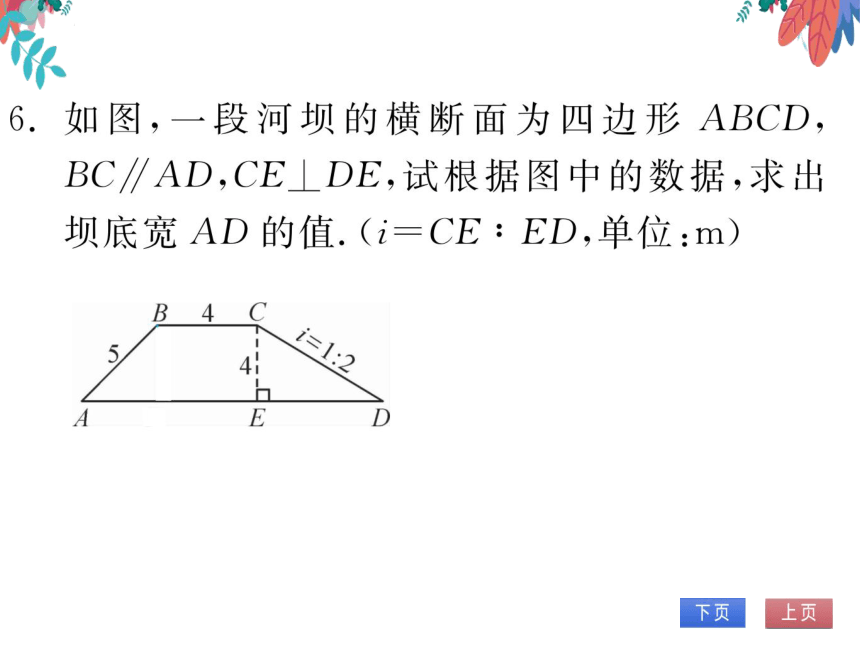
解:过点B作BF
B34
AD于点F,
可得矩形BCEF
F
E
EF=BC-4 BF=CE-4
在Rt△ABF中,
∠AFB=90°,AB=5,BF=4
由勾股定理可得AF=√AB2=BF2
4
又∵在Rt△CED中,
Ed 2
。ED=2CE=2×4=8
AD=AF+FE+ED=3+4+8=15(
知识点2坐标系中的直线与x轴的夹角
7.直线y=x的向上方向与x轴正方向所夹的锐
角为
A.30°
B.45°
C.60°
D,90°
8.直线y=2x+1的向上方向与x轴正方向所夹
的锐角为a,则tana=2
9.已知正比例函数y=kx经过点(2,3),则该直
线的向上方向与x轴正方向所夹的锐角的正
切值为
0.已知直线y=kx经过点(3,3),求直线的向
上方向与x轴正方向所夹的锐角a
解:将(3,3)代入y=kx,得
3k,即k
tan a
又∵a是锐角,
a=30
课后作业
全面提升
如图,某水渠的横断面
是四边形ABCD,其中
AB∥EF∥GH,已知
B
其斜坡AD和BC的坡度均为1:0.6,现测得
放水前的水面宽EF为1.2m,当水闸放水后,
水渠内水面宽GH为2.1m.求放水后水面上
升的高度是
A.0.55m
B.0.8m
课前预习
预习新知
小明爬一土坡,他从A处爬到B处所走的直线
距离AB=4m,此时,他离地面的高度h=2
则这个土坡的坡角∠A=30°;土坡AB的
坡度为1:3
2.P1(x1,y1),P2(x2,y2)是直线y=kx+b(k
0)上的任意两点,这条直线向上方向与x轴正
方向所夹的锐角为α,则tana
k
当堂训练
巩固基础
知识点1坡度、坡角问题
1.一斜坡的坡度为1:3,如果某人站的位置的
水平宽度为6m,则他所在的位置的铅直高度
为
a2 m
B.18
D
2.某水库大坝的横断面是四边形ABDE,AE∥
BD,坝内斜坡的坡度i1=1:3,坝外斜坡的
坡度i2=1:1,则两个坡角的和为
A.90
B.60
D.105
3.如图,防洪大堤的横断面是四边形ABDE
AE∥BD,坝高AC为6m,背水坡AB的坡度
为1:2,则斜坡AB的长为
A.13m
B.6√5m
C.56m
D.14m
6 m
B
(第3题图)
(宁夏)如图是某水库大坝横断面的示意图.其
中AB,CD分别表示水库上下底面的水平线,
∠ABC=120°,BC的长是50m,则水库大坝
的高度h是
(A
A.253m
B.25m
50√3
C.25
h
120
B
(第4题图
解:过点B作BF
B34
AD于点F,
可得矩形BCEF
F
E
EF=BC-4 BF=CE-4
在Rt△ABF中,
∠AFB=90°,AB=5,BF=4
由勾股定理可得AF=√AB2=BF2
4
又∵在Rt△CED中,
Ed 2
。ED=2CE=2×4=8
AD=AF+FE+ED=3+4+8=15(
知识点2坐标系中的直线与x轴的夹角
7.直线y=x的向上方向与x轴正方向所夹的锐
角为
A.30°
B.45°
C.60°
D,90°
8.直线y=2x+1的向上方向与x轴正方向所夹
的锐角为a,则tana=2
9.已知正比例函数y=kx经过点(2,3),则该直
线的向上方向与x轴正方向所夹的锐角的正
切值为
0.已知直线y=kx经过点(3,3),求直线的向
上方向与x轴正方向所夹的锐角a
解:将(3,3)代入y=kx,得
3k,即k
tan a
又∵a是锐角,
a=30
课后作业
全面提升
如图,某水渠的横断面
是四边形ABCD,其中
AB∥EF∥GH,已知
B
其斜坡AD和BC的坡度均为1:0.6,现测得
放水前的水面宽EF为1.2m,当水闸放水后,
水渠内水面宽GH为2.1m.求放水后水面上
升的高度是
A.0.55m
B.0.8m
