【沪科版】数学九年级上册 第21章 二次函数与反比例函数 整合与提高 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第21章 二次函数与反比例函数 整合与提高 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览






文档简介
(共23张PPT)
考点专训
考点1函数表达式的确定
例1已知二次函数的图象经过点(1,0),顶点坐
标是(-2
求这个二次函数的表达式
解:由题意可设二次函数的表达式为y=a(x+
2)2+。,把x=1,y=0代入,得0=a(1+2)2+
解得
所以所求二次函数的表达式为
(x+2)2+。,即y
x2-2x+
考点2函数图象的综合应用
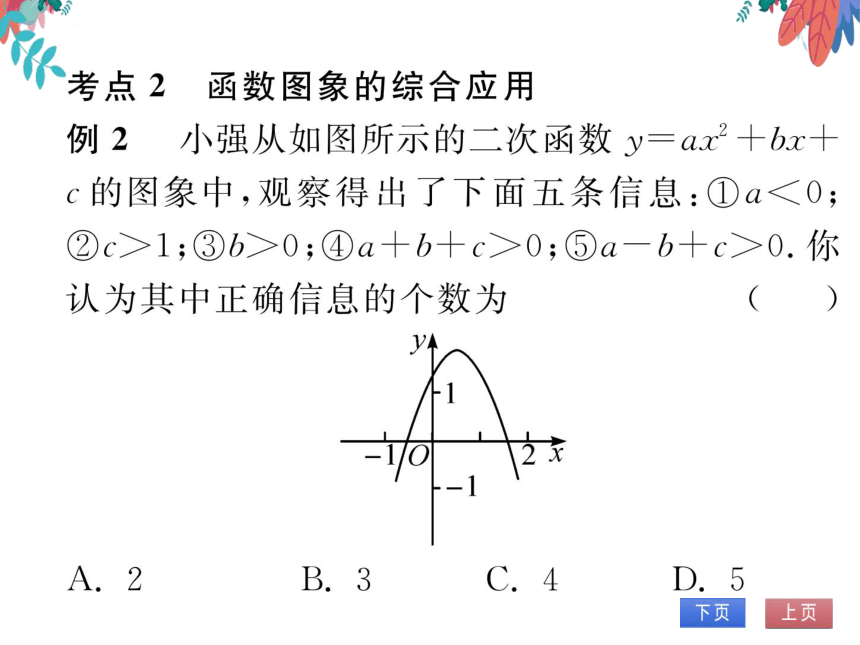
例2小强从如图所示的二次函数y=ax2+bx
c的图象中,观察得出了下面五条信息:①a<0
②c>1;③b>0;④a+b+c>0;⑤a-b+c>0.你
认为其中正确信息的个数为
解析】由抛物线开口向下,可知a<0,故①正确
x=0时,y=c,即抛物线y=ax2+bx+c与y
轴的交点坐标为(0,c),由图象可知c>1,故②正
b
确;由抛物线的对称轴在y轴右侧,可知
,即a,b异号,又a<0,所以b>0,故③正确;当
x=1时,y=a+b+c,由图象可知a+b+c>0,故
④正确;当x=-1时,y=a=b+c,由图象可知
a-b+c<0,故⑤不正确.综上可知,答案为(
考点3反比例函数
例3如图,直线y=x+m与双曲线y
x
相交
于A(2,1),B两点
(1)求m及k的值;
y=3+
(2)不解关于x,y的方程组
k
直接写出
点B的坐标;
解:(1)把A(2,1)分别代入直
k
线y=x+m与双曲线
中,得m=-1,k=2
23
(2)点B的坐标为(-1,-2)
(3)将x
72
1代入
2x+4m
2×(-1)+4×(-1)=2-4
所以直线y=-2x+4m经过点B(-1,-2)
归纳】此类题通常是给出交点的坐标,根据交点
坐标确定反比例函数和一定函数的表达式;或者
给出两个函数的图象,结合图象确定函数的表达
式;或者是确定两个函数图象的交点坐标.在解
题时,要注意反比例函数和一次函数的一般形
式,通过设一般形式,利用待定系数法确定函数
表达式.如果求两函数的交点坐标,那么要联立
两个函数的表达式,得到方程组,通过解方程组
求得交点的坐
考点4二次函数的实际应用
例4如图,在矩形ABCD中,AB=6cm,BC
Cm,点P从点A开始沿AB以1cm/s的速度
向点B移动,点Q从点B开始沿BC以2cm
的速度向点C移动,且P,Q中有一点到达终点就
停止移动.若点P,Q分别从点A,B同时出发,设
移动时间为ts(t>0),△DPQ的面积为Scm2,
求S关于t的函数关系式,并求出S的最小值
考点专训
考点1函数表达式的确定
例1已知二次函数的图象经过点(1,0),顶点坐
标是(-2
求这个二次函数的表达式
解:由题意可设二次函数的表达式为y=a(x+
2)2+。,把x=1,y=0代入,得0=a(1+2)2+
解得
所以所求二次函数的表达式为
(x+2)2+。,即y
x2-2x+
考点2函数图象的综合应用
例2小强从如图所示的二次函数y=ax2+bx
c的图象中,观察得出了下面五条信息:①a<0
②c>1;③b>0;④a+b+c>0;⑤a-b+c>0.你
认为其中正确信息的个数为
解析】由抛物线开口向下,可知a<0,故①正确
x=0时,y=c,即抛物线y=ax2+bx+c与y
轴的交点坐标为(0,c),由图象可知c>1,故②正
b
确;由抛物线的对称轴在y轴右侧,可知
,即a,b异号,又a<0,所以b>0,故③正确;当
x=1时,y=a+b+c,由图象可知a+b+c>0,故
④正确;当x=-1时,y=a=b+c,由图象可知
a-b+c<0,故⑤不正确.综上可知,答案为(
考点3反比例函数
例3如图,直线y=x+m与双曲线y
x
相交
于A(2,1),B两点
(1)求m及k的值;
y=3+
(2)不解关于x,y的方程组
k
直接写出
点B的坐标;
解:(1)把A(2,1)分别代入直
k
线y=x+m与双曲线
中,得m=-1,k=2
23
(2)点B的坐标为(-1,-2)
(3)将x
72
1代入
2x+4m
2×(-1)+4×(-1)=2-4
所以直线y=-2x+4m经过点B(-1,-2)
归纳】此类题通常是给出交点的坐标,根据交点
坐标确定反比例函数和一定函数的表达式;或者
给出两个函数的图象,结合图象确定函数的表达
式;或者是确定两个函数图象的交点坐标.在解
题时,要注意反比例函数和一次函数的一般形
式,通过设一般形式,利用待定系数法确定函数
表达式.如果求两函数的交点坐标,那么要联立
两个函数的表达式,得到方程组,通过解方程组
求得交点的坐
考点4二次函数的实际应用
例4如图,在矩形ABCD中,AB=6cm,BC
Cm,点P从点A开始沿AB以1cm/s的速度
向点B移动,点Q从点B开始沿BC以2cm
的速度向点C移动,且P,Q中有一点到达终点就
停止移动.若点P,Q分别从点A,B同时出发,设
移动时间为ts(t>0),△DPQ的面积为Scm2,
求S关于t的函数关系式,并求出S的最小值
