【沪科版】数学九年级上册 第21章 专题一 二次函数的图象与性质的综合应用 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第21章 专题一 二次函数的图象与性质的综合应用 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
类型1求抛物线的表达式
(天津)已知抛物线y=x2-4x+3与x轴相交
于点A,B(点A在点B左侧),顶点为M,平移
该抛物线,使点M平移后的对应点M落在x
轴上,点B平移后的对应点B落在y轴上,则
平移后的抛物线的表达式为
x2-2x+1
D
x2-2x-1
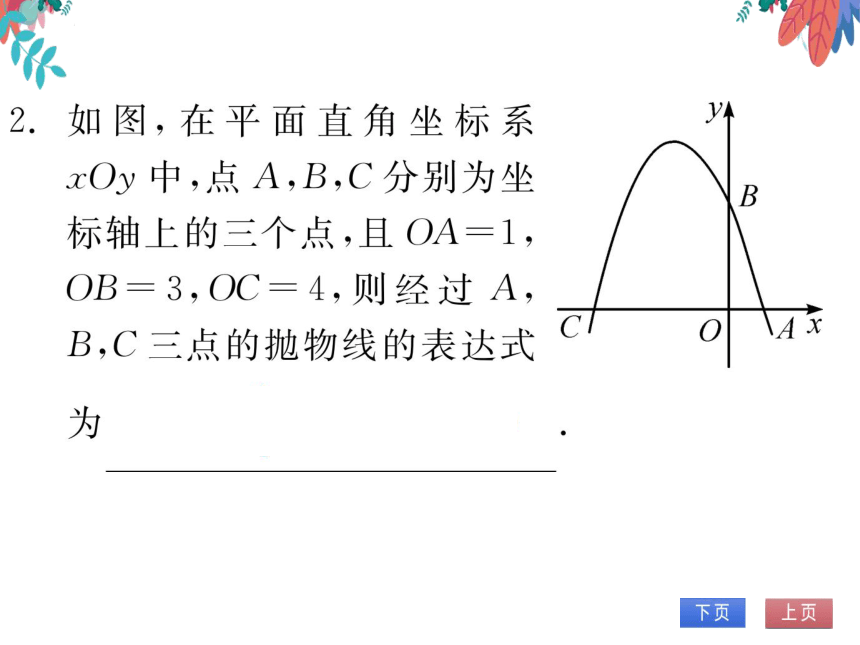
图,在平面直角坐标系
xO中,点A,B,C分别为坐
B
标轴上的三个点,且OA=1,
OB=3,OC=4,则经过A,
B,C三点的抛物线的表达式
O
AI
为
(x+4)(x-1)
已知顶点坐标为(-2,-1)的抛物线交x轴于
A,B两点(A点在B点的左边),且AB=2,求
抛物线对应的函数表达式
解:设函数表达式为y=a(x+2)2-1
对称轴为直线x=-2,AB
A(-3,0),B(-1,0).当x=-1时
0
代入表达式,得
(x+2)2-1
x2+4x+
4
解:∵对称轴x
2,A(1,0),∴B(3
△ABC
AB·OC=2,即。×2
OC=2.∴OC=2,C(0,2)或(0,-2).∴b
士2.当b=2时,A(1,0),a≈2
x2-x+2.同理,当b=-2时,a
+-x-2.
类型2二次函数与一元二次方程或不等式
5.(南京)已知函数y=-x2+(m-1)x+m(m
为常数),该函数的图象与x轴公共点的个数
是
D)
B.
D.1或
鄂州)如图,抛物线y=ax2+bx+c的图象交
x轴于点A(-2,0)和点B,交y轴负半轴于
点C,且OB=OC,下列结论:①2b-c=2;
③aC=b
0.其中正确结
论的个数是
X
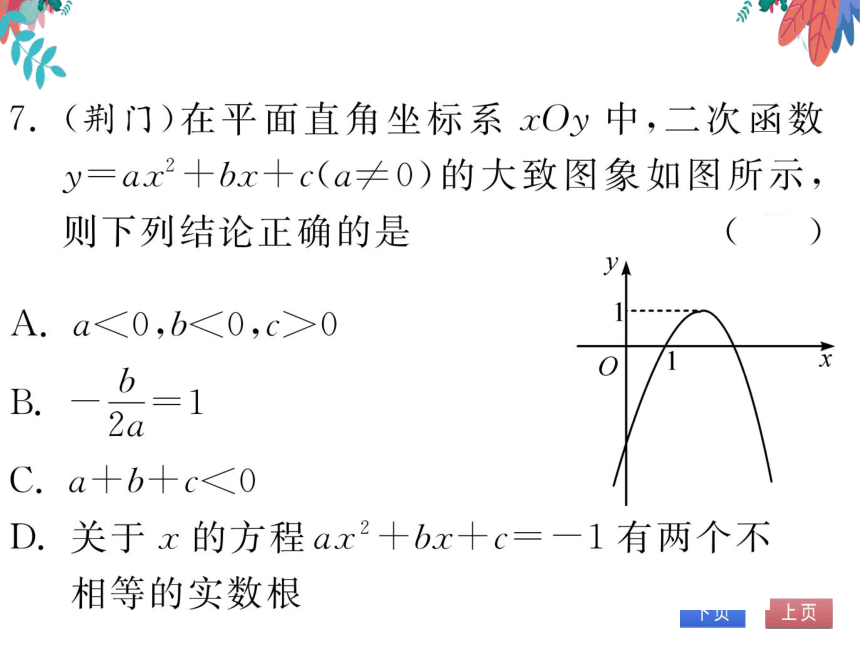
(荆门)在平面直角坐标系xOy中,次函数
y=ax2+bx+c(a≠0)的大致图象如图所示
则下列结论正确的是
A.a<0,b<0,c>0
b
0
D.关于x的方程ax2+bx+c=-1有两个不
相等的实数根
8.(咸宁)如图,直线y=mx+n与抛物线y=ax
bx+c交于A(-1,p),B(4,q)两点,则关于x
的不等式mx+n>ax2+bx+c的解集
是x<-1或x>4
9.如图,抛物线y1=-x2+2x+3与直线y2=4x
交于A,B两点,抛物线交x轴于C,D两点
(1)求A,B,C,D四点的坐标;
(2)根据图象,直接写出不等式-x2+2x+3<
0和-x2+2x+3>4x的解集
解:(1)A(1,4),B(-3,-12),
C(-1,0),D(3,0)
(2)不等式-x2+2x+3<0的
C/NO D
解集是x<-1或x>3,不等
式-x2+2x+3>4x的解集是
3B
类型1求抛物线的表达式
(天津)已知抛物线y=x2-4x+3与x轴相交
于点A,B(点A在点B左侧),顶点为M,平移
该抛物线,使点M平移后的对应点M落在x
轴上,点B平移后的对应点B落在y轴上,则
平移后的抛物线的表达式为
x2-2x+1
D
x2-2x-1
图,在平面直角坐标系
xO中,点A,B,C分别为坐
B
标轴上的三个点,且OA=1,
OB=3,OC=4,则经过A,
B,C三点的抛物线的表达式
O
AI
为
(x+4)(x-1)
已知顶点坐标为(-2,-1)的抛物线交x轴于
A,B两点(A点在B点的左边),且AB=2,求
抛物线对应的函数表达式
解:设函数表达式为y=a(x+2)2-1
对称轴为直线x=-2,AB
A(-3,0),B(-1,0).当x=-1时
0
代入表达式,得
(x+2)2-1
x2+4x+
4
解:∵对称轴x
2,A(1,0),∴B(3
△ABC
AB·OC=2,即。×2
OC=2.∴OC=2,C(0,2)或(0,-2).∴b
士2.当b=2时,A(1,0),a≈2
x2-x+2.同理,当b=-2时,a
+-x-2.
类型2二次函数与一元二次方程或不等式
5.(南京)已知函数y=-x2+(m-1)x+m(m
为常数),该函数的图象与x轴公共点的个数
是
D)
B.
D.1或
鄂州)如图,抛物线y=ax2+bx+c的图象交
x轴于点A(-2,0)和点B,交y轴负半轴于
点C,且OB=OC,下列结论:①2b-c=2;
③aC=b
0.其中正确结
论的个数是
X
(荆门)在平面直角坐标系xOy中,次函数
y=ax2+bx+c(a≠0)的大致图象如图所示
则下列结论正确的是
A.a<0,b<0,c>0
b
0
D.关于x的方程ax2+bx+c=-1有两个不
相等的实数根
8.(咸宁)如图,直线y=mx+n与抛物线y=ax
bx+c交于A(-1,p),B(4,q)两点,则关于x
的不等式mx+n>ax2+bx+c的解集
是x<-1或x>4
9.如图,抛物线y1=-x2+2x+3与直线y2=4x
交于A,B两点,抛物线交x轴于C,D两点
(1)求A,B,C,D四点的坐标;
(2)根据图象,直接写出不等式-x2+2x+3<
0和-x2+2x+3>4x的解集
解:(1)A(1,4),B(-3,-12),
C(-1,0),D(3,0)
(2)不等式-x2+2x+3<0的
C/NO D
解集是x<-1或x>3,不等
式-x2+2x+3>4x的解集是
3
