【沪科版】数学九年级上册 第22章 相似形 整合与提高 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第22章 相似形 整合与提高 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览





文档简介
(共26张PPT)
考点专训
考点1相似三角形的判定
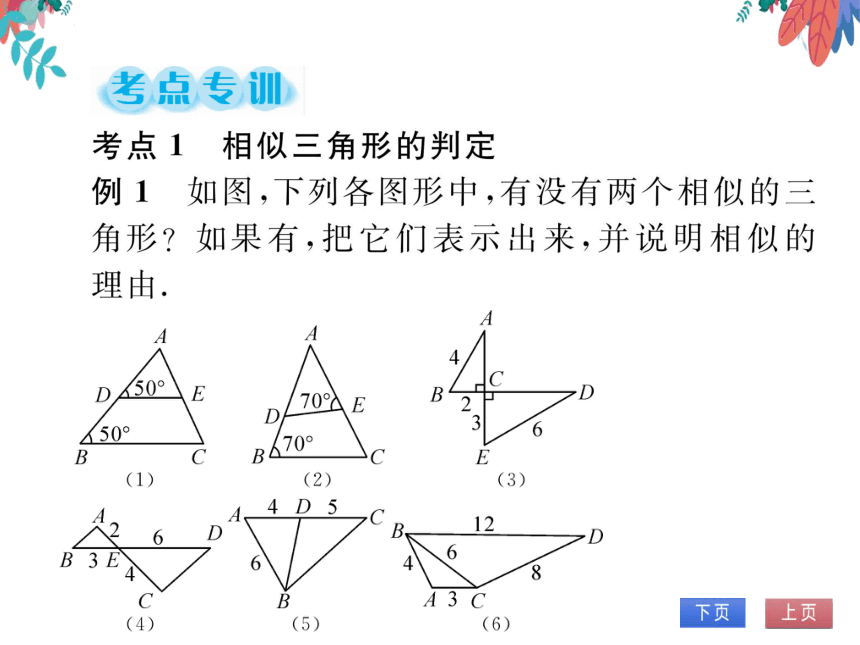
例1如图,下列各图形中,有没有两个相似的三
角形 如果有,把它们表示出来,并说明相似的
理由
50°
C
E
70°E
B
D
50
70°
B
B
E
(1)
(2)
(3)
4D5
C
2
6
B
b E
6
8
B
A3 C
(4
分析】相似三角形的判定可类比全等三角形的
判定,一般都是先找对应角,在这个过程中,要特
别注意公共角、对顶角、同角的余角(或补角)、等
角的余角(或补角)等都是相等的.本题(5)中包
含三个三角形,因此要逐个研究三个三角形的每
两个三角形的关系,不要遗漏
解:(1)△ADE∽△ABC.理由:∵∠ADE
ABC=50
A=∠A,∴△ADE∽△ABC
(2)△AED△ABC.理由:∴∠A=∠A
AED=∠ABC=70,∴△AED∽△ABC
(3)△ABC∽△DEC.理由:在Rt△ABC和Rt△DEC中,
bc2 AB 4 2 AC
42-2
122
Ec
DE 6
27
BC AB AC
EC DE CD
ABC△DEC
4)△ABE∽△CDE.理由:∵∠AEB=∠CED,
Ae 1 BE 3
AE BE
CE 2 E6 2
即
E DE
△ABE∽△CDE
CA 9
(5)△CAB∽△BAD.理由:∵∠A=∠A
ba 6
AB 6
CA AB
AD BA AD
CAB∽△BAD
(6)△ABC△CDB.理由:…A
CB 6
AB 41 BC 6
ACAB BC
cd8 2B 12 2 CB CD DB
ABC△CDB
元素,故用定义判定两个三角形相似在实际操作
中并不常用
(2)利用“定理2”进行判定时,一定注意是“夹
角”,并非任意角
3)当给出的两个三角形中的已知条件以角度为
主时,我们应首先使用“两角对应相等”的判
定方法;当给出的已知条件为边、角混杂时
我们应首先考虑使用“两边对应成比例且夹
角相等”的判定方法;当给出的已知条件都是
边长时,我们应首先考虑使用“三边对应成比
例”的判定方法
考点2相似三角形的判定与函数的综合
例2如图,正方形ABCD的边长为1,点E是
AD边上的动点,从点A沿AD向点D运动,以
BE为边,在BE的上方作正方形BEFG,连接
CG.请探究:
(1)线段AE与CG是否相等 请说明理由;
(2)若设AE=x,DH=y,当x取何值时,y最大
(3连接BH,当点E运动到AD的何位置时
BEH∽△BAE
考点专训
考点1相似三角形的判定
例1如图,下列各图形中,有没有两个相似的三
角形 如果有,把它们表示出来,并说明相似的
理由
50°
C
E
70°E
B
D
50
70°
B
B
E
(1)
(2)
(3)
4D5
C
2
6
B
b E
6
8
B
A3 C
(4
分析】相似三角形的判定可类比全等三角形的
判定,一般都是先找对应角,在这个过程中,要特
别注意公共角、对顶角、同角的余角(或补角)、等
角的余角(或补角)等都是相等的.本题(5)中包
含三个三角形,因此要逐个研究三个三角形的每
两个三角形的关系,不要遗漏
解:(1)△ADE∽△ABC.理由:∵∠ADE
ABC=50
A=∠A,∴△ADE∽△ABC
(2)△AED△ABC.理由:∴∠A=∠A
AED=∠ABC=70,∴△AED∽△ABC
(3)△ABC∽△DEC.理由:在Rt△ABC和Rt△DEC中,
bc2 AB 4 2 AC
42-2
122
Ec
DE 6
27
BC AB AC
EC DE CD
ABC△DEC
4)△ABE∽△CDE.理由:∵∠AEB=∠CED,
Ae 1 BE 3
AE BE
CE 2 E6 2
即
E DE
△ABE∽△CDE
CA 9
(5)△CAB∽△BAD.理由:∵∠A=∠A
ba 6
AB 6
CA AB
AD BA AD
CAB∽△BAD
(6)△ABC△CDB.理由:…A
CB 6
AB 41 BC 6
ACAB BC
cd8 2B 12 2 CB CD DB
ABC△CDB
元素,故用定义判定两个三角形相似在实际操作
中并不常用
(2)利用“定理2”进行判定时,一定注意是“夹
角”,并非任意角
3)当给出的两个三角形中的已知条件以角度为
主时,我们应首先使用“两角对应相等”的判
定方法;当给出的已知条件为边、角混杂时
我们应首先考虑使用“两边对应成比例且夹
角相等”的判定方法;当给出的已知条件都是
边长时,我们应首先考虑使用“三边对应成比
例”的判定方法
考点2相似三角形的判定与函数的综合
例2如图,正方形ABCD的边长为1,点E是
AD边上的动点,从点A沿AD向点D运动,以
BE为边,在BE的上方作正方形BEFG,连接
CG.请探究:
(1)线段AE与CG是否相等 请说明理由;
(2)若设AE=x,DH=y,当x取何值时,y最大
(3连接BH,当点E运动到AD的何位置时
BEH∽△BAE
