【沪科版】数学九年级上册 第22章 专题四 相似三角形的综合运用 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第22章 专题四 相似三角形的综合运用 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览


文档简介
(共23张PPT)
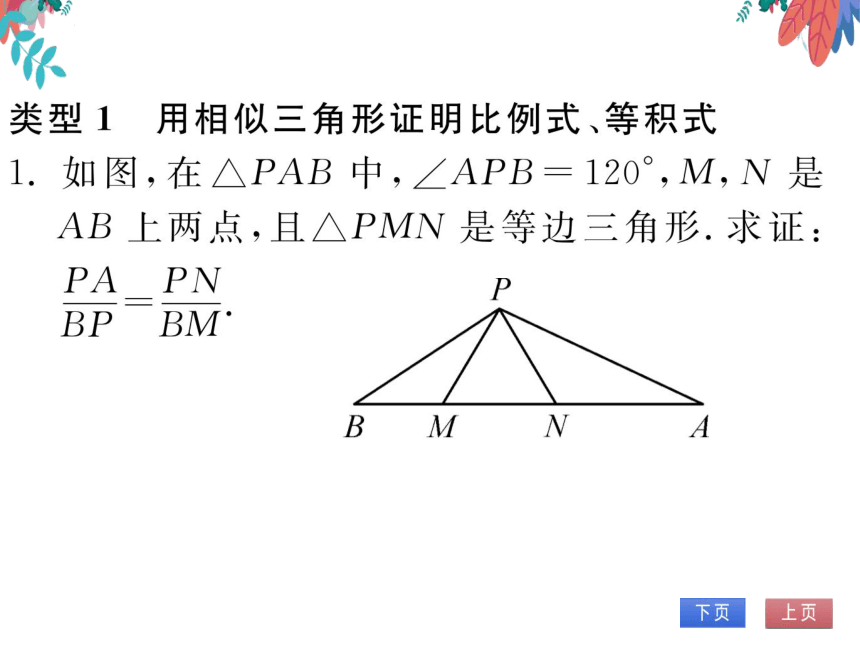
类型1用相似三角形证明比例式、等积式
如图,在△PAB中,∠APB=120°,M,N是
AB上两点,且△PMN是等边三角形.求证:
PA PN
BP BM
证明:∵△PMN为等边
角形,
PMN
PNM
B M
MPN=60
∠BMP=∠PNA=120°
BPA=120
∠BPM+∠APN=60
在△BMP中,∠B+∠BPM=60
∠B=∠NPA
PA PN
△BMP∽△PNA
BP BM
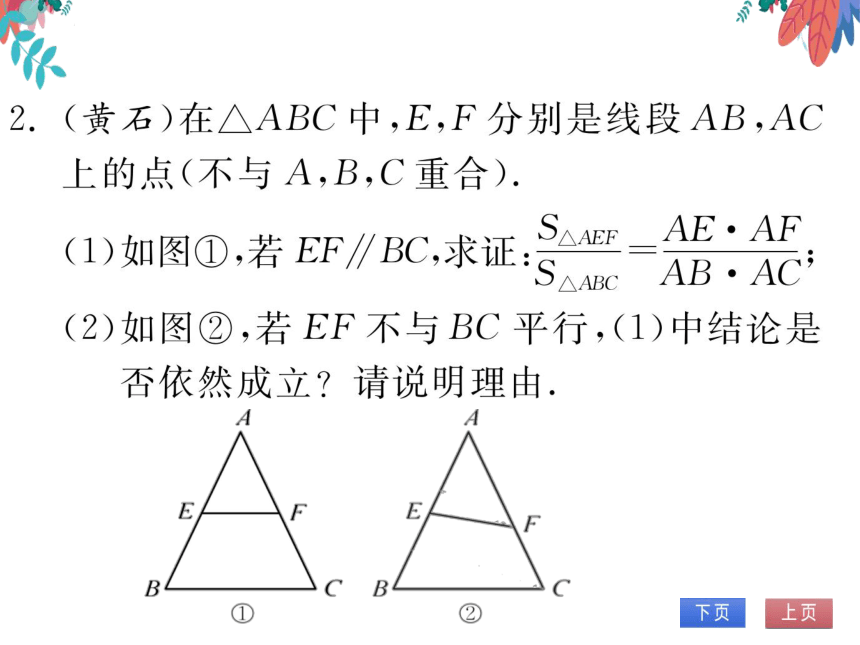
2.(黄石)在△ABC中,E,F分别是线段AB,AC
上的点(不与A,B,C重合)
(1)如图①,若EF∥BC,求证
△AEF
AE·AF
△ABC
AB·AC
(2)如图②,若EF不与BC平行,(1)中结论是
否依然成立 请说明理由
/
E
B
C B
E
F
B
c B
1)证明:∵EF∥BC,∴△AEF∽△ABC
AE AF
AB AC
△AEF
AE
A AF AEAF
S
△AB
AB
AB AC AB . AC
(2)解:若EF不与BC平行,(1)中结论仍然成
立,分别过F,C作AB的垂线,垂足分别为
NH
FN⊥AB,CH⊥AB,
FN∥CH
AFN△ACH
FN AF
CH AC
△AEF
121
AE FN
AE.AF
△ABC
AB·CAB.AC
类型2用相似三角形证明线段相等
如图,在矩形ABCD的CD边上任取一点E
使AE2=AB·AD,作BF⊥AE于点F.求证
BF=AE
证明:∵∠DAE+∠BAE=90
F
ABF+∠BAF=90°
E
∠DAE=∠ABF.
Rt△ ALERT△BFA
B
AE AD
BABF·
AE AD
又∵AE=AB· AD,AB AF.②
ADAD
由①②,得
BFAE,、BF=AE
尸/R
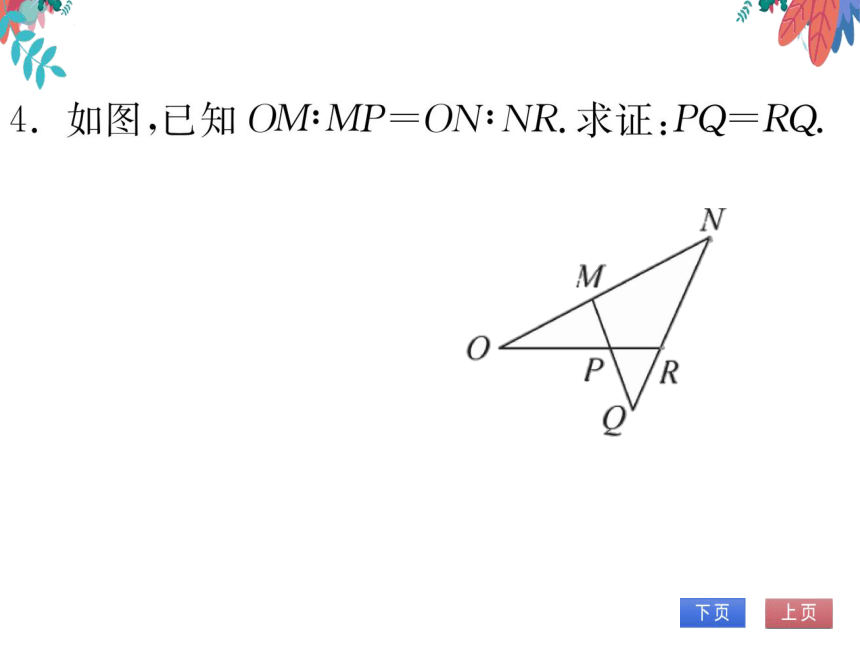
证明:过点N作NK∥MQ
交OR的延长线于点K
△OMP△ONK
O
P/
△PQR∽△KNR
OM MP
ON NK
PQ RQ
KN RN
OM MP
又OM:MP=ON:NR
ON NR
MP MP
由①③,得
NK NR
NR=NK.④
由②④,得PQ=RQ
类型3用相似三角形解决有关计算问题
5.(江西)如图,在△ABC中,AB=8,BC=4,
AC=6,CD∥AB,BD是∠ABC的平分线
BD交AC于E点,求AE的长
解:·BD是∠ABC的平分
线,∴∠ABD=∠CBD
CD∥AB,
E
∠ABD=∠D
∠CBD=∠D.
B
CD=BC-4
类型1用相似三角形证明比例式、等积式
如图,在△PAB中,∠APB=120°,M,N是
AB上两点,且△PMN是等边三角形.求证:
PA PN
BP BM
证明:∵△PMN为等边
角形,
PMN
PNM
B M
MPN=60
∠BMP=∠PNA=120°
BPA=120
∠BPM+∠APN=60
在△BMP中,∠B+∠BPM=60
∠B=∠NPA
PA PN
△BMP∽△PNA
BP BM
2.(黄石)在△ABC中,E,F分别是线段AB,AC
上的点(不与A,B,C重合)
(1)如图①,若EF∥BC,求证
△AEF
AE·AF
△ABC
AB·AC
(2)如图②,若EF不与BC平行,(1)中结论是
否依然成立 请说明理由
/
E
B
C B
E
F
B
c B
1)证明:∵EF∥BC,∴△AEF∽△ABC
AE AF
AB AC
△AEF
AE
A AF AEAF
S
△AB
AB
AB AC AB . AC
(2)解:若EF不与BC平行,(1)中结论仍然成
立,分别过F,C作AB的垂线,垂足分别为
NH
FN⊥AB,CH⊥AB,
FN∥CH
AFN△ACH
FN AF
CH AC
△AEF
121
AE FN
AE.AF
△ABC
AB·CAB.AC
类型2用相似三角形证明线段相等
如图,在矩形ABCD的CD边上任取一点E
使AE2=AB·AD,作BF⊥AE于点F.求证
BF=AE
证明:∵∠DAE+∠BAE=90
F
ABF+∠BAF=90°
E
∠DAE=∠ABF.
Rt△ ALERT△BFA
B
AE AD
BABF·
AE AD
又∵AE=AB· AD,AB AF.②
ADAD
由①②,得
BFAE,、BF=AE
尸/R
证明:过点N作NK∥MQ
交OR的延长线于点K
△OMP△ONK
O
P/
△PQR∽△KNR
OM MP
ON NK
PQ RQ
KN RN
OM MP
又OM:MP=ON:NR
ON NR
MP MP
由①③,得
NK NR
NR=NK.④
由②④,得PQ=RQ
类型3用相似三角形解决有关计算问题
5.(江西)如图,在△ABC中,AB=8,BC=4,
AC=6,CD∥AB,BD是∠ABC的平分线
BD交AC于E点,求AE的长
解:·BD是∠ABC的平分
线,∴∠ABD=∠CBD
CD∥AB,
E
∠ABD=∠D
∠CBD=∠D.
B
CD=BC-4
