【沪科版】数学九年级上册 第23章 解直角三角形 整合与提高 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第23章 解直角三角形 整合与提高 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览





文档简介
(共22张PPT)
考点专训
考点1锐角三角函数
例1(烟台)在Rt△ABC中,∠C=90°,AB=2
BC=√3,则
Sin
的值为
【解析】由正弦的定义,得snA_BC√3
AB
故∠A=60°
Sin
sin 3o
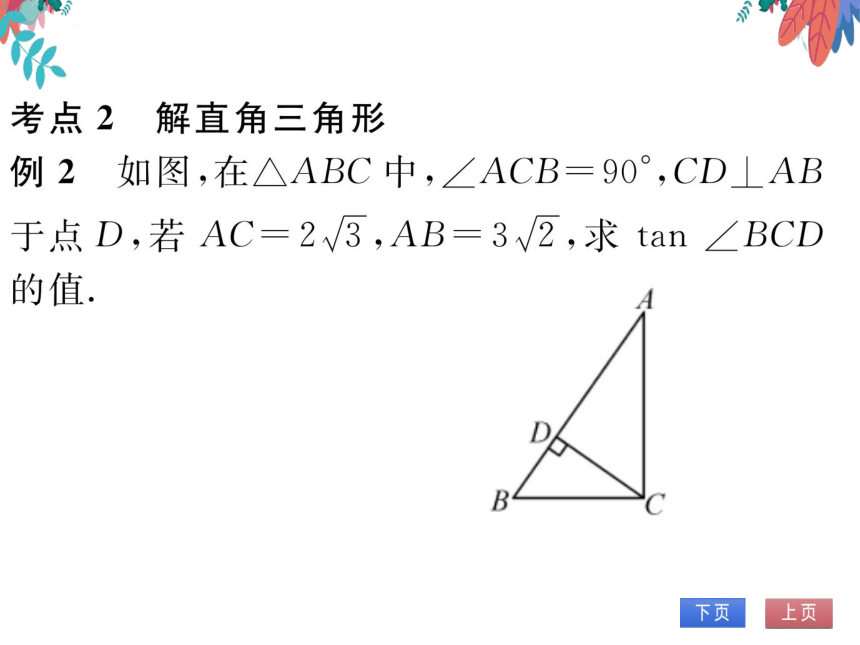
考点2解直角三角形
例2如图,在△ABC中,∠ACB=90°,CD⊥AB
于点D,若AC=2√3,AB=3√2,求tan∠BCD
值
解析】本题有两种解法:一种是在Rt△BCD
中求tan∠BCD,这需要我们利用△BCDc
△BAC求出△BCD的两直角边长;一种是利
用∠BCD=∠A的关系,在R△ABC中求
tanA(即tan∠BCD
B
解法一:在Rt△ABC中,根据勾股定理,得
BO
AB-AC
DBO
ABC,∠BDC
ACB=90
BC BD CD
BD CD
△BCD△BAC
AB BC AC
BD 2
解得BD=2,CD=2.∴tan∠BCD
解法二:在Rt△ABC中,根据勾股定理,得BC
AB-AC
6,"∠BCD+∠ACD=∠A+∠ACD=90°
BO
∠BCD=∠A.∴.tan∠BCD=tanA
Ac
例3如图,在Rt△ABC中,∠C=90°,点D是
BC的中点,DE⊥AB于点E,tanB=a,AE=7,
求DE的长
DE AC 1
解:∵tanB
BE BC 2
设
DE=x(x>0),则BE=2x
在Rt△BDE中,BD=√BE+DE
B
(2.x
又点D是BC的中点,BC=25x,AC=0×25x=5x
X AE=7,.AB=+=2x+7
在Rt△ABC中,AC+BC=AB2,
x2=一1(不合题意,舍去),即DE的长冬
(5x)2+(25x)2=(2x+7)2,化简,得3x2-4x-7
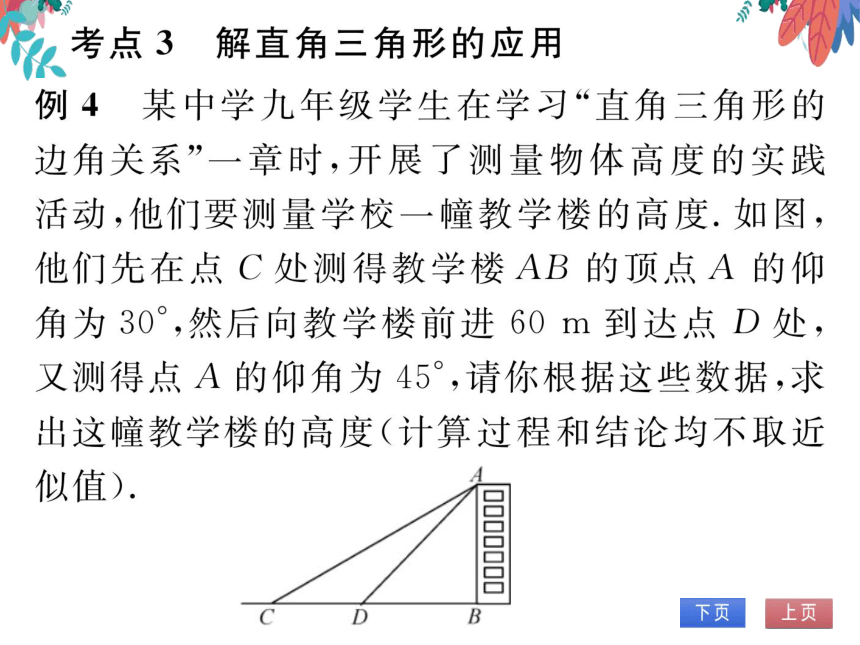
考点3解直角三角形的应用
例4某中学九年级学生在学习“直角三角形的
边角关系”一章时,开展了测量物体高度的实践
活动,他们要测量学校一幢教学楼的高度.如图
他们先在点C处测得教学楼AB的顶点A的仰
角为30°,然后向教学楼前进60m到达点D处
又测得点A的仰角为45°,请你根据这些数据,求
出这幢教学楼的高度(计算过程和结论均不取近
似值)
解:由已知可得∠ACB=30°
ADB=45°,CD=60m.设
AB=xm,在Rt△ABD中,
Bd=AB-x m
在Rt△ABC中,:tanC
B
AB
BC
BO
tan
tan 30
x(m).∵BC-BD=CD,∴3x-x=60,即(3-1)x
60
60.。。x
30(3+1)
教学楼的高度为30(3+1)m
考点专训
考点1锐角三角函数
例1(烟台)在Rt△ABC中,∠C=90°,AB=2
BC=√3,则
Sin
的值为
【解析】由正弦的定义,得snA_BC√3
AB
故∠A=60°
Sin
sin 3o
考点2解直角三角形
例2如图,在△ABC中,∠ACB=90°,CD⊥AB
于点D,若AC=2√3,AB=3√2,求tan∠BCD
值
解析】本题有两种解法:一种是在Rt△BCD
中求tan∠BCD,这需要我们利用△BCDc
△BAC求出△BCD的两直角边长;一种是利
用∠BCD=∠A的关系,在R△ABC中求
tanA(即tan∠BCD
B
解法一:在Rt△ABC中,根据勾股定理,得
BO
AB-AC
DBO
ABC,∠BDC
ACB=90
BC BD CD
BD CD
△BCD△BAC
AB BC AC
BD 2
解得BD=2,CD=2.∴tan∠BCD
解法二:在Rt△ABC中,根据勾股定理,得BC
AB-AC
6,"∠BCD+∠ACD=∠A+∠ACD=90°
BO
∠BCD=∠A.∴.tan∠BCD=tanA
Ac
例3如图,在Rt△ABC中,∠C=90°,点D是
BC的中点,DE⊥AB于点E,tanB=a,AE=7,
求DE的长
DE AC 1
解:∵tanB
BE BC 2
设
DE=x(x>0),则BE=2x
在Rt△BDE中,BD=√BE+DE
B
(2.x
又点D是BC的中点,BC=25x,AC=0×25x=5x
X AE=7,.AB=+=2x+7
在Rt△ABC中,AC+BC=AB2,
x2=一1(不合题意,舍去),即DE的长冬
(5x)2+(25x)2=(2x+7)2,化简,得3x2-4x-7
考点3解直角三角形的应用
例4某中学九年级学生在学习“直角三角形的
边角关系”一章时,开展了测量物体高度的实践
活动,他们要测量学校一幢教学楼的高度.如图
他们先在点C处测得教学楼AB的顶点A的仰
角为30°,然后向教学楼前进60m到达点D处
又测得点A的仰角为45°,请你根据这些数据,求
出这幢教学楼的高度(计算过程和结论均不取近
似值)
解:由已知可得∠ACB=30°
ADB=45°,CD=60m.设
AB=xm,在Rt△ABD中,
Bd=AB-x m
在Rt△ABC中,:tanC
B
AB
BC
BO
tan
tan 30
x(m).∵BC-BD=CD,∴3x-x=60,即(3-1)x
60
60.。。x
30(3+1)
教学楼的高度为30(3+1)m
