【沪科版】数学九年级上册 第23章 专题八 解直角三角形的综合运用 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第23章 专题八 解直角三角形的综合运用 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览





文档简介
(共17张PPT)
类型1解直角三角形与相似三角形结合
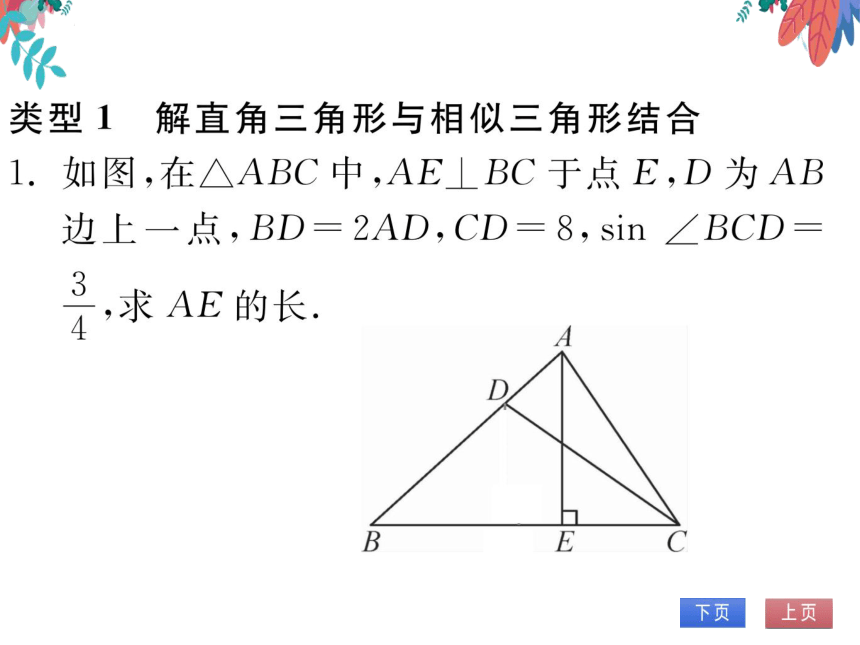
如图,在△ABC中,AE⊥BC于点E,D为AB
边上一点,BD=2AD,CD=8,sin∠BCD
求AE的长
B
E
解:过点D作DM⊥BC
于点M.
在Rt△DCM中,CD
8,sin∠BCD
4
B
M E
DM=CD·sin/BCD=8
AE
AE∥DM,
ABE
△DBM.·D
Ab 3
AE==9
2.(衢州)如图,已知“人字梯”(AB=AC)的
踩档把梯子等分成6份,从上往下的第二个踩
档与第三个踩档的正中间处有一条60cm长
的绑绳EF,tana
求“人字梯”的顶端离地
面的高AD.
解:设AD与EF交于点O
AFO△ACD,OF=EF
OF AF
30(cm),
DC AC
30
B
D
CD=72 cm
D
tan a
2 c 2
AD 5
72=180(cm)
答:“人字梯”的顶端离地面的高AD为
类型2解直角三角形与反比例函数结合
3.(荆州)如图,在平面直角坐标系中,O为原点
直线AB分别与x轴、y轴交于B,A两点,与
反比例函数的图象交于C,D两点,CE⊥x轴
于点E,tan∠ABO=,OB=4,OE=2
(1)求直线AB和反比例函数的表达式
2)求△OCD的面积
OA
解:(1)∵tan∠ABO
OB
CE 1 OA CE 1
B
be 2
EO
OA=2,CE=3,
A(0,2),C(-2,3)
由待定系数法易得直线AB的函数表达式为
y=-x+2,反比例函数的表达式为y
(2)将y
2x+2与y
联立,解得
。D(6,—1)
△OCD
△BOC
+
△BOD
4×3+×4
4.如图,在x轴的上方,直角∠BOA绕原点O按
顺时针方向旋转,若∠BOA的两边分别与函
数
的图象交于B,A两点,问
OAB的大小是否变化,请说明理由
解:分别过点A,B
作AN⊥x轴于点
N,BM⊥x轴于点
B
M.∴∠AOB=90
BOM+∠AON
M O N
∠AON+∠OAN=90°.∴.∠BOM=∠OAN
∠BMO=∠ANO=90
BOM△OAN
BM OM
A(n,-),则BM
72
72
72
AN 2
BM OM
OM
,.ON=n.由
●m7272
OB
AOB= 90
tanOAK
①
OB BM
△BOMo△OAN
DA ON
272
②,由①②知tan∠OAB=为定值
OAB的大小不变
类型1解直角三角形与相似三角形结合
如图,在△ABC中,AE⊥BC于点E,D为AB
边上一点,BD=2AD,CD=8,sin∠BCD
求AE的长
B
E
解:过点D作DM⊥BC
于点M.
在Rt△DCM中,CD
8,sin∠BCD
4
B
M E
DM=CD·sin/BCD=8
AE
AE∥DM,
ABE
△DBM.·D
Ab 3
AE==9
2.(衢州)如图,已知“人字梯”(AB=AC)的
踩档把梯子等分成6份,从上往下的第二个踩
档与第三个踩档的正中间处有一条60cm长
的绑绳EF,tana
求“人字梯”的顶端离地
面的高AD.
解:设AD与EF交于点O
AFO△ACD,OF=EF
OF AF
30(cm),
DC AC
30
B
D
CD=72 cm
D
tan a
2 c 2
AD 5
72=180(cm)
答:“人字梯”的顶端离地面的高AD为
类型2解直角三角形与反比例函数结合
3.(荆州)如图,在平面直角坐标系中,O为原点
直线AB分别与x轴、y轴交于B,A两点,与
反比例函数的图象交于C,D两点,CE⊥x轴
于点E,tan∠ABO=,OB=4,OE=2
(1)求直线AB和反比例函数的表达式
2)求△OCD的面积
OA
解:(1)∵tan∠ABO
OB
CE 1 OA CE 1
B
be 2
EO
OA=2,CE=3,
A(0,2),C(-2,3)
由待定系数法易得直线AB的函数表达式为
y=-x+2,反比例函数的表达式为y
(2)将y
2x+2与y
联立,解得
。D(6,—1)
△OCD
△BOC
+
△BOD
4×3+×4
4.如图,在x轴的上方,直角∠BOA绕原点O按
顺时针方向旋转,若∠BOA的两边分别与函
数
的图象交于B,A两点,问
OAB的大小是否变化,请说明理由
解:分别过点A,B
作AN⊥x轴于点
N,BM⊥x轴于点
B
M.∴∠AOB=90
BOM+∠AON
M O N
∠AON+∠OAN=90°.∴.∠BOM=∠OAN
∠BMO=∠ANO=90
BOM△OAN
BM OM
A(n,-),则BM
72
72
72
AN 2
BM OM
OM
,.ON=n.由
●m7272
OB
AOB= 90
tanOAK
①
OB BM
△BOMo△OAN
DA ON
272
②,由①②知tan∠OAB=为定值
OAB的大小不变
