【沪科版】数学九年级上册 23.1.2 第1课时 30度、45度、65度角的三角函数值 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 23.1.2 第1课时 30度、45度、65度角的三角函数值 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览





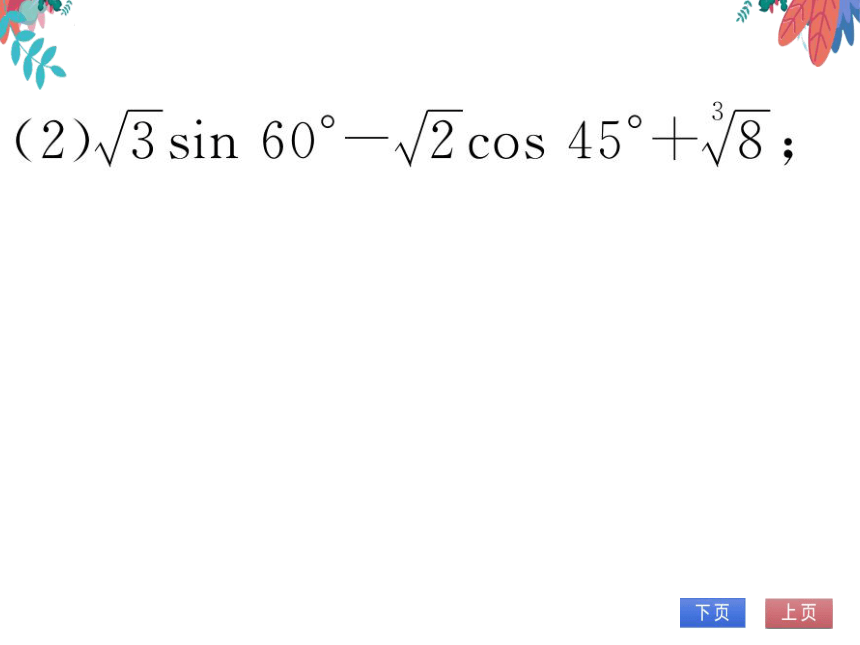
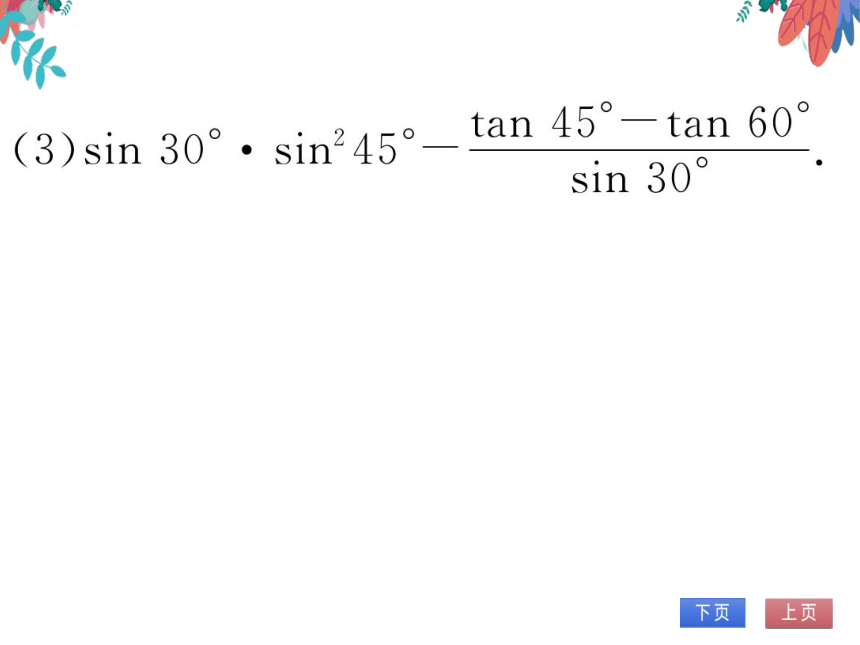

文档简介
(共24张PPT)
课前预习
领习新知
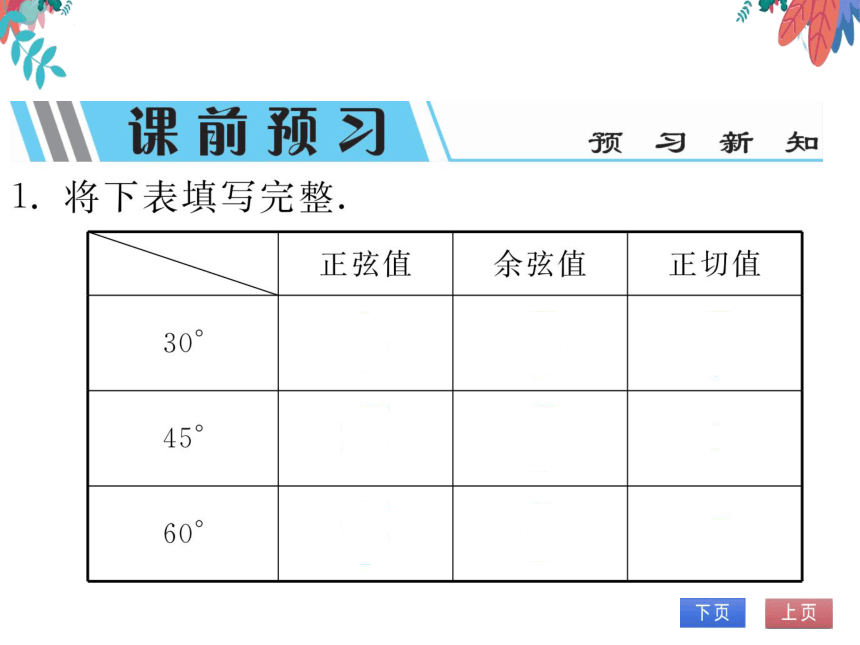
1.将下表填写完整
正弦值余弦值
正切值
30
45
60
当堂训练
巩固基础
知识点130°,45°,60角的三角函数值
(大庆)2cos60°的值为
B.√3
D
2.(无锡)sin45°的值为
B
B.
D
(天津)cOs30°的值为
A
D.√3
4.下列结论中正确的是
A.sin30°+sin40°=sin70
B.cos30+cos30°=cos60°
C.tan30°·tan60°=1
D. tan 30=tan 60
计算:
(1)2cos30°-tan45
(1-tan60°)2
解:原式=2
(2)3sin60°-√2cos45
解:原式
tan45—tan60
(3)sin30°·sin245°
sin30°
解:原式
知识点2根据特殊的三角函数值确定锐角的
度数
6.在Rt△ABC中,∠C=90°,若sinA
∠A的度数是
( A
C.60
若α为锐角,且tan(90°-a)=√3,则a为
A.30
B.45
C.60°
D,75°
8.在△ABC中,∠A,∠B都是锐角,且sinA
, COs
则△ABC的形状是(B
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
9.(本溪)在△ABC中,∠B=45°,cosA
∠C的度数是105
0.若3ana-2cos30°=0,则锐角a=30
1.若α为锐角,且sinα的值是方程2x2+3x
2=0的一个根,求a的度数及tana的值
解:由2x2+3x-2=0,得x1=-2
a为锐角,∴sina
a=30°..tana=tan30°
课后作业
全面提升
1.化简√(tan30°1)2等于
A
A.1
B.√3-1
D.√3+1
2.点M(-sin60°,-cos60°)关于x轴对称的点
的坐标是
B
D
212
3.在△ABC中,若sinA
tan b
0,则∠C的度数为
A.30°B.60°
C.90°
D,120°
4.已知a,B均为锐角,且满足sina
(tanB-1)2=0,则a+
计算:
(1)2cos230°-2sin60°·cos45
解:原式=2×
2×。Xy
(2)2sin60°-3tan30°
2019
解:原式=2
3×y0+1-1
(3)Sin245°+cos245
(sin30°)2+(cos30°
Sin 60
cos 60
tan 30
解:原式
+1
122
课前预习
领习新知
1.将下表填写完整
正弦值余弦值
正切值
30
45
60
当堂训练
巩固基础
知识点130°,45°,60角的三角函数值
(大庆)2cos60°的值为
B.√3
D
2.(无锡)sin45°的值为
B
B.
D
(天津)cOs30°的值为
A
D.√3
4.下列结论中正确的是
A.sin30°+sin40°=sin70
B.cos30+cos30°=cos60°
C.tan30°·tan60°=1
D. tan 30=tan 60
计算:
(1)2cos30°-tan45
(1-tan60°)2
解:原式=2
(2)3sin60°-√2cos45
解:原式
tan45—tan60
(3)sin30°·sin245°
sin30°
解:原式
知识点2根据特殊的三角函数值确定锐角的
度数
6.在Rt△ABC中,∠C=90°,若sinA
∠A的度数是
( A
C.60
若α为锐角,且tan(90°-a)=√3,则a为
A.30
B.45
C.60°
D,75°
8.在△ABC中,∠A,∠B都是锐角,且sinA
, COs
则△ABC的形状是(B
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
9.(本溪)在△ABC中,∠B=45°,cosA
∠C的度数是105
0.若3ana-2cos30°=0,则锐角a=30
1.若α为锐角,且sinα的值是方程2x2+3x
2=0的一个根,求a的度数及tana的值
解:由2x2+3x-2=0,得x1=-2
a为锐角,∴sina
a=30°..tana=tan30°
课后作业
全面提升
1.化简√(tan30°1)2等于
A
A.1
B.√3-1
D.√3+1
2.点M(-sin60°,-cos60°)关于x轴对称的点
的坐标是
B
D
212
3.在△ABC中,若sinA
tan b
0,则∠C的度数为
A.30°B.60°
C.90°
D,120°
4.已知a,B均为锐角,且满足sina
(tanB-1)2=0,则a+
计算:
(1)2cos230°-2sin60°·cos45
解:原式=2×
2×。Xy
(2)2sin60°-3tan30°
2019
解:原式=2
3×y0+1-1
(3)Sin245°+cos245
(sin30°)2+(cos30°
Sin 60
cos 60
tan 30
解:原式
+1
122
