【沪科版】数学九年级上册 第23章 专题六 求锐角三角函数值常用方法归类 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 第23章 专题六 求锐角三角函数值常用方法归类 习题课件 |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:09:24 | ||
图片预览




文档简介
(共19张PPT)
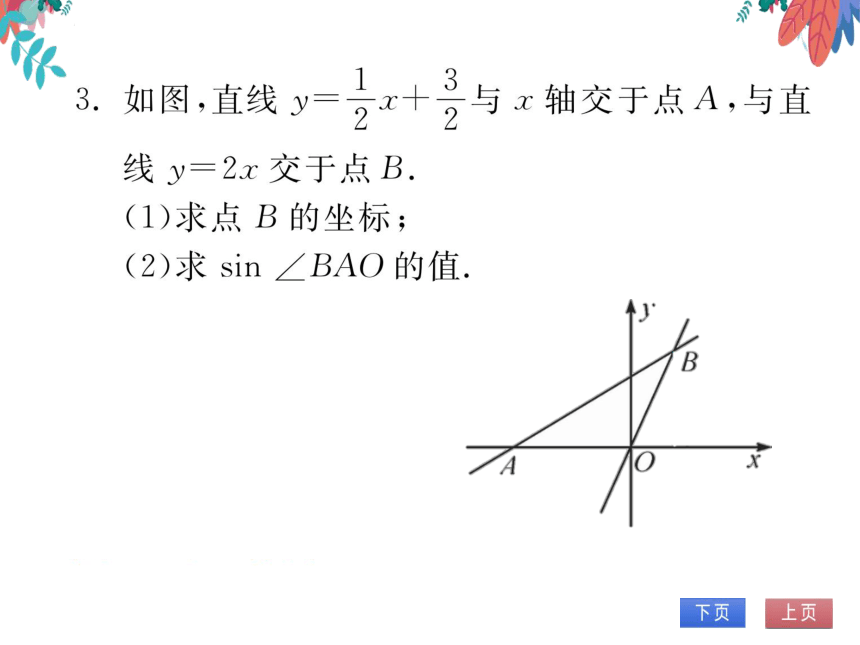
类型1运用定义求锐角三角函数值
如图,在Rt△ABC中,CD是斜边AB上的中
线,若CD=5,AC=6,则tanB的值是(
4
4
D
解:∴在Rt△ABD中,
tan∠ BAD- BD3
AD 4
BD=AD·tan∠BAD=9
CD=BC-BD=14-9=5
B
D
。A
AD2+CD2
122+52=13
AD 12
.. sin
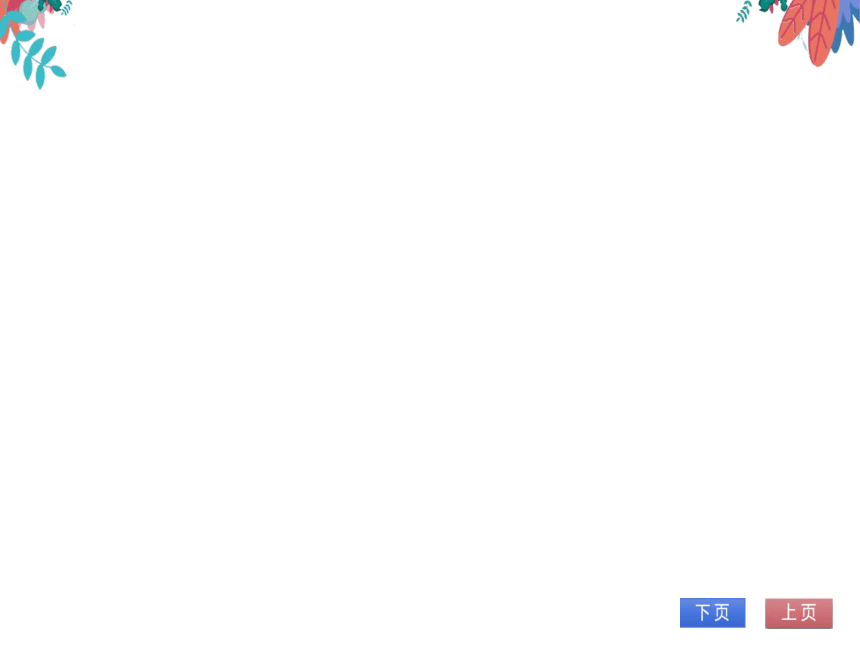
3.如图,直线
与x轴交于点A,与直
线y=2x交于点B
(1)求点B的坐标;
(2)求sin∠BAO的值
X
解:(1)解方程组
B
x+
y=2x
点B的坐标为(1,2)
(2)过点B作BC⊥x轴于点C
时,。x+
A(-3,0).∴OA=3.而OC=1,BC=2
∴AB=2√5..s
BAC Bc
AB
即sin∠BAO
类型2巧设参数求锐角三角函数值
4.在Rt△ABC中,∠C=90°,若sinA
tanB的值为
B
4
D
在△ABC中,∠C=90°,如果AC:BC=3:
4,那么sinA
已知a,b,c是△ABC的三边长,且t,b,c满足
b2=(c+a)(c-a).若5b-4c=0,求sinA
sinB的值
解:·b2=(c+a)(c-a),∴b2=c2-a2,即a2+
ABC是以c为斜边的Rt△ABC
6 4
5b-4c=0
设b=4k,则c=5k,∴在△ABC中,a=3k
b 3k 4k
sin asin B
+
k bk
解:设AE=x,则BE=3x,AM
BC=4x, AM=2x.CD=4C, E
EC=√(3x)2+(4x)2=5x,
EM=√x2+(2x)2
B
(2x)2+(4x)2
EM+CM2=CEZ
△CEM是直角三角形
sin∠ECM/EMN
类型3利用互余两角的三角函数的关系求锐角
三角函数值
8.在Rt△ABC中,∠C=90°,若sinA
COsB的值是
4
若α为锐角,且cosα
则sin(90°-a)等于
13
12
12
D
类型4利用等角求锐角三角函数值
0.如图,在△ABC中,AD⊥BC于点D,E为
AC的中点,如果AD=12,AB=15,BC=14
求tan∠ADE的值
解:AD⊥BC,
∠ADC=∠ADB=90°
E
点E为AC的中点
DE-AE=CEs I
AC. B
C
∠ADE=∠DAE
在Rt△ABD中,BD=AB=AD2=9,又
BC=14,CD=BC-BD=14-9=5
tan∠DAE=15
AD 12
tan∠ADE
类型1运用定义求锐角三角函数值
如图,在Rt△ABC中,CD是斜边AB上的中
线,若CD=5,AC=6,则tanB的值是(
4
4
D
解:∴在Rt△ABD中,
tan∠ BAD- BD3
AD 4
BD=AD·tan∠BAD=9
CD=BC-BD=14-9=5
B
D
。A
AD2+CD2
122+52=13
AD 12
.. sin
3.如图,直线
与x轴交于点A,与直
线y=2x交于点B
(1)求点B的坐标;
(2)求sin∠BAO的值
X
解:(1)解方程组
B
x+
y=2x
点B的坐标为(1,2)
(2)过点B作BC⊥x轴于点C
时,。x+
A(-3,0).∴OA=3.而OC=1,BC=2
∴AB=2√5..s
BAC Bc
AB
即sin∠BAO
类型2巧设参数求锐角三角函数值
4.在Rt△ABC中,∠C=90°,若sinA
tanB的值为
B
4
D
在△ABC中,∠C=90°,如果AC:BC=3:
4,那么sinA
已知a,b,c是△ABC的三边长,且t,b,c满足
b2=(c+a)(c-a).若5b-4c=0,求sinA
sinB的值
解:·b2=(c+a)(c-a),∴b2=c2-a2,即a2+
ABC是以c为斜边的Rt△ABC
6 4
5b-4c=0
设b=4k,则c=5k,∴在△ABC中,a=3k
b 3k 4k
sin asin B
+
k bk
解:设AE=x,则BE=3x,AM
BC=4x, AM=2x.CD=4C, E
EC=√(3x)2+(4x)2=5x,
EM=√x2+(2x)2
B
(2x)2+(4x)2
EM+CM2=CEZ
△CEM是直角三角形
sin∠ECM/EMN
类型3利用互余两角的三角函数的关系求锐角
三角函数值
8.在Rt△ABC中,∠C=90°,若sinA
COsB的值是
4
若α为锐角,且cosα
则sin(90°-a)等于
13
12
12
D
类型4利用等角求锐角三角函数值
0.如图,在△ABC中,AD⊥BC于点D,E为
AC的中点,如果AD=12,AB=15,BC=14
求tan∠ADE的值
解:AD⊥BC,
∠ADC=∠ADB=90°
E
点E为AC的中点
DE-AE=CEs I
AC. B
C
∠ADE=∠DAE
在Rt△ABD中,BD=AB=AD2=9,又
BC=14,CD=BC-BD=14-9=5
tan∠DAE=15
AD 12
tan∠ADE
