【沪科版】数学九年级上册 21.3 二次函数与一元二次方程 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 21.3 二次函数与一元二次方程 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
课前预习
预习新知
二次函数y=ax2+bx+c与一元二次方程ax2
bx+c=0的联系是:二次函数y=ax2+bx+c的
图象与x轴交点的横坐标x1,x2是一元二次方程
ax2+b+c=0的实数根,当b2-4ac>0时
二次函数y=ax2+bx+c的图象与x轴有两个
交点;当b-4c=0时,二次涵数y=ax2+bx+c的
图象与x轴有个交点;当b-4c<0时,二次
函数y=ax2+bx+c的图象与x轴没有交点
堂训练
巩固基础
知识点1二次函数与一元二次方程的关系
1.已知抛物线y=x2+ax+b与x轴的交点坐标
为(-2,0)和(-4,0),则方程x2+ax+b=0
的解为
4
抛物线y=x2-2x+1与坐标轴的交点情况为
B
A.两个交
C.无交点
D.三个交点
3.(锦州)二次函数y=ax2+bx
c(a≠0,a,b,c为常数)的图象
如图所示,ax2+bx+c=m有
实数根的条件是
B.m≥5
C.m≥0
72
4
知识点2用图象法求一元二次方程的近似解
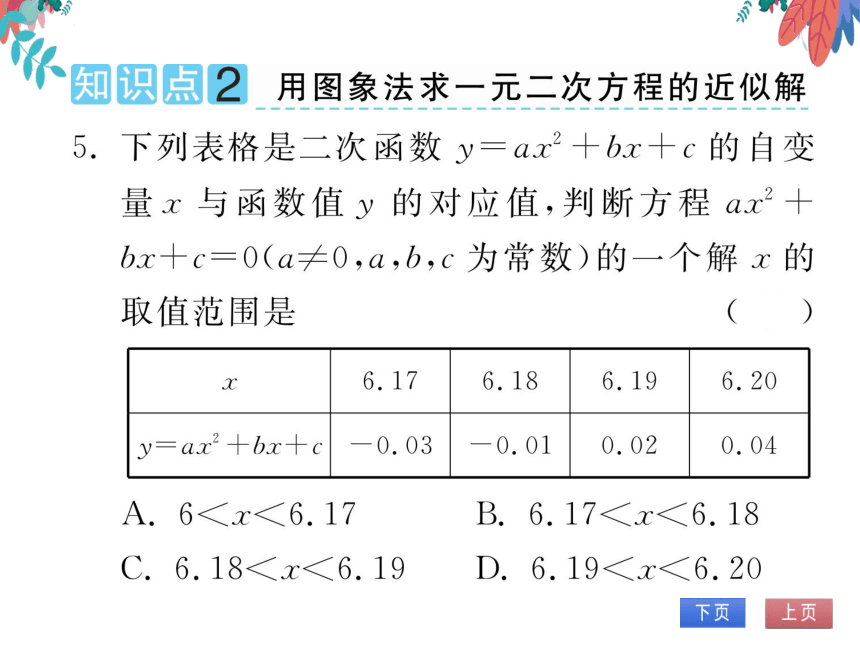
5.下列表格是二次函数y=ax2+bx+c的自变
量x与函数值y的对应值,判断方程ax2
bx+c=0(a≠0,a,b,c为常数)的一个解x的
取值范围是
6.17
6.20
axton
0.03
0.010.02
0.04
A.6B.6.179解
2x2-4x-1
画出抛物线y=2x2-4x-1的
图象如图所示
由图象知
当x≈2.2或x≈-0.2时,
即方程2x2-4x-1=0的近似解为x1≈2.2,
0.2
知识点3二次函数与一元二次不等式的关系
(黄石)二次函数y=ax2+bx+c(a≠0)的图
象如图所示,则函数值y>0时,x的取值范围
B.x>3
C.—13 x
(第7题图
8.如图是二次函数y=ax2+bx+c的部分图象
由图象可知不等式ax2+bx+c>0的解集是
B.x>5
C.x<-1且x>5D.x<-1或x>5
O 2
5\x
第8题图)
9.二次函数y=ax2+bx+c(a≠0)的图象如图
所示,根据图象解答下列问题:
2 4x
课后作业
全
提升
1.(徐州)若函数y=x2-2x+b的图象与坐标轴
有三个交点,则b的取值范围是
(A
A.b<1且b≠0
B.b>1
C.0D. b<
(东营)如果函数y=mx2+(m+2)x+2m
的图象与x轴只有一个交点,那么m的值为
B.0或2
C.2或-2
D.0,2或—2
课前预习
预习新知
二次函数y=ax2+bx+c与一元二次方程ax2
bx+c=0的联系是:二次函数y=ax2+bx+c的
图象与x轴交点的横坐标x1,x2是一元二次方程
ax2+b+c=0的实数根,当b2-4ac>0时
二次函数y=ax2+bx+c的图象与x轴有两个
交点;当b-4c=0时,二次涵数y=ax2+bx+c的
图象与x轴有个交点;当b-4c<0时,二次
函数y=ax2+bx+c的图象与x轴没有交点
堂训练
巩固基础
知识点1二次函数与一元二次方程的关系
1.已知抛物线y=x2+ax+b与x轴的交点坐标
为(-2,0)和(-4,0),则方程x2+ax+b=0
的解为
4
抛物线y=x2-2x+1与坐标轴的交点情况为
B
A.两个交
C.无交点
D.三个交点
3.(锦州)二次函数y=ax2+bx
c(a≠0,a,b,c为常数)的图象
如图所示,ax2+bx+c=m有
实数根的条件是
B.m≥5
C.m≥0
72
4
知识点2用图象法求一元二次方程的近似解
5.下列表格是二次函数y=ax2+bx+c的自变
量x与函数值y的对应值,判断方程ax2
bx+c=0(a≠0,a,b,c为常数)的一个解x的
取值范围是
6.17
6.20
axton
0.03
0.010.02
0.04
A.6
2x2-4x-1
画出抛物线y=2x2-4x-1的
图象如图所示
由图象知
当x≈2.2或x≈-0.2时,
即方程2x2-4x-1=0的近似解为x1≈2.2,
0.2
知识点3二次函数与一元二次不等式的关系
(黄石)二次函数y=ax2+bx+c(a≠0)的图
象如图所示,则函数值y>0时,x的取值范围
B.x>3
C.—1
(第7题图
8.如图是二次函数y=ax2+bx+c的部分图象
由图象可知不等式ax2+bx+c>0的解集是
B.x>5
C.x<-1且x>5D.x<-1或x>5
O 2
5\x
第8题图)
9.二次函数y=ax2+bx+c(a≠0)的图象如图
所示,根据图象解答下列问题:
2 4x
课后作业
全
提升
1.(徐州)若函数y=x2-2x+b的图象与坐标轴
有三个交点,则b的取值范围是
(A
A.b<1且b≠0
B.b>1
C.0
(东营)如果函数y=mx2+(m+2)x+2m
的图象与x轴只有一个交点,那么m的值为
B.0或2
C.2或-2
D.0,2或—2
