【沪科版】数学九年级上册 23.1.1 锐角的三角函数 第1课时 锐角的三角函数 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 23.1.1 锐角的三角函数 第1课时 锐角的三角函数 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第23章解直角三角形
23.1锐角的三角函数
1.锐角的三角函数
第1课时正切
课前预习
颍弓新知
1.在Rt△ABC中,∠C=90°,我们把锐角A的
对边与邻边的比叫做∠A的正切,记作
tanA,即tanA
∠A的对边
A的邻边
正切经常用来描述坡面的坡度,坡面的铅直
高度h和水平长度l的比叫做坡面的坡
度(或坡比),记作i,則
(或h2:l)
3.坡面与水平面的夹角叫做坡角(或称倾余
角),记作α,坡度与坡角的关系是
tan a
堂训练
巩固基础
知识点1正切
1.如图,在△ABC中,∠C=90°,AC=2,BC=1
则tanA等于
A
B.
D
B
(第1题图)
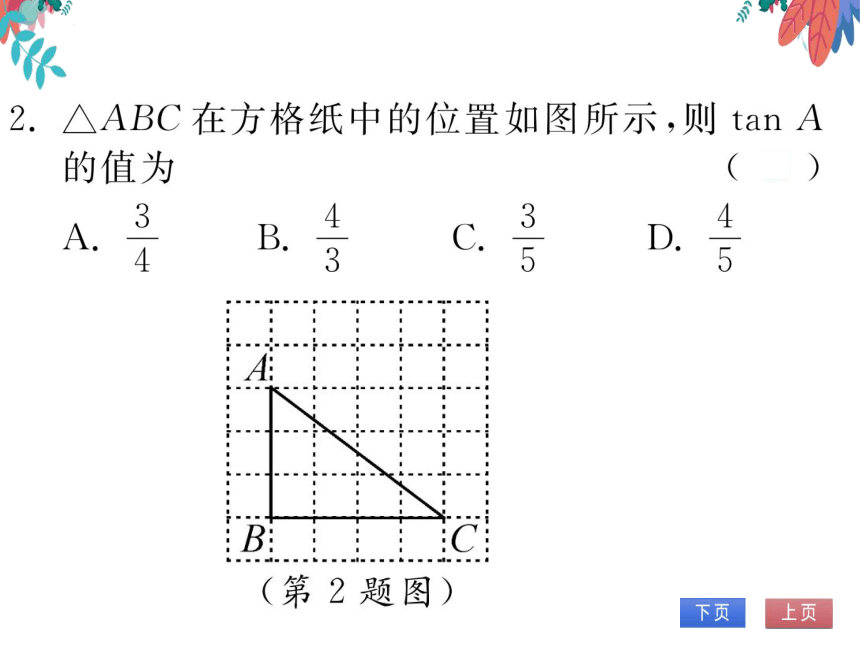
2.△ABC在方格纸中的位置如图所示,则tanA
的值为
B
4
4
D
B
(第2题图)
图,在△ABC
C=90°,AD是BC边上
的中线,BD=4,AD=2√5,则tan∠CAD的
值是
B
(第3题图)
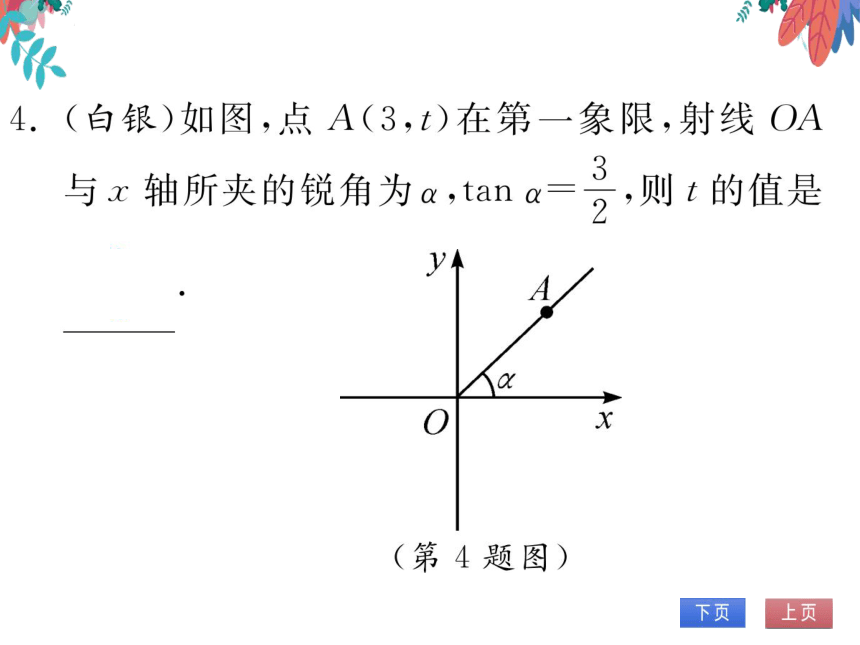
4.(白银)如图,点A(3,1)在第一象限,射线OA
与x轴所夹的锐角为a,tana
则t的值是
y
a
O
第4题图
图,在Rt△ABC中,∠ACB=90°,BC=6,
AB=10,求∠A,∠B的正切值
解:∴∠ACB=90°,
B
。AC
AB2-bc=8
bc 3
tan a
tan b
B
知识点2坡度与坡角
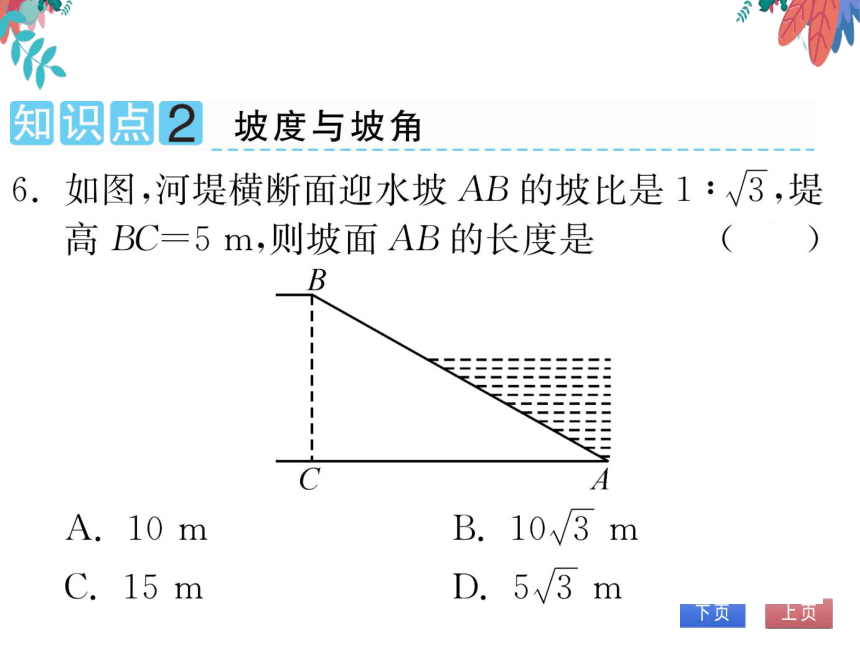
6.如图,河堤横断面迎水坡AB的坡比是1:√3,堤
高BC=5m,则坡面AB的长度是
(A
B
A.10
B.10
C.15m
D.5√3m
某商场内,电梯AB段的铅直高度与水平高度
如图所示,则电梯AB段的坡度i为
A.1:2
B.2:1
D.2:2√5
B
4
(第7题图)
B
h =2 m
第8题图)
课后作业
全面提升
1.(金华)在Rt△ABC中,∠C=90°,AB=5
BC=3,则tanA的值为
4
4
D
(贵阳)如图,A,B,C是小正方形的顶点,且每
个小正方形的边长均为1,则tan∠BAC的值
为
(兰州)如图,
坡长130m,坡顶离水平
地面的距离为50m,那么这个斜坡与水平地
面夹角的正切值等于
12
50m
题图)
4.如图,在坡屋顶的设计图中,AB=AC,屋顶的
宽度l为10m,坡角a为35,则坡屋顶的高度
h约为3.5m(参考数据:tan35°≈0.7,结
果精确到0.1m
h
B
(第4题图)
D
(第5题图)
6.(盐城)已知在△ABC中,tanB=,BC=6
过点A作BC边上的高,垂足为D,且满足
BD:CD=2:1,则△ABC面积的所有可能
值为8或24
第23章解直角三角形
23.1锐角的三角函数
1.锐角的三角函数
第1课时正切
课前预习
颍弓新知
1.在Rt△ABC中,∠C=90°,我们把锐角A的
对边与邻边的比叫做∠A的正切,记作
tanA,即tanA
∠A的对边
A的邻边
正切经常用来描述坡面的坡度,坡面的铅直
高度h和水平长度l的比叫做坡面的坡
度(或坡比),记作i,則
(或h2:l)
3.坡面与水平面的夹角叫做坡角(或称倾余
角),记作α,坡度与坡角的关系是
tan a
堂训练
巩固基础
知识点1正切
1.如图,在△ABC中,∠C=90°,AC=2,BC=1
则tanA等于
A
B.
D
B
(第1题图)
2.△ABC在方格纸中的位置如图所示,则tanA
的值为
B
4
4
D
B
(第2题图)
图,在△ABC
C=90°,AD是BC边上
的中线,BD=4,AD=2√5,则tan∠CAD的
值是
B
(第3题图)
4.(白银)如图,点A(3,1)在第一象限,射线OA
与x轴所夹的锐角为a,tana
则t的值是
y
a
O
第4题图
图,在Rt△ABC中,∠ACB=90°,BC=6,
AB=10,求∠A,∠B的正切值
解:∴∠ACB=90°,
B
。AC
AB2-bc=8
bc 3
tan a
tan b
B
知识点2坡度与坡角
6.如图,河堤横断面迎水坡AB的坡比是1:√3,堤
高BC=5m,则坡面AB的长度是
(A
B
A.10
B.10
C.15m
D.5√3m
某商场内,电梯AB段的铅直高度与水平高度
如图所示,则电梯AB段的坡度i为
A.1:2
B.2:1
D.2:2√5
B
4
(第7题图)
B
h =2 m
第8题图)
课后作业
全面提升
1.(金华)在Rt△ABC中,∠C=90°,AB=5
BC=3,则tanA的值为
4
4
D
(贵阳)如图,A,B,C是小正方形的顶点,且每
个小正方形的边长均为1,则tan∠BAC的值
为
(兰州)如图,
坡长130m,坡顶离水平
地面的距离为50m,那么这个斜坡与水平地
面夹角的正切值等于
12
50m
题图)
4.如图,在坡屋顶的设计图中,AB=AC,屋顶的
宽度l为10m,坡角a为35,则坡屋顶的高度
h约为3.5m(参考数据:tan35°≈0.7,结
果精确到0.1m
h
B
(第4题图)
D
(第5题图)
6.(盐城)已知在△ABC中,tanB=,BC=6
过点A作BC边上的高,垂足为D,且满足
BD:CD=2:1,则△ABC面积的所有可能
值为8或24
