【沪科版】数学九年级上册 23.1.1 锐角的三角函数 第2课时 正弦与余弦 习题课件
文档属性
| 名称 | 【沪科版】数学九年级上册 23.1.1 锐角的三角函数 第2课时 正弦与余弦 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
课前预习
颍习新知
在Rt△ABC中,∠C=90°,我们把锐角A的
对边与斜边的比叫做∠A的正弦,记
作sinA,即sinA
∠A的对边
斜边
我们把锐
角A的邻边与斜边的比叫做∠A的
余弦,记作cosA,即cosA
∠A的邻边
斜边
当堂训练
巩固基础
知识点1正弦
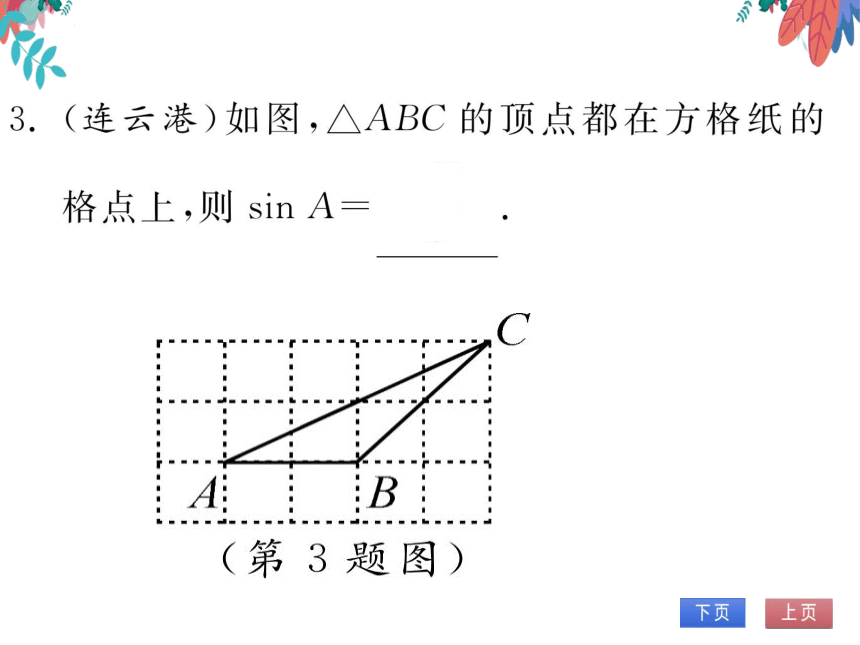
(温州)在Rt△ABC中,∠C=90°,AB=13
BC=5,则sinA等于
13
B.
D
2.如图,P是∠a的边OA上的一点,且点P的
坐标为(6,8),则sinα等于
4
B.
D
P(6,8
O
(第2题图)
知识点2余弦
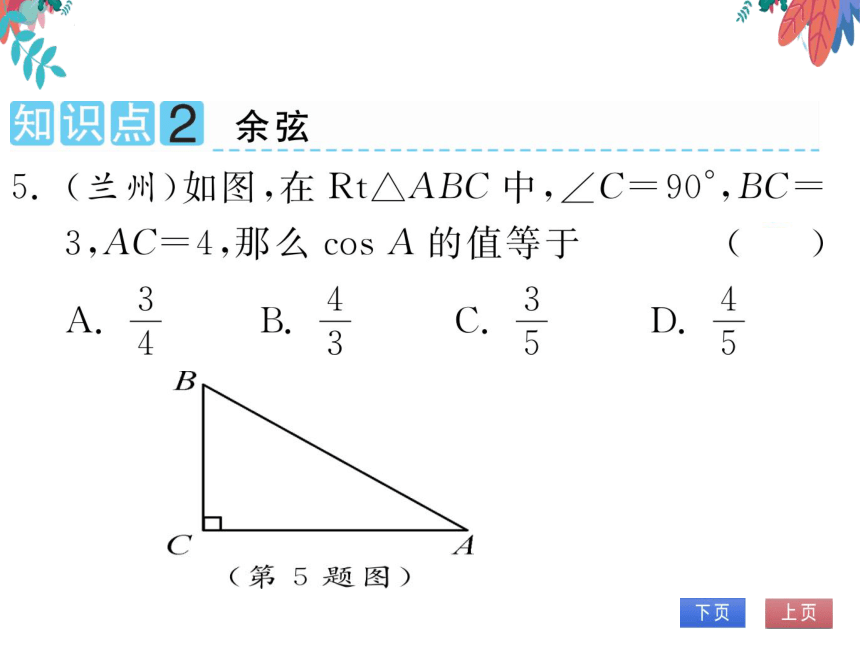
5.(兰州)如图,在Rt△ABC中,∠C=90°,BC
3,AC=4,那么cosA的值等于
D
4
A
D
B
(第5题图
如图,在平面直角坐标系中,已知点A(3,0)
点B(0,-4),则cos∠OAB等于
4
B.
D
A(3,0)
O
B(0,-4)
(第6题图)
图,已知在△ABC中,B
C=90°,AC=3,BC=2,
E
点D在边AC上,DE⊥AB,
垂足为E,则cos∠ADE的Ch
D
值是
13
知识点3锐角三角函数
8.在△ABC中,∠C=90°,AC=2,则AB的值为
a. 2sin a
B. 2cos A
D
coS
9.若α是锐角,sinα=3m-2,则m的取值范围
是
A.2B.2D. m
0.在Rt△ABC中,∠C=90°,BC=2,AC=1
现给出下列结论:①sinA
②cosB
5:tanA=2;④sinB
其中正确的
是②③(填序号).
1.如图,在△ABC中,∠C=90°,BC=3,AC
6,试求锐角A的各个三角函数
解
C=90
B
。AB
AC2+BC2=3
BC
Sin
AB
AC625
COS
AB
BC 1
tan a
课后作业
全面提升
1.(宜昌)亼ABC在网格中的位置如图所示(每
个小正方形的边长均为1),AD⊥BC于点D
下列选项中,错误的是
A
sin a- cos a
B. tan c=2
C. sin B=cos B
D. tan a=l
B
:D
第1题图)
2.(丽水)如图,两根竹笮AB和AD斜靠在墙
CE上,测得∠ABC=a,∠ADC=R,则竹竿
AB与AD的长度之比为
( B
tan a
Sin
tan
sin a
sin a
cos B
D
sin B
cos a
EDB
(第2题图
课前预习
颍习新知
在Rt△ABC中,∠C=90°,我们把锐角A的
对边与斜边的比叫做∠A的正弦,记
作sinA,即sinA
∠A的对边
斜边
我们把锐
角A的邻边与斜边的比叫做∠A的
余弦,记作cosA,即cosA
∠A的邻边
斜边
当堂训练
巩固基础
知识点1正弦
(温州)在Rt△ABC中,∠C=90°,AB=13
BC=5,则sinA等于
13
B.
D
2.如图,P是∠a的边OA上的一点,且点P的
坐标为(6,8),则sinα等于
4
B.
D
P(6,8
O
(第2题图)
知识点2余弦
5.(兰州)如图,在Rt△ABC中,∠C=90°,BC
3,AC=4,那么cosA的值等于
D
4
A
D
B
(第5题图
如图,在平面直角坐标系中,已知点A(3,0)
点B(0,-4),则cos∠OAB等于
4
B.
D
A(3,0)
O
B(0,-4)
(第6题图)
图,已知在△ABC中,B
C=90°,AC=3,BC=2,
E
点D在边AC上,DE⊥AB,
垂足为E,则cos∠ADE的Ch
D
值是
13
知识点3锐角三角函数
8.在△ABC中,∠C=90°,AC=2,则AB的值为
a. 2sin a
B. 2cos A
D
coS
9.若α是锐角,sinα=3m-2,则m的取值范围
是
A.2
0.在Rt△ABC中,∠C=90°,BC=2,AC=1
现给出下列结论:①sinA
②cosB
5:tanA=2;④sinB
其中正确的
是②③(填序号).
1.如图,在△ABC中,∠C=90°,BC=3,AC
6,试求锐角A的各个三角函数
解
C=90
B
。AB
AC2+BC2=3
BC
Sin
AB
AC625
COS
AB
BC 1
tan a
课后作业
全面提升
1.(宜昌)亼ABC在网格中的位置如图所示(每
个小正方形的边长均为1),AD⊥BC于点D
下列选项中,错误的是
A
sin a- cos a
B. tan c=2
C. sin B=cos B
D. tan a=l
B
:D
第1题图)
2.(丽水)如图,两根竹笮AB和AD斜靠在墙
CE上,测得∠ABC=a,∠ADC=R,则竹竿
AB与AD的长度之比为
( B
tan a
Sin
tan
sin a
sin a
cos B
D
sin B
cos a
EDB
(第2题图
